Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПРИЁМ И ОБРАБОТКА СИГНАЛОВ ОТ СЛОЖНЫХ ЦЕЛЕЙ

Доросинский Л. Г., Трухин М. П.,

2.1. Математическая модель цели и отражённого сигнала при решении задач распознавания пространственно-распределённых целей в космических РЛС с синтезированной апертурой

Радиолокационные станции бокового обзора с синтезированной апертурой (РСА), размещённые на космических носителях, обладают решающими преимуществами перед другими средствами космического наблюдения при решении задач классификации пространственно-распределённых объектов на земной и морской поверхностях и, в частности, незаменимы при космическом мониторинге акватории мирового океана. Космические РСА позволяют получить радиолокационные изображения (РЛИ) – радиолокационные портреты ПРЦ. На основе таких портретов формируются признаки для распознавания, использование которых обеспечивает достаточно высокую эффективность классификации ПРЦ.

Для решения проблемы синтеза оптимальных и квазиоптимальных алгоритмов формирования вектора достаточных статистик и, как следствие, получения признаков, используемых для классификации, предварительно должна быть записана математическая модель цели и модель отражённого сигнала, учитывающие особенности наблюдения цели и характеристик её движения.

Для описания взаимного расположения и перемещения носителей РЛС и наблюдаемой цели введем две системы координат (рис. 2.1): основную неподвижную систему 0XYZ и вспомогательную oxyz, связанную с геометрическими осями цели.

Для описания отражающих свойств наблюдаемых целей используем комплексную функцию отражения 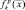k-й ПРЦ при наблюдении его р-й РЛС. В данном случае радиус-вектор элементарного отражающего участка (точки) во вспомогательной системе координат. При этом будем считать, что функция отражения имеет две независимые составляющие – диффузионную 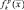, связанную с рассеянными отражениями от поверхности цели, и «зеркальную» 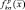, появление которой вызвано наличием зеркально отражающих элементов конструкции и элементов типа уголковых отражателей. Вторая компонента хорошо описывается совокупностью центров стабильного отражения, условно именуемых «блестящими точками», в то время как первая составляющая представляет собой
непрерывную функцию координат. Таким образом, для функции отражения может быть использовано следующее представление:

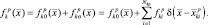(2.1.1)

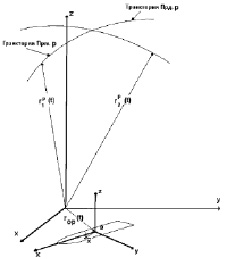
Рис. 2.1. Геометрические соотношения для р-й РЛС системы

В этом выражении 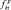 – значение комплексной функции отражения для i-й «блестящей точки» k-й цели при наблюдении ее р-й РЛС; Nkp – общее число «блестящих точек» при наблюдении цели k-го класса р-й РЛС;  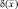– дельта-функция;  – радиус-вектор i-й «блестящей точки». Необходимо отметить, что вид функции отражения 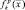существенным образом зависит от ракурса наблюдения цели, что не отмечено в (2.1.1) для сокращения записи. В тех случаях, когда зависимость характера отражений от ракурса имеет принципиальное значение для решения задачи синтеза и анализа алгоритмов распознавания, в контексте будут сделаны необходимые замечания.

При наблюдении цели несколькими (р) РЛС объединим функции отражения в р-компонентный вектор

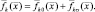(2.1.2)

Кратко остановимся на статистических свойствах функции отражения (2.1.2). Будем в дальнейшем считать, что диффузионная составляющая описывается р-мерным гауссовским функционалом плотности распределения вероятностей с нулевым вектором средних значений. Функции отражения соседних элементарных участков поверхности считаем статистически независимыми. При этом матрица взаимных корреляционных функций компонент вектора 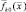может быть представлена в следующем виде:

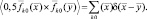(2.1.3)

Матрица 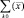в общем случае является эрмитовой, положительно определенной.

Если все РЛС системы работают независимо друг от друга, то эта матрица вырождается в вещественную диагональную. Этот случай, по-видимому, наиболее широко распространен в практически интересных ситуациях. Возможен другой крайний случай, когда все входящие в систему РЛС абсолютно когерентны. Такая ситуация может иметь место при работе всех станций от общей РЛС подсвета и достаточно близких ракурсах наблюдения. В этом случае 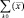вырождается в вещественную матрицу с равными элементами, что дает возможность представить ее в виде

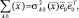(2.1.4)

где 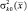 – распределение дисперсии диффузионной составляющей функции отражения по поверхности цели k-го класса;  – р-компонентный вектор-столбец, все элементы которого равны единице.

Для описания статистических свойств отраженных сигналов в литературе, как правило, используются три модели [1]:

– детерминированные отражения;

– для каждой «блестящей точки» амплитуда детерминирована, в то время как фаза случайна и равномерно распределена на интервале [–π, π];

– для каждой «блестящей точки» отраженный сигнал случаен и подчинен нормальному распределению плотности вероятности с нулевым математическим ожиданием.

При характерном для космических РСА времени наблюдения (менее 1 секунды) диффузионную составляющую можно считать квазидетерминированной, то есть случайной, но не изменяющейся за время наблюдения. Аналогичное предположение может быть высказано относительно функций отражения для «блестящих точек». При этом основным отличием «блестящих точек» от диффузионной составляющей функции отражения является их дискретный характер. Кроме того, суммарная ЭПР «блестящих точек» обычно предполагается много большей ЭПР поверхности цели и составляет до 80 % всей ЭПР цели [2]. Далее предполагаем, что функция отражения нормирована к суммарной ЭПР k-й цели таким образом, что выполняется равенство:

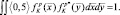(2.1.5)

Введем модель сигнала, принимаемого совокупностью РЛС. Будем считать радиолокационные станции, входящие в систему наблюдения, в общем случае бистатическими. Принимаемый отраженный сигнал представим в виде р-компонентного вектора комплексных амплитуд, для составляющих которого справедливо выражение:

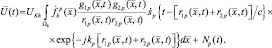(2.1.6)

В приведенном выражении 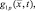 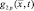– значения нормированных диаграмм направленности передающей и приемной антенн р-й РЛС в направлении точки цели в момент времени t; 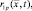 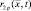– текущее значение дальности от передатчика и приемника р-й РЛС до точки цели; sp(t) – комплексная амплитуда модулирующей функции зондирующего сигнала р-й РЛС, которую в дальнейшем считаем импульсной с длительностью импульса τp и периодом повторения Тp и нормированной таким образом, что выполняется условие:

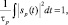(2.1.7)

Np(t) – комплексная амплитуда аддитивного шума радиолокационного тракта для р-й РЛС; kp = 2π / λ – волновое число.

Время наблюдения цели каждой РЛС системы ограничено и равно Тор.

С учетом нормировок (3.1.5) и (3.1.7) вещественный множитель Ukр имеет вид [3]:

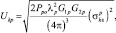(2.1.8)

где Рpo – импульсная мощность зондирующего сигнала р-й РЛС; G1p, G2p – коэффициент направленного действия (КНД) передающей и приемной антенн р-й РЛС; 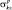 – суммарная ЭПР k-й цели при приеме сигнала р-й РЛС.

Введем диагональные матрицы размерности р×р:

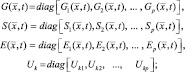(2.1.9)

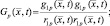(2.1.10)

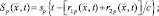(2.1.11)

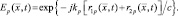(2.1.12)

Используя (2.1.2), вектор комплексных амплитуд принимаемых сигналов можно представить в виде суммы:

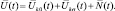(2.1.13)

В последнем выражении приняты следующие обозначения:

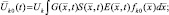(2.1.14)

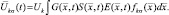(2.1.15)

Компоненты вектора комплексных амплитуд аддитивного шума радиолокационного тракта

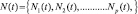(2.1.16)

будем считать гауссовскими белыми и статистически независимыми между собой. Вектор N(t) учитывает, как шумы приемников радиолокационных станций, так и сигналы, отраженные статистически однородной подстилающей поверхностью.

Из (2.1.6) следует, что для полного описания принимаемых сигналов необходимо в явном виде знать зависимость дальностей r1 и r2 от координат отражающей точки и текущего времени.

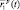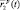На рис. 2.1 движения носителей передающей (Прд.р) и приемной (Прм.р) частей р-й РЛС описываются в основной системе координат 0XYZ радиус-векторами и . Движение центра масс наблюдаемой цели характеризуется радиус-вектором r(t) Для описания движения произвольной точки цели относительно центра масс в основной системе координат используем вектор 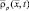. В произвольный момент времени t связь векторов 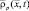и  задается выражением

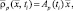(2.1.17)

где Ap(ti) – матрица поворота осей вспомогательной системы координат относительно основной системы 0XYZ в момент ti. Индекс «р» в приведенных выше обозначениях векторов соответствует порядковому номеру РЛС в системе и позволяет учесть не только отличия траекторий движения носителей РЛС, но и возможное изменение характера движения ПРЦ при наблюдении ее различными станциями системы на неперекрывающихся интервалах времени (например, одной РЛС при разных циклах обзора).

Без учета смещения носителей приемной и передающей частей РЛС за время распространения сигнала до цели и обратно искомые зависимости описываются выражениями:

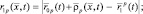(2.1.18)

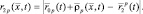(2.1.19)

Поскольку формулы (2.1.18) и (2.1.19) отличаются только индексами, то дальнейшие выкладки выполнены лишь для первой из них.

Разложим (2.1.18) в ряд Тейлора в окрестности точки t0p, соответствующей середине интервала наблюдения цели р-й РЛС

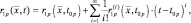(2.1.20)

здесь 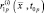 – значение i-й производной функции 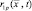по времени в момент t = t0p. Используя правила дифференцирования векторов и их модулей, получим выражения для первых четырех производных:

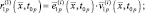(2.1.21)

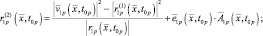(2.1.22)

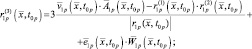(2.1.23)

(2.1.24)

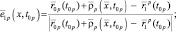(2.1.25)

– единичный вектор визирования точки в момент времени t,

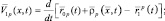(2.1.26)

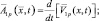(2.1.27)

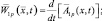(2.1.28)

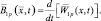(2.1.29)

Полученные соотношения достаточно компактны и при наличии данных о параметрах траекторий движения носителей РЛС и цели могут быть использованы для решения задач синтеза и анализа алгоритмов обнаружения, измерения параметров и классификации ПРЦ.