
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2. Многоальтернативная проверка гипотез относительно различных классов ПРЦ при их наблюдении совокупностью космических радиолокационных средств
Проблема определения класса цели может быть формализована в рамках классической теории многоальтернативной проверки статистических гипотез. По одной из них вектор принимаемых колебаний 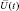 порожден только шумом. Остальные гипотезы соответствуют наблюдению на фоне шумов различных классов целей. Общее число возможных классов – М, число гипотез – (М + 1).
порожден только шумом. Остальные гипотезы соответствуют наблюдению на фоне шумов различных классов целей. Общее число возможных классов – М, число гипотез – (М + 1).
Если все существенные параметры (скорости движения РЛС и ПРЦ, координаты, ракурсы, распределения «блестящих точек» и диффузионной составляющей ЭПР по поверхности цели) точно известны для каждого из распознаваемых классов, то классическое решение задачи многоальтернативной проверки гипотез приводит к структуре устройства обработки принимаемых сигналов, состоящей из М параллельных каналов формирования отношения правдоподобия или его логарифма
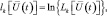
и решающего устройства, на М входов которого поступают значения lk. Решающее устройство выносит решение в пользу одной из М целей. Способ принятия решения зависит от выбранного критерия качества. При минимизации среднего риска процедура вынесения решения предусматривает проверку системы линейных неравенств, учитывающих априорные вероятности и конкретный вид матрицы потерь. При использовании критерия максимального правдоподобия решение выносится в пользу гипотезы с максимальным значением lk. В любом случае наибольший практический интерес представляет процедура формирования отношения правдоподобия и структурная схема устройства, реализующего это отношение.
Достаточная статистика для принятия решения представляет собой вектор, составленный из отношений правдоподобия для каждой из М конкурирующих гипотез. Логарифм отношения правдоподобия для k-й гипотезы при отсутствии флуктуаций сигналов, отраженных «блестящими точками», может быть записан в виде [4]:
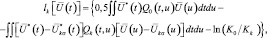 (2.2.1)
(2.2.1)
где K0 и Kk – нормирующие коэффициенты функционалов плотности распределения вероятностей для случаев наблюдения только шума и k-й цели на фоне шума; Q0(t,u), Qk(t,u) – комплексные матрицы, обратные матрицам взаимной корреляции принимаемого вектора 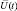 для гипотез о наблюдении только шума R(t,u) и k-й цели на фоне шума Rk(t,u).
для гипотез о наблюдении только шума R(t,u) и k-й цели на фоне шума Rk(t,u).
Поскольку шум и диффузионная составляющая принимаемого сигнала 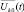 являются независимыми случайными процессами, то
являются независимыми случайными процессами, то
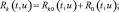 (2.2.2)
(2.2.2)
где 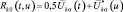 (2.2.3)
(2.2.3)
– матрица корреляционных функций диффузионных составляющих вектора принимаемого сигнала.
Для определения вида матриц Q0(t,u) и Qk(t,u) следует воспользоваться интегрально-матричными уравнениями обращения:
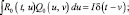 (2.2.4)
(2.2.4)
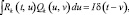 (2.2.5)
(2.2.5)
где I – единичная диагональная матрица.
Для последнего слагаемого в (2.2.1) справедливо равенство:
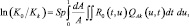 (2.2.6)
(2.2.6)
где QAk(u,t) – решение интегрально-матричного уравнения:
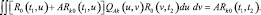 (2.2.7)
(2.2.7)
При условии, что шум радиолокационного тракта «белый» с диагональной матрицей спектральных плотностей N0 выражения (2.2.4)–(2.2.7) упрощаются:
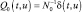 ; (2.2.8)
; (2.2.8)
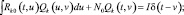 (2.2.9)
(2.2.9)
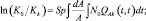 (2.2.10)
(2.2.10)
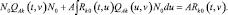 (2.2.11)
(2.2.11)
Пользуясь рекомендациями [4], ищем матрицу Qk(t,u) в виде
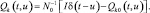 (2.2.12)
(2.2.12)
В этом случае равенство (2.9) преобразуется следующим образом:
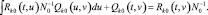 (2.2.13)
(2.2.13)
Сравнение (2.2.11) с (2.2.13) показывает, что матрица Qk0(t,u) может быть найдена путем решения (2.2.11) при А = 1, т. е.
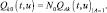 (2.2.14)
(2.2.14)
Подставляя (2.2.8) в (2.2.1), получим:
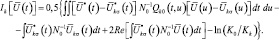 (2.2.15)
(2.2.15)
Последнее выражение позволяет представить один из возможных вариантов структуры устройства формирования логарифма отношения правдоподобия для k-й гипотезы (рис. 2.2). Из (2.2.15) и рис. 2.2 следует, что основу устройства формирования 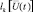 составляют два корреляционных канала. В одном из них вычисляется корреляция принимаемой реализации вектора
составляют два корреляционных канала. В одном из них вычисляется корреляция принимаемой реализации вектора 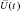 , нормированного к мощности шумов, с вектором ожидаемого сигнала, порожденного «блестящими точками» k-й цели
, нормированного к мощности шумов, с вектором ожидаемого сигнала, порожденного «блестящими точками» k-й цели 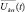 . Во втором канале разностный сигнал
. Во втором канале разностный сигнал 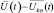 коррелируется с вектором
коррелируется с вектором
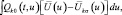
который представляет собой оценку диффузионной составляющей принимаемого сигнала в предположении о наблюдении k-й цели.
Дальнейшая конкретизация алгоритма формирования логарифма отношения правдоподобия и структуры реализующего его устройства возможна лишь при определении матриц QAk(t,u) и Qko(t,u), для чего необходимо решить уравнение (2.2.11). Прежде всего выясним вид корреляционной функции Rk0(t,u). Используя (2.2.14) и (2.2.3), получим:
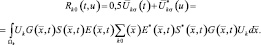 (2.2.16)
(2.2.16)
Воспользовавшись широко известным приемом [5], будем искать QAk(t,u) в виде, аналогичном (2.2.16):
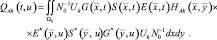 (2.2.17)
(2.2.17)
После подстановки (2.2.16), (2.2.17) уравнение (2.2.11) может быть представлено в виде
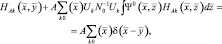 (2.2.18)
(2.2.18)
где введена матрица (p×p)
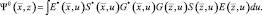 (2.2.19)
(2.2.19)
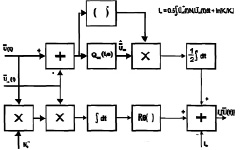
Рис. 2.2. Вариант структурной схемы устройства формирования
логарифма отношения правдоподобия
Подстановка (2.2.17) в (2.2.15) дает следующий результат:
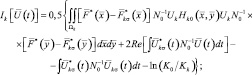 (2.2.20)
(2.2.20)
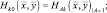 (2.2.21)
(2.2.21)
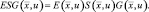 (2.2.23)
(2.2.23)
Используя (2.2.15), преобразуем второе и третье слагаемые в фигурных скобках (2.2.20). В результате получим:
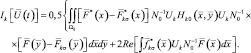 (2.2.24)
(2.2.24)
Кратко рассмотрим смысл введенных функций 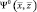 ,
, 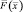
и 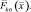
Поскольку произведение
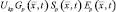
представляет собой траекторный сигнал, принимаемый р-й РЛС от точечной цели с координатой  , то диагональные элементы матрицы
, то диагональные элементы матрицы 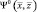 следует трактовать как нормированные к
следует трактовать как нормированные к 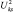 функции неопределенности траекторного сигнала соответствующих РЛС.
функции неопределенности траекторного сигнала соответствующих РЛС.
Рассмотрим р-ю компоненту вектора 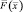 . При отсутствии шума с учетом (2.2.6) имеем:
. При отсутствии шума с учетом (2.2.6) имеем:
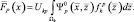 (2.2.25)
(2.2.25)
Как следует из полученного выражения, при отсутствии аддитивных шумов функция 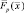 с точностью, зависящей только от функции неопределенности
с точностью, зависящей только от функции неопределенности 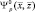 траекторного сигнала для р-й РЛС, восстанавливает функцию отражения наблюдаемой цели. Функцию
траекторного сигнала для р-й РЛС, восстанавливает функцию отражения наблюдаемой цели. Функцию 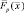 будем называть комплексным радиолокационным изображением объекта наблюдения, получаемым по данным р-й РЛС. Компоненты вектора
будем называть комплексным радиолокационным изображением объекта наблюдения, получаемым по данным р-й РЛС. Компоненты вектора 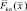 следует рассматривать как изображения, порожденные только совокупностью «блестящих точек» цели k-го класса без учета шумов и диффузионной составляющей: отраженного сигнала.
следует рассматривать как изображения, порожденные только совокупностью «блестящих точек» цели k-го класса без учета шумов и диффузионной составляющей: отраженного сигнала.
Полученные выражения (2.2.22)–(2.2.24) дают возможность представить структуру устройства формирования логарифма отношения правдоподобия в виде, отличном от ранее описанного (см. рис. 2.3.). При этом вся обработка может быть разделена на два этапа. На первом этапе вектор принимаемых сигналов 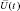 преобразуется в вектор комплексных РЛИ наблюдаемой цели. Поскольку матрицы, используемые для этого преобразования, являются диагональными, перекрестные связи между РЛС системы на этом этапе отсутствуют. На втором этапе элементы вектора комплексных РЛИ нормируются к спектральным плотностям аддитивных шумов и обрабатываются в соответствии с алгоритмом (2.2.24).
преобразуется в вектор комплексных РЛИ наблюдаемой цели. Поскольку матрицы, используемые для этого преобразования, являются диагональными, перекрестные связи между РЛС системы на этом этапе отсутствуют. На втором этапе элементы вектора комплексных РЛИ нормируются к спектральным плотностям аддитивных шумов и обрабатываются в соответствии с алгоритмом (2.2.24).
Для выяснения физического смысла интеграла
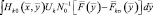
умножим его слева на
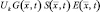
и проинтегрируем результат по  . Учитывая (2.2.14) и (2.2.17), получим:
. Учитывая (2.2.14) и (2.2.17), получим:
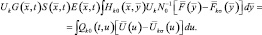 (2.2.26)
(2.2.26)
Как уже отмечалось, правая часть (2.2.26) представляет собой оценку диффузионной составляющей принимаемого сигнала в предположении о наблюдении k-й цели. Используя (2.2.14), представим эту оценку в виде:
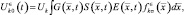 (2.2.27)
(2.2.27)
составляющей функции отражения k-й цели по координатам. Сравнение (2.2.26) и (2.2.27) приводит к следующему результату:
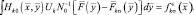 (2.2.28)
(2.2.28)
Таким образом, рассматриваемый интеграл дает оценку диффузионной составляющей функции отражения наблюдаемой цели в предположении о принадлежности ее к k-й гипотезе.
Выполненный синтез показывает, что в случае отсутствия флуктуации сигналов, отраженных «блестящими точками», для вычисления логарифмов отношения правдоподобия, наряду с принимаемыми реализациями сигнала могут и должны быть использованы комплексные РЛИ наблюдаемых целей. При этом обработка изображения заключается в вычислении корреляций его с детерминированной функцией отражения «блестящих точек» k-й цели 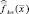 и оценкой диффузионной составляющей
и оценкой диффузионной составляющей 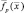 .
.
Реализация подобной системы представляется чрезвычайно сложной, в первую очередь, из-за очень высоких требований к качеству и объему априорных сведений.
Для реализации оптимальной обработки требуется знание числа, координат на поверхности цели и значений ЭПР каждой «блестящей точки», входящей в радиолокационный портрет ПРЦ, при всех значениях ракурса его наблюдения, параметрах качки, рыскания, взаимного расположения и характеристик взаимного перемещения цели и космического аппарата. Названная информация должна быть известна для каждой РЛС, входящей в состав комплекса наблюдения.
Для каждой ПРЦ необходимо знание распределения диффузионной составляющей отражений по координатам его поверхности при всех перечисленных выше условиях.
Получение подобной информации принципиально недостижимо в обозримом будущем, что ставит на повестку дня разработку алгоритмов обработки в максимальной мере сочетающих теоретическую базу оптимального синтеза, приведенного выше, с теми априорными данными, которыми уже располагает разработчик системы классификации и которые могут быть получены в результате обозримых в будущем экспериментов, опытной и рабочей эксплуатации средств классификации целей.
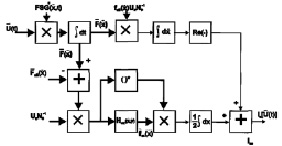
Рис. 2.3. Вариант структурной схемы устройства формирования
логарифма отношения правдоподобия
К устойчивым и достоверным сведениям о различиях распознаваемых пространственно-распределённых целей могут быть отнесены:
а) данные о различиях в размерах (длине и ширине);
б) данные о различиях в интегральной (общей) ЭПР.
Индивидуальные отличия по характеристикам отражения для отдельных целей, как правило, имеют очень ограниченный характер – единичные радиолокационные портреты (РП) при незначительном числе параметров наблюдения, что исключает возможность создания сколько-нибудь достоверных статистически усредненных баз данных. В связи с этим рабочий алгоритм классификации должен структурно опираться на названные выше достоверные сведения, быть адаптивным, а именно содержать возможность настройки на пополняющиеся априорные данные и параметры, характеризующие каждую конкретную ситуацию наблюдения (оценки ракурса, направления и скорости перемещения цели и других параметров её движения).
Принимая во внимания высказанные соображения, рабочий алгоритм формирования статистик принятия решения не должен требовать индивидуальных радиолокационных портретов (распределения ЭПР «блестящих точек» и диффузионной составляющей по поверхности цели). Считая распределение ЭПР равномерным, приходим к следующему выражению статистики, которая составляет основу принятия решения по любому статистическому критерию
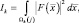 (2.2.29)
(2.2.29)
где подчеркнута зависимость области, занятой целью k-го класса от ракурса его наблюдения φ.
Из последнего выражения, в частности, следует, что основными признаками классификации являются оценки области поверхности, занятой целью, то есть по существу оценки его длины и ширины при данном ракурсе, а также оценка интегральной ЭПР отраженного сигнала.
