Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПРИЁМ И ОБРАБОТКА СИГНАЛОВ ОТ СЛОЖНЫХ ЦЕЛЕЙ

Доросинский Л. Г., Трухин М. П.,

2.4. Адаптивный алгоритм классификации пространственно-распределённых целей по данным радиолокатора с синтезированной апертурой

Рассмотрим ситуацию, когда необходимо принимать решение о принадлежности объекта к одному из трех классов (большой, маленький, средний). В общем случае принципиально возможно разделение объектов на большее число классов. Однако, как методология построения алгоритмов классификации, так и их содержание при увеличении числа классов останутся качественно неизменными, если не считать естественных количественных отличий.

Решение задачи распознавания ПРЦ усложняется в связи с наличием амплитудных флюктуаций наблюдаемого радиолокационного портрета ПРЦ, зависимостью его параметров от условий наблюдения: ракурса, отношения сигнал/шум, состояния подстилающей поверхности, определяющей ее удельную ЭПР и уровень АРУ сигнала, а также угловых скоростей перемещения цели. Вращательное движение цели с априорно неизвестными скоростями вызывает сложные искажения его РЛИ, проявляющиеся в сжатии (растяжении) его изображения вдоль путевой дальности, в кажущемся изменении ракурса цели и взаимного расположения отдельных блестящих точек.

Указанные особенности задачи приводят к тому, что алгоритмы классификации должны базироваться на процедуре адаптивного обучения, в процессе которой формируются эталоны классов объектов и зависимости их характеристик от различных параметров, прежде всего от ракурса.

Для получения и обоснования алгоритмов обработки радиолокационных изображений с целью выделения классификационных признаков и алгоритмов собственно классификации кораблей приведем краткий вывод оптимального алгоритма с тем, чтобы путем аргументированных его упрощений обосновать методологию получения рабочих алгоритмов для классификации.

Решение этой проблемы в общем виде произведем при следующих предположениях:

1. РСА перемещается по прямолинейной траектории, использует импульсный широкополосный зондирующий сигнал, причем отсчеты РЛИ различных каналов дальности могут считаться статистически независимыми. В связи с этим все дальнейшие рассуждения проводятся для одного канала дальности. Обобщение алгоритма на все РЛИ производится естественным образом на заключительном этапе вывода алгоритма классификации.

2. Весь участок поверхности, попадающий в один канал дальности, разбит на отдельные элементарные участки, состоящие, в свою очередь,
из большого числа элементарных отражателей. Каждый элементарный участок определяется своей координатой di (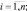 n – число таких участков) по отношению к центру всей наблюдаемой поверхности. Сигнал, отраженный от такого участка, представляет собой нормальный случайный процесс с нулевым математическим ожиданием и дисперсией 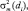которая зависит от целого ряда параметров, в первую очередь, от типа объекта и индивидуальных особенностей его архитектуры, дальности и ракурса его наблюдения и т. п. При обозначении мощности отраженного сигнала сохранен индекс «m», характеризующий ее зависимость от номера класса объекта.

3. Сигналы, отраженные различными элементарными участками поверхности, созданы физически различными отражателями и поэтому с достаточным основанием могут считаться статистически независимыми.

4. В качестве достаточной статистики, являющейся методологической основой, как выбора признаков, так и алгоритма принятия решения, будет использовано отношение правдоподобия для гипотез о классе объектов.

С учетом принятых предположений комплексная амплитуда сигнала, принимаемого в n-й точке траектории от i-го элементарного участка поверхности цели и/или близлежащей точки подстилающей поверхности с координатой xi может быть записана в следующем виде:

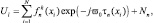(2.4.1)

где ϖ0 – несущая частота; τn(xi) – запаздывание сигнала, принимаемого в n-й точке траектории от i-го элементарного участка наблюдаемой поверхности; 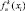 – комплексная амплитуда сигнала, формируемого i-м элементарным участком поверхности объекта k-го класса в n-й точке приема; Nn – комплексная амплитуда n-го отсчёта шума. Комплексная амплитуда представляет собой выборочное значение нормальной случайной величины, имеющей следующие статистические характеристики:

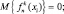(2.4.2)

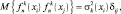(2.4.3)

где δij – символ Кронеккера.

Обозначая расстояние до центра наблюдаемого участка поверхности RH, запишем величину запаздывания отраженного сигнала от i-го элементарного участка до n-й точки траектории:

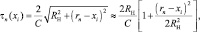(2.4.4)

где C – скорость света; rn – координата n-й точки приема отраженного сигнала.

Обобщая высказанные предположения, сформируем вектор наблюдаемых данных на выходе приемника локатора:

U = βf k + Nщ, (2.4.5)

где β = (S(xi), ..., S(xn)) – матрица (NИ×n), состоящая из векторов:

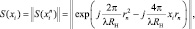(2.4.6)

задающих фазовое распределение сигнала, отраженного от i-го элемента поверхности, по точкам синтезируемой апертуры, имеющим координаты rn (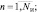 NИ – число принимаемых импульсов);  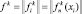– вектор комплексных амплитуд, размерность которого определяется числом отражающих элементарных участков поверхности; Nш – вектор отсчетов шума, имеющего следующие статистические характеристики: 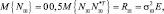где E – единичная матрица,
а 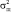 – дисперсия шума.

Для решения задачи классификации по какому-либо из статистических критериев: минимума среднего риска, максимума апостериорной плотности или максимального правдоподобия (этот критерий в дальнейшем будет принят в качестве основного) – необходимо записать отношение правдоподобия:

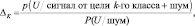(2.4.7)

где P[U/.] – условная плотность вероятности наблюдения вектора U при наличии поверхности k-го класса и шума или только шума. Считая вектор U гауссовским с нулевым математическим ожиданием, что соответствует предыдущим рассуждениям, запишем отношение правдоподобия:

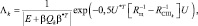(2.4.8)

где 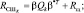(2.4.9)

– матрица мощностей сигналов от каждого из n элементарных участков, входящих в анализируемую поверхность k-го класса.

Учитывая специальный вид матрицы (2.4.9) и используя равенство Вудбери, запишем логарифм отношения правдоподобия в следующем виде:

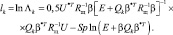(2.4.10)

Здесь

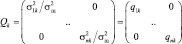(2.4.11)

– диагональная матрица отношений мощностей сигналов от каждого i-го элементарного участка к мощности шума в одном импульсе.

Вводя новый вектор

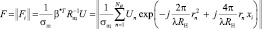, (2.4.12)

компоненты которого представляют собой отсчеты комплексных амплитуд РЛИ, для достаточной статистики (логарифма отношения правдоподобия) получаем выражение:

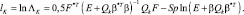(2.4.13)

Считая размер элементарного участка поверхности равным размеру элемента разрешения по азимуту и пренебрегая влиянием соседних участков 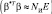, получаем выражение достаточной статистики:

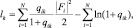(2.4.14)

где qik(i = 1, ..., N; k = 1, ..., M) – отношение сигнал/шум в i-м элементе разрешения после когерентного накопления N отсчетов; М – число классов.

При известных априори «радиолокационных портретах» (векторах qik,) для каждого из классифицируемых типов поверхностей оптимальный алгоритм классификации состоит в том, чтобы вычислить достаточную статистику для каждого возможного m и выбрать максимальное значение.

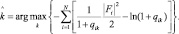(2.4.15)

К сожалению, подробные «радиолокационные портреты» (РП), как правило, неизвестны практически ни для одной ПРЦ, что приводит к необходимости их оценки на этапе предварительного обучения. Соответственно алгоритм классификации имеет вид:

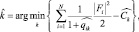(2.4.16)

где знак «уголок над символом» обозначает оценку соответствующего параметра на этапе предварительного обучения.

Следует обратить особое внимание на тот факт, что достоверная оценка РП представляет собой очень сложную в организационном и вычислительном плане задачу, в первую очередь, из-за чрезвычайно большого объема факторов, влияющих на вид радиолокационного портрета. К таким факторам можно отнести зависимость РП от условий наблюдения (дальность, ракурс, длина волны, поляризация), погодных и климатических условий, времени суток и времени года, индивидуальных особенностей, конфигурации и электродинамических свойств наблюдаемых объектов. В то же время, очевидно, что в любом случае основой для решения задачи классификации является вектор достаточных статистик

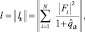(2.4.17)

Этот вектор является основой для принятия решения в решающем пространстве, так как константы 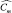не зависят от наблюдаемых данных. Использование этого вектора представляет основу для классификации ПРЦ. Его следует применять на практике во все более возрастающей степени по мере создания банка радиолокационных портретов, полученных в разных условиях наблюдения.

Поскольку на этапе эскизного проектирования говорить о наличии представительного банка РП безусловно преждевременно, для синтеза алгоритма классификации приходится использовать те исходные данные о различии объектов, которые не вызывают сомнений и имеют ясное физическое обоснование. Такими робастными признаками, как показано выше, являются размеры и общая ЭПР ПРЦ, в то время как индивидуальные (присущие конкретному кораблю) признаки, содержащиеся в РП ПРЦ, на этом этапе априори не известны. В тех случаях, когда какие-либо надежные сведения о распределении ЭПР по поверхности цели отсутствуют, целесообразно считать такое распределение равномерным с тем, чтобы ориентироваться на худшую ситуацию, ибо наличие
индивидуальных особенностей, отличающих один класс от другого, не может, по крайней мере, потенциально ухудшить эффективность распознавания.

В этом случае при формировании весовых коэффициентов βmi не используется информация о «тонкой» структуре РП, но учитываются априорные сведения об отличии классов объектов по размерам и ориентации областей, занимаемых «портретами» ПРЦ на РЛИ. Названные области, в свою очередь, существенно зависят от условий наблюдения, в частности, оценок наклонной дальности и ракурса.

В этом случае компоненты вектора a вычисляются путем суммирования отсчетов РЛИ в пределах области, зависящей, как от номера конкурирующей гипотезы. так и от ракурса наблюдения ПРЦ:

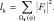(2.4.18)

Более подробно алгоритм выглядит следующим образом.

По наблюдаемому РЛИ, предъявленному к классификации, прежде всего, производятся две операции:

– оценка области, занятой элементами цели на изображении, например, путем сравнения отсчетов с порогом, установленным по уровню шума;

– оценка ракурс , использующая только те отсчеты РЛИ, которые отнесены к ПРЦ по результатам предыдущей пороговой обработки.

Поскольку размерность вектора равна числу конкурирующих гипотез, при обучении необходимо моделировать Т выборочных векторов 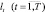при задании объектов каждого из M классов, расположенных под ракурсом, величина которого оценивается по наблюдаемому РЛИ

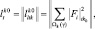(2.4.19)

где 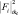 – i-й отсчет t-й обучающей выборки при условии, что объект относится к классу k0. Следует обратить внимание на отличие индексов k и k0. Первый из них – координата вектора, а второй – номер объекта, для которой производится моделирование выборочных отсчетов РЛИ 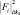на этом этапе обучения.

В результате обучения формируются оценки векторов выборочных средних:

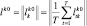(2.4.20)

и выборочных дисперсий:

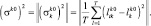(2.4.21)

Принятие решения производится по минимуму расстояния:

(2.4.22)

Анализ алгоритмов распознавания ПРЦ, различающихся удельной ЭПР или размерами, приведен методом статистического моделирования в главе 3.

Принятая методология опирается на понятие достаточной статистики, поскольку вектор достаточных статистик является оптимальным набором признаков, позволяющим решить задачу классификации наилучшим образом в рамках критерия минимума среднего риска. В то же время формирование названного вектора наталкивается на практически непреодолимые трудности из-за очень большой априорной неопределённости. В связи с этим целесообразно искать признаки классификации, начиная с вектора достаточных статистик путём его последовательного упрощения путём отказа от тех деталей и тонких особенностей, которые недоступны классификатору в условиях реальной работы.

Отражающие свойства цели моделируются комплексной функцией отражения, имеющей две составляющих. Одна из них описывает диффузионное отражение радиосигналов от поверхности ПРЦ и является непрерывной функцией координат поверхности цели, а вторая составляющая вызвана наличием в конструкции цели центров интенсивного отражения электромагнитных воле, которая хорошо аппроксимируется совокупностью «блестящих» точек. Диффузионная составляющая предполагается гауссовской с нулевым математическим ожиданием. Значения функций отражения от «блестящих» точек также считаются гауссовскими и независимыми между собой.

Основные результаты раздела заключаются в следующем.

Для заданной модели отражающих свойств ПРЦ на основе байесовского подхода решена задача многоальтернативной проверки гипотез применительно к наблюдению пространственно-распределённых целей системой космических РЛС. При этом предполагалось, что приём осуществляется на фоне аддитивного гауссовского шума и закон движения наблюдаемой цели известен. Получено выражение для элементов вектора достаточных статистик, представляющих собой логарифмы отношений правдоподобия для всех возможных классов целей. Предложена структурная схема устройства, обеспечивающего формирование достаточных статистик.

Показано, что формирование вектора признаков должно осуществляться в два этапа:

1. По данным каждой РЛС, входящей в систему, методом искусственного синтезирования апертуры формируется радиолокационное изображение наблюдаемой цели.

2. Вектор полученных РЛИ обрабатывается таким образом, чтобы сформировать вектор достаточных статистик. Формирование достаточной статистики осуществляется с помощью двухканального устройства. В одном канале формируется логарифм отношения правдоподобия для диффузионной составляющей сигнала, отражённого k-й целью, на фоне шума. Второй канал вычисляет логарифм отношения правдоподобия для сигнала, отражённого «блестящими» точками k-й цели, на фоне шума и диффузной отражающей сигнала.