Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.3.1. Проблема анализа эффективности алгоритмов классификации
Сложившаяся практика решения задачи классификации ПРЦ предполагает, что процедура синтезирования искусственной апертуры антенны выполнена в результате первичной обработки радиолокационного сигнала, а распознающему автомату предъявляются данные в виде отдельных отсчетов с выхода устройства детектирования, иначе говоря, в виде отсчетов радиолокационного изображения или выборочного радиолокационного портрета ПРЦ.
В качестве основного метода классификации, разумно сочетающего близость к оптимальному с относительно простой технической реализацией, может быть использован следующий алгоритм принятия решения о классе ПРЦ, предложенный в главе 2. В качестве решения принимается гипотеза о классе с номером 
, для которого выполняется соотношение:
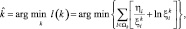(3.3.1)
где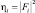 
– i-й отсчет РЛИ наблюдаемого ПРЦ; 
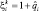– i-й отсчет ожидаемого значения ЭПР (радиолокационного портрета) цели k-го класса.
В результате сравнения статистик l(k) указывается номер 
класса ПРЦ, принимаемого за истинный. Выбранный алгоритм базируется на предположении о статистической независимости отдельных отсчетов РЛИ ηi и их принадлежности к экспоненциальным распределениям (если распределение входной реализации гауссовское с нулевым математическим ожиданием) с параметрами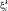 
, зависящими от номера класса ПРЦ. Суммирование в (3.3.1) производится по области Ωk, которая, в свою очередь, так же определяется предполагаемым классом цели.
Анализ точности классификации заключается в расчете вероятностей ошибочных и истинных решений о классах наблюдаемых ПРЦ. Вероятность принятия решения о справедливости k-й гипотезы при условии, что истинна 1-я, определяется выражением:
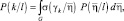(3.3.2)
где G – пространство решений;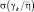 
– правило решения; 
– вектор принимаемых данных; (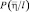
– плотность распределения принимаемых данных при условии, что истинна гипотеза «1».
Производя замену переменных и выбирая в качестве новой переменной функцию
yk = l(k), (3.3.3)
приходим к записи выражения для вероятности ошибки в виде многомерного интеграла от совместного распределения статистик у1....уN по той области пространства решений, которая соответствует k-й гипотезе:
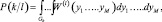(3.3.4)
где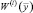 
– совместная плотность распределения случайных величин у1...уM при условии, что принимается 1-я гипотеза; М – общее число принимаемых гипотез; Gk – область пространства решений, соответствующая принятию k-й гипотезы.
В рассматриваемом случае пределы интегрирования в выражении для вероятности принятия решения о наличии цели k-го класса при наблюдении цели 1-го класса могут быть конкретизированы:
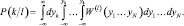(3.3.5)
Плотность распределения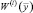 
выражается через значения отсчетов РЛИ с помощью формулы:
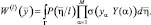(3.3.6)
С учетом независимости компонент вектора наблюдений 
плотность вероятности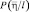 
имеет вид:
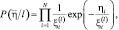(3.3.7)
где N – размерность вектора наблюдений 
.
Определим σ – функцию, входящую в (3.3.5), следующим образом:
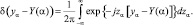
Подставляя (3.3.2) в (3.3.7) и (3.3.6) в (3.3.5), получим:
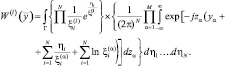(3.3.8)
После замены переменных:
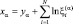(3.3.9)
определим характеристическую функцию, соответствующую плотности распределения
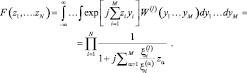(3.3.10)
Для определения плотности вероятности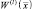 
найдем обратное преобразование Фурье от последнего выражения (3.3.10):
(3.3.11)
Вычисление полученного интеграла приводит к чрезвычайно громоздким результатам. И тем не менее эти вычисления следовало бы привести при том условии, что полученные выражения носили бы конструктивный характер, а именно позволяли бы рассчитать вероятности ошибочных решений.
Поэтому рассмотрим вначале частный случай, при котором вычисление (3.3.11) тривиально и убедимся в степени продуктивности полученного решения для анализа эффективности распознавания в целом.
Допустим, что размерность вектора наблюдений, равная N, совпадает с числом конкурирующих гипотез М. На практике обычно выполняется неравенство N > М. Тем не менее, такое предположение не лишено целесообразности. Оно приводит к расширению числа классов ПРЦ – появлению подклассов в пределах каждого класса, что делает задачу анализа эффективности классификации более детальной. После расчета вероятностей ошибок, если, разумеется, такой расчет удастся осуществить аналитическими методами, результаты можно «загрубить», объединяя вероятности ошибочных решений внутри подкласса.
После замены переменных:
(3.3.12)
или в матричной записи:
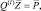
где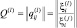 
(3.3.13)
и предположения о том, что матрица Q – неособенная, перепишем формулу (3.3.11):
(3.3.14)
В последнем выражении приняты следующие обозначения:
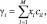(3.3.15)
где, в свою очередь, cil – элемент матрицы:
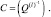(3.3.16)
Интегралы, стоящие в (3.3.14), легко вычисляются, и выражение для плотности вероятности принимает вид:
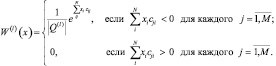(3.3.17)
Подставив (3.3.17) в выражение (3.3.5), получим формулу для расчета вероятностей ошибок:
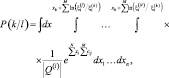(3.3.18)
при условии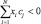 
для каждого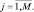 
Вычисление последнего интеграла аналитическими методами представляет собой непреодолимую задачу, что, в частности подтверждается аналогичными выводами, проделанными в [104]. Общий случай (М ≠ N) еще более сложен. В связи с этим особое внимание должно быть уделено приближенным методам вычисления вероятностей ошибок, к рассмотрению которых мы переходим в следующих параграфах. Безусловно, особый интерес для анализа алгоритма классификации представляет метод статистического моделирования, который и с формальной точки зрения является одним из наиболее мощных методов вычисления многомерных интегралов. Этот метод будет использован при анализе информативности геометрических и «моментовых» признаков.