Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПРИЁМ И ОБРАБОТКА СИГНАЛОВ ОТ СЛОЖНЫХ ЦЕЛЕЙ

Доросинский Л. Г., Трухин М. П.,

3.3.2. Вывод расчетных выражений для оценки вероятностей правильных и ошибочных решений при классификации ПРЦ по РЛИ

Рассмотрим приближенный метод [7] определения вероятностей правильных и ошибочных выборов гипотез о классах ПРЦ. Алгоритм проверки гипотез принимает решение об истинности класса ПРЦ, если соответствующее ему значение статистики:

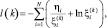(3.3.19)

основанной на модели плотности вероятности наблюдаемого вектора (3.3.7), принимает максимальное значение.

Для выходной статистики, построенной в предположении, что ПРЦ соответствует k-му классу при условии, что на самом деле вектор наблюдаемых данных соответствует 1-му классу, введем обозначение l(I)(k).

Ошибка классификации имеет место в том случае, когда при наблюдении РЛИ ПРЦ 1-го класса выносится решение в пользу ПРЦ k-го класса. Такая ситуация наступает, если выходной эффект, соответствующий k-й гипотезе l(I)(k), оказывается больше, чем выходной эффект, соответствующий истинной гипотезе l:

lI(k) > lI(l). (3.3.20)

Вероятность этого события определяется выражением:

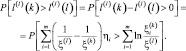(3.3.21)

В общем случае формула для вероятности правильного решения может быть записана следующим образом:

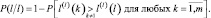(3.3.22)

Поскольку выходной эффект l(I)(k) может превышать статистику l(I)(l) при нескольких значениях k (события совместны), точный расчет вероятностей в правой части (3.3.22) довольно сложен (формально эта процедура не отличается от описанной в предыдущем параграфе). Однако, используя только вероятности (3.3.21), удается записать выражение для нижней границы вероятности правильного решения:

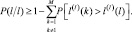(3.3.23)

Следует иметь в виду, что с повышением точности классификации нижняя граница вероятности правильного решения (3.3.23) приближается к истинному значению вероятности. Действительно, чем выше эффективность устройства классификации, тем меньше вероятность события, заключающегося в том, что выходные эффекты, соответствующие двум и более ложным гипотезам, будут превышать статистику (3.3.19), соответствующую наблюдению истинной цели. Приведенное заключение имеет тем больше оснований, чем меньше число конкурирующих гипотез, что соответствует рассматриваемой ситуации классификации ПРЦ.

Введем обозначения:

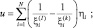(3.3.24)

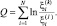(3.3.25)

причем 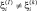(в противном случае отсчеты конкурирующих РЛИ не отличаются и соответствующе значения ЭПР исключаются из рассмотрения),

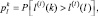(3.3.26)

где 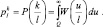(3.3.27)

В (3.3.27) функция W(u/l) представляет собой плотность распределения вероятностей случайной величины u, определенной из (3.3.24), при условии, что случайные величины ηi, как это следует из исходной постановки задачи, имеют плотность распределения вероятностей:

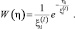(3.3.28)

Характеристическая функция, соответствующая распределению (3.3.28), имеет вид:

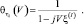(3.3.29)

Обозначив

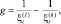(3.3.30)

найдем характеристическую функцию величины gi ηi:

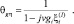(3.3.31)

Характеристическая функция для u определяется как характеристическая функция суммы независимых случайных величин:

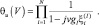(3.3.32)

Преобразовав (3.3.32) по Фурье, находим плотность вероятности:

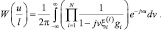(3.3.33)

Обозначим

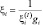(3.3.34)

и перепишем выражение(3.3.33):

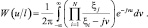(3.3.35)

Для вычисления полученного интеграла (3.3.35) рассмотрим типовые практически важные ситуации и примем ряд предположений. Будем считать, что каждое из распознаваемых РЛИ: 1-е и k-е в общем случае содержат 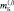(j = 1, M) отсчетов, вызванных наличием «блестящих» точек, 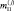(j = 1, M) отсчетов, определяющихся диффузионными отражениями от распределённой поверхности ПРЦ и  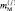(j = 1, M) отсчетов от подстилающей поверхности. Отсчеты от «блестящих» точек на каждом из РЛИ отличаются по величине ЭПР как между собой, так и между отсчетами от «блестящих» точек, распределённой и подстилающей поверхности на «своем» и конкурирующем РЛИ. Иначе ведут себя отсчеты, соответствующие распределённой поверхности: в пределах «своего» РЛИ они не отличаются по величине ЭПР и, следовательно, отличаются от отсчетов распределённой поверхности другого РЛИ на постоянную величину. Относительно подстилающей поверхности могут быть высказаны аналогичные соображения. Из сказанного следует, что при наличии mКП отсчетов распределённой поверхности на одинаковых позициях двух РЛИ такова же кратность полюсов подынтегрального выражения. Если число элементов двух РЛИ, имеющих одинаковые расположения и «занятых» МП, равно mКМ, то в подынтегральном выражении столько же одинаковых полюсов, разумеется, отличающихся по значению от «полюсов подстилающей поверхности».

При выполнении принятых предположений вычислим интеграл (3.3.35):

при u > 0, (3.3.36)

где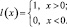

В выражении (3.3.36) суммирование производится лишь по тем индексам, для которых ζq > 0 (q ∈ MБ, причем MБ – множество тех позиций 1-го и k-го РЛИ, на которых расположены «блестящие точки», другими словами, множество некратных полюсов.

При u < 0 интеграл (3.3.35) выглядит аналогично.

(3.3.37)

В последнем выражении суммирование производится лишь по тем индексам, для которых ζi < 0.

После подстановки (3.3.36) и (3.3.37) в (3.3.27) найдем формулу для вычисления вероятности превышения ложным выходным эффектом истинного.

а) при Q > 0:

(3.3.38)

где r – номера тех индексов, для которых ζq > 0;

б) при Q < 0:

(3.3.39)

Вычисления по приведенным формулам неоправданно громоздки и могут быть существенно упрощены в соответствии со следующими предположениями:

а) размер фрагмента РЛИ выбирается таким образом, чтобы не превышать максимальных размеров РЛИ ПРЦ, что заведомо ограничивает возможное число отсчетов, приходящихся на подстилающую поверхность;

б) отношение сигнал/фон в каждом элементе разрешения, содержащем отсчеты, принадлежащие цели, для реальных РЛИ составляет не менее 10 дБ;

в) в «блестящих» точках РЛИ ПРЦ сосредоточено, по крайней мере, 80 % ее ЭПР.

Высказанные предположения позволяют отказаться от учета отсчетов, соответствующих распределённой и подстилающей поверхностям на конкурирующих РЛИ. Очевидно, что следствием такого условия будет некоторое увеличение вероятностей ошибок и снижение нижней границы вероятности правильной классификации, что, естественно, приведет к несколько заниженным оценкам качества распознавания. При этом в формулах (3.3.38) и (3.3.39) будут отсутствовать два последних слагаемых: именно в таком варианте они могут быть использованы для анализа эффективности классификации при задании ЭПР ПРЦ в виде совокупности «блестящих» точек, распределенных по поверхности цели. При этом расчетная формула для определения вероятности правильной классификации ПРЦ k-го класса выглядит следующим образом:

при Q > 0

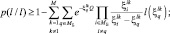
при Q < 0

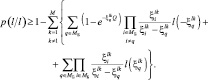(3.3.40)

В выражении (3.3.40) приняты следующие обозначения:

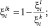
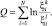
Рассмотренный выше метод анализа предполагает наличие априорной информации о числе, ЭПР и распределении «блестящих» точек по координатам поверхности ПРЦ. Количество такой информации существенно ограничено в связи с явно недостаточным объемом экспериментальных данных, натурного и полунатурного моделирования. Из сказанного следует, что как построение алгоритмов распознавания, так и соответствующий анализ следует производить исходя из существенно более простых моделей РЛИ, учитывающих лишь безусловно присутствующие объективные отличия между распознаваемыми классами, к которым относятся различия в размерах и ЭПР.

Поскольку в этом случае индивидуальные особенности радиолокационных портретов ПРЦ не учитываются, оценки вероятностей правильной и ложной классификации будут ниже истинных, что не приведет к излишне оптимистическим выводам об эффективности классификации.

Предположим, что РЛИ ПРЦ k-го класса представляет собой совокупность nk экспоненциально распределенных независимых отсчетов, принадлежащих цели, и, соответственно, m – nk отсчетов, созданных только шумом, причем, «целевые» отсчеты имеют одинаковую между собой ЭПР, равную σk/nk (σk – интегральная ЭПР цели k-го класса, а параметр экспоненциального распределения «шумовых» отсчетов равен σШ.

В этом случае оптимальный алгоритм классификации может быть синтезирован по критерию максимального правдоподобия, в соответствии с которым решения принимается в пользу той гипотезы, для которой отношение правдоподобия максимально:

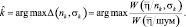(3.3.41)

где 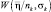 – плотность вероятности вектора наблюдаемых данных при наличии цели k-го класса; 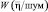 – плотность вероятности вектора наблюдаемых данных при наличии только шума.

При экспоненциальном распределении вероятностей отсчетов РЛИ отношение правдоподобия может быть записано в следующем виде:

(3.3.42)

где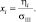

Вероятность принятия k-й гипотезы при истинной гипотезе с номером 1 находится из условия:

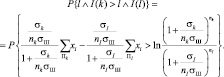(3.3.43)

В рассматриваемой ситуации гипотезы могут быть упорядочены следующим образом: с возрастанием номера гипотезы как размеры ПРЦ, так и ее интегральная ЭПР уменьшаются, то есть при K > 1 считаем, что nk < nI и наоборот. Введем обозначения:

при k > l (nI > nk),

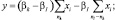(3.3.44)

при k < l (nk > nl),

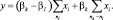
Поскольку справедливой считается 1-я гипотеза, в случае «а» плотность вероятности случайной величины xi равна

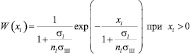(3.3.45)

в первой и второй суммах, а в случае «б» плотность вероятности в первой сумме определяется в соответствии с выражением (3.3.45), а во второй сумме:

W(xi) = exp(–xi).

После определения характеристической функции и плотности вероятности случайной величины у найдем расчетные выражения для вероятностей ошибочных и верных решений относительно принятия k-й гипотезы при истинной гипотезе с номером 1.

При k > l; 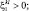Q > 0:

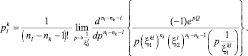
При k > l; 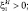Q < 0:

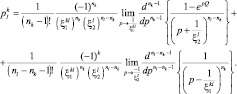
При k > l; 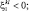Q > 0:

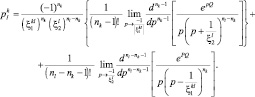
При k > l; 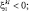Q < 0:

Результат – предыдущая формула при Q = 0.

При k < l; 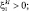Q > 0:

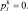
При k < l; 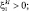Q < 0:

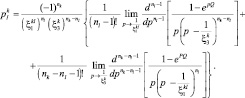
При k < l; 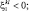Q > 0:

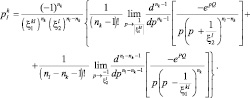
При k < l; 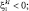Q < 0:

(3.3.46)

При записи выражения (3.3.46) использованы следующие обозначения:

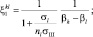
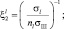
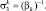
Существенного упрощения вычислений можно достичь при условии, что количество слагаемых в первой и второй суммах выражения (3.3.44) достаточно велико, чтобы считать справедливым предположение о нормализации случайной величины у. В этом случае статистика (3.3.44) гауссова и имеет следующие параметры.

При k > 1

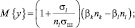
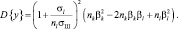
При k < 1

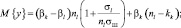
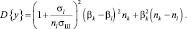
Оценки вероятностей ошибочных и верных решений находится из очевидного соотношения:

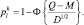
Приведенная методика позволяет рассчитать оценки вероятностей правильного решения о классификации ПРЦ при самых различных радиолокационных портретах – распределениях ЭПР по поверхности ПРЦ. В то же время расчеты могут оказаться неоправданно (для приближенной методики) сложными, если в составе радиолокационных портретов ПРЦ присутствует достаточно большое количество точек с одинаковыми (близкими) значениями ЭПР. В этом случае представляется целесообразным использовать несколько иную методику расчета, описанную ниже.