Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.7. Методика расчета вероятности правильного распознавания при объединении решений отдельных СН методом простого голосования
Рассмотрим задачу расчета матрицы вероятностей правильных и ошибочных решений при условии, что частные решения выносятся одинаковыми средствами наблюдения методом простого голосования. Число объединяемых решений Р. Априорные вероятности Рj наблюдения каждого типа ПРЦ известны. Число классов, как и в предыдущих случаях, равно трем. Предположим, что в пользу j-го класса принято nj частных решений. Общее число объединяемых решений – N. Тогда вероятность возникновения конкретной ситуации совмещения n1, n2 и n3 = N – (n1 + n2) частных решений при наблюдении цели 1-го класса равна
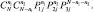
Следует заметить, что при использовании простого голосования могут возникнуть конфликтные ситуации, когда справедливо одно из следующих условий
n1 = n2 > n3;
n1 = n3 > n2; (3.7.1)
n2 = n3 > n1
или n1 = n2 = n3 = N/3. (3.7.2)
Предположим, что разрешение конфликтных ситуаций производится случайным образом. При этом в ситуациях (3.7.1) конфликт между j-м и r-м классами разрешается в пользу j-го класса с вероятностями Рk2 (j/r), которые представлены в виде матрицы:
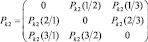
для элементов которой справедливо условие
Pk2(j/r) + Pk2(r/j) = 1 при j ≠ r.
Конфликтные ситуации типа (3.7.1) с вероятностью PKЭ(j) разрешаются в пользу j-ro класса. При этом справедливо равенство
Pk3(1) + Pk3(2) + Pk3(3) = 1.
Используя введенные предположения, для вероятности вынесения итогового решения в пользу j-гo класса при наблюдении цели i-го класса можно воспользоваться выражением:
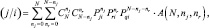
где r ≠ j, r ≠ q, q ≠ j.
Коэффициент A(N, nj, nr) принимает следующие значения:
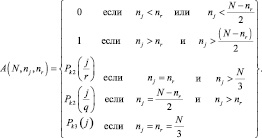
Вероятность правильного распознавания ПРЦ на основе частных решений определяется в соответствии с выражением