Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.1.2. Анализ эффективности алгоритма измерения координаты центра ПРЦ
Оценка максимума апостериорной вероятности образуется путем выбора канала формирования 
(хЦ), в котором апостериорная плотность вероятности принимает максимальное значение. В частности, если известно приближение 
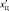к истинному значению хЦ, отстоящее от последнего меньше, чем на величину апостериорного среднеквадратичного разброса, удобно аппроксимировать 
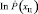квадратичным разложением относительно точки 
:
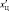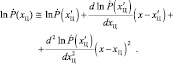(4.1.21)
После дифференцирования по хЦ получаем решение уравнение правдоподобия
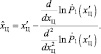(4.1.22)
При относительно невысокой априорной точности, когда априорное распределение практически неизменно в окрестности пика коэффициента правдоподобия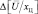 
, переходим к оценкам максимального правдоподобия. При этом дисперсия оценки определяется соотношением
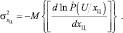(4.1.23)
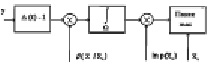
Рис. 4.1. Блок-схема измерителя координаты центра (поток Пуассона)
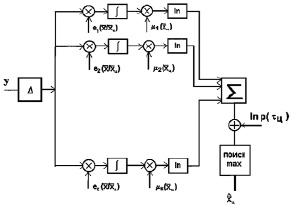
Рис. 4.2. Блок-схема измерителя координаты центра (поток Бернулли)
Применяя известную методику расчета дисперсии оценки [1], при аппроксимации последовательности отметок от цели пуассоновским потоком получим для нее следующее выражение:
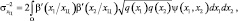(4.1.24)
где q(x) – отношение сигнал/шум, заданное как функция от координат цели; ψ(х1, х2) – функция неопределенности, определяемая в соответствии с соотношением (3.3.19).
Дальнейшую конкретизацию выражения (4.1.24) проведем при следующих предположениях:
1) отношение сигнал/шум не зависит от координат цели, а необходимые энергетические соотношения учтены при определении интенсивности потока β(х), которая, в свою очередь, представляет собой симметричную функцию;
2) оцениваемый общегрупповой параметр хЦ представляет собой координату центра интенсивности β(х).
Для получения простых выражений, позволяющих произвести предварительную оценку эффективности определения общегруппового центра цели рассмотрим два частных случая.
1. При достаточно высоком разрешении воспользуемся аппроксимацией функции неопределенности
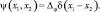(4.1.25)
Тогда:
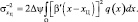(4.1.26)
При постоянном значении отношения сигнал/шум: р = const
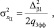(4.1.27)
где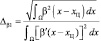 
(4.1.28)
– эффективная протяженность групповой цели;
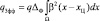(4.1.29)
– эффективное общегрупповое отношение сигнал/шум.
2. В этом примере используем гауссовские функции для аппроксимации интенсивности потока и сигнальной функции (при вычислении функции неопределенности):
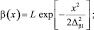(4.1.30)
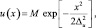(4.1.31)
где коэффициенты L и М определяются из условий нормировки:
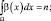(4.1.32)
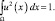(4.1.33)
После подстановки последних выражений в (4.1.24) получим:
(4.1.34)
Минимум дисперсии оценки достигается при условии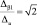 
и равен
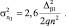(4.1.35)
Несмотря на частный характер последних соотношений, можно сделать вывод достаточно общего характера: при определении центра группы мало связанных между собой слабых сигналов целесообразно иметь средство наблюдения с разрешающей способностью, сравнимой по размерам с эффективным размером группы. В практически важных случаях, связанных с классификацией ПРЦ, когда требуемая разрешающая способность существенно выше, оптимальный алгоритм определения центра формирует «стробы», «загрубляющие» разрешение до требуемой величины.
При использовании для моделирования отсчетов сигнала от цели в виде потока Бернулли для дисперсии оценки координаты центра получим аналогичное выражение
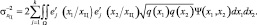(4.1.36)
Предположим, что внутригрупповые сигналы могут находиться только на вполне определенных позициях, то есть:
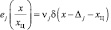(4.1.37)
и считая ψ(x1, x2) = ψ(x1 – x2), получим:
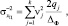(4.1.38)
где ΔФ – ширина интервала разрешения; qj – отношение сигнал/шум в j-м интервале разрешения.
Формула (4.1.38) отражает в основном те же качественные особенности измерения общегруппового центра, что и при использовании потока Пуассона. Точность растет при увеличении отношения сигнал/шум и среднего числа элементарных целей. В то же время дисперсия увеличивается при увеличении числа элементов разрешения, приходящихся на размер групповой цели (при увеличении отношения протяженности цели к величине элемента разрешения).