Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.2. Оценка области, занимаемой целью на РЛИ
Выделение области, занимаемой радиолокационным портретом ПРЦ на РЛИ, представляет собой известную задачу сегментации, методам решения которой посвящен ряд работ, в частности, [3–12, 13]. Традиционные алгоритмы сегментации реализуют такие методы, как пространственное дифференцирование, функциональная аппроксимация, высокочастотная фильтрация, пороговая обработка, двумерная линейная фильтрация и т. д. Практическое применение рассматриваемых методов в задаче распознавания ПРЦ на борту КА вряд ли осуществимо, в первую очередь, из-за их вычислительной сложности, с одной стороны, и из-за необходимости экспериментального подбора параметров (настройки алгоритмов с помощью оператора), с другой. Существенный недостаток традиционных алгоритмов – недостаточное внимание к принципиальной необходимости учета флуктуации РЛИ ПРЦ, а также к формализации методов анализа их эффективности и результатам такого анализа.
Указанные недостатки могут быть преодолены при разработке алгоритма сегментации на основе статистической модели РЛИ с использованием аппарата и методологии теории статистических решений.
Хорошей моделью для РЛИ в РСА с достаточно высоким разрешением может служить двумерное поле независимых отсчетов мощности отраженного сигнала, одномерные плотности вероятности которых отличаются для отсчетов, соответствующих отражениям от фона и от поверхности ПРЦ. В первом приближении примем допущение о том, что все отсчеты фона имеют плотность вероятности WФ(Uij), а цели – WЦ(Uij). В этом случае оптимальный алгоритм оценивания области, занимаемой отсчетами цели, записанный по критерию максимального правдоподобия, будет иметь вид:
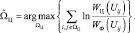(4.2.1)
Реализация алгоритма (4.2.1) является чрезвычайно трудоемкой из-за необходимости перебора всех возможных границ области, внутри которой расположена цель. Однако, с учетом статистической независимости сигналов в отдельных каналах дальности, максимум выражения в фигурных скобках (4.2.1) может быть получен, если максимизировать каждое отдельное слагаемое
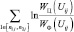(4.2.2)
для каждого канала дальности с номером j (n1j и n2j – граничные точки, разделяющие область фона и цели в j-м канале дальности). Таким образом, оптимальный алгоритм определения области, занимаемой целью, сводится к оптимальной оценке совокупности пар точек в каждом канале дальности, в которых происходит изменение параметра распределения отсчетов сначала в «направлении фон-цель», а затем в «направлении цель-фон».
Оптимальный по максимуму функции правдоподобия алгоритм нахождения оценок координат граничных точек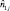 
и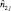 
j-м канале дальности принимает вид:
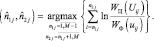(4.2.3)
Совокупность граничных точек n1j, n2j при каждом значении j образуют границу области Ω, занимаемой целью соответствующего класса.
Определим структуру оптимального алгоритма для некоторых наиболее распространенных видов распределений одномерной плотности вероятности отсчетов РЛИ.
а) Распределение отсчетов РЛИ – экспоненциальное:
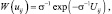(4.2.4)
причем его параметр σ пропорционален удельной ЭПР цели (σ2) или фона (σ1) в зависимости от того, расположен ли соответствующий отсчет в области цели ΩЦ или фона ΩФ. При известных априори значениях параметров σ1 и σ2 алгоритм (4.2.3) может быть записан в виде:
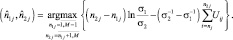(4.2.5)
При неизвестных значениях параметров σ1 и σ2 функция правдоподобия в каждом канале дальности может быть определена по формуле (4.2.5), где вместо названных параметров используются их максимально правдоподобные оценки при каждом возможном значении координат граничных точек n1 и n2. В этом случае алгоритм оценки координат граничных точек принимает вид:
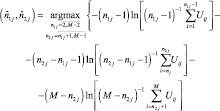(4.2.6)
и может быть назван адаптивным по отношению к параметрам распределения.
б) Распределение отсчетов РЛИ – гамма-распределение:
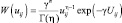
с параметрами γ2, η2 в области цели и параметрами γ1, η1 в области, занятой фоном.
Рассмотрим два варианта:
1) на границе областей изменяется только параметр масштаба γ (η2 = η1 = η). В этом случае алгоритм оценки граничных точек имеет вид:
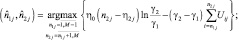(4.2.7)
2) на границе областей изменяется только параметр формы η (γ2 = γ1 = η0). Алгоритм выглядит следующим образом.
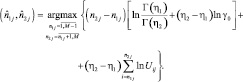(4.2.8)
Реализация рассмотренных алгоритмов не требует операций более сложных, нежели простое суммирование отсчетов РЛИ.