Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.6. Оценка радиолокационного портрета ПРЦ
Проблема создания банка данных РЛИ ПРЦ является основной при реализации алгоритма классификации, поскольку именно от количества и достоверности априорной информации зависит в конечном счёте эффективность решения задачи в целом.
В данном разделе рассматривается алгоритм многомерной оценки амплитуд отражённых сигналов и угловых координат их источников, реализующий многоканальную (по числу пеленгуемых источников) итеративную процедуру измерения по методу максимального правдоподобия и отличающийся сравнительно несложной технической реализацией [14].
Предположим, что наблюдение поля сигналов и помех производится эквидистантной антенной решеткой, длина которой L, а число приемных элементов М. Тот факт, что названная решётка создаётся в виде искусственного раскрыва, не оказывает влияния на решение задачи, так как в течение времени синтезирования параметры отражённых сигналов остаются практически неизменными, а это значит, что и принимаемые комплексные амплитуды остаются в пределах интервала синтезирования неизменными. Очевидно, что принимаемые комплексные амплитуды в каждой точке траектории должны запоминаться на всё время работы алгоритма. При N источниках сигналов, находящихся в дальней зоне приемной антенны и отличающихся своими комплексными амплитудами fi и угловыми направлениями Θi (i = 1, N), вектор комплексных амплитуд в элементах решетки может быть представлен в виде
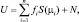(4.6.1)
где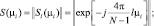 
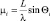(4.6.2)
– нормированная угловая координата i-го источника (λ – длина волны); N – вектор комплексных амплитуд помехи в элементах антенны.
Считая амплитуды отражённых сигналов и угловые координаты источников неслучайными неизвестными величинами, помеху гауссовой с нулевым математическим ожиданием и корреляционной матрицей Rш = M{NN*}, запишем функцию правдоподобия для неизвестных параметров сигналов fi и μi (i = 1, N):
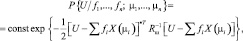(4.6.3)
где * – знак эрмитова сопряжения.
Преобразуем показатель (4.6.3) таким образом, чтобы выделить член, зависящий от амплитуды и угловой координаты только одного, например, m-го источника:
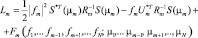(4.6.4)
где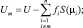 
(4.6.5)
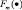– функция, не зависящая от fm и μm.
Для определения оценок максимального правдоподобия амплитуды и угловой координаты m-го отражающего элемента необходимо отыскать минимум выражения (4.6.4) по названным переменным. Преобразовав (4.6.4) к виду
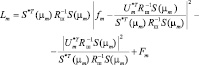(4.6.6)
замечаем что, максимум функции правдоподобия имеет при условии
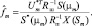(4.6.7)
Подставляя найденную оценку амплитуды (4.6.7.) в выражение (4.6.4) и дифференцируя по μm, получаем уравнение правдоподобия для оценки углового направления
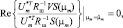(4.6.9)
где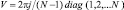 
– диагональная матрица.
Уравнение (4.6.8) легко решается численными методами, либо разложением в степенной ряд в окрестности оцениваемого значения.
Оценки параметров других сигналов находятся аналогично, причем перед оценкой m-го сигнала по формулам (4.6.7), (4.6.8) используются соответствующие оценки всех остальных n – 1 сигналов с целью компенсации «мешающих» для текущей оценки сигналов во входных данных m-го канала измерения.
Структурная схема оптимального алгоритма (рис. 4.10) состоит из n перекрестно связанных каналов, в каждом из которых производится вычитание оценок мешающих сигналов, полученных в соседних каналах, измерение «своих» параметров f и μ формирование оценки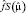 
«своего» сигнала, которая используется для соответствующей компенсации в других каналах.
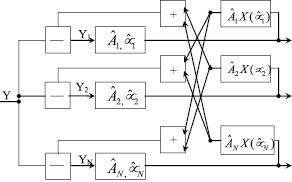
Рис. 4.10. Структурная схема измерений
Эффективность алгоритма исследовалась методом статистического моделирования на примере решения задачи измерения координат двух источников с угловыми направлениями μ1 = 0,2 и μ2 = –0,2, что соответствует их разнесению на 0,23 ширины диаграммы направленности антенной решетки по нулям (рис. 4.11). В качестве начальных условий задавались значения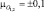 
(кривая 1), 
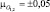(кривая 2), 
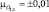(кривая 3). Шумы в элементах решетки некоррелированы. Отношение амплитуды сигнала к СКО шума 20 дБ. Оценки координат сходятся к истинным после 15…20 итераций при отличии заданных значений координат от начальных условий алгоритма в 10 и более раз.
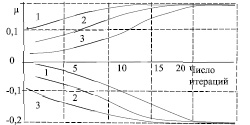
Рис. 4.11. Сходимость оценок координат источников
Таким образом, даже в тех случаях, когда сигналы не разрешаются по углу (в смысле релеевского критерия) при отношениях сигнал – шум, не существенно превышающих порог обнаружения, рассматриваемый алгоритм позволяет производить совместное измерение угловых координат при низких требованиях к точности установки начальных условий.