Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПРИЁМ И ОБРАБОТКА СИГНАЛОВ ОТ СЛОЖНЫХ ЦЕЛЕЙ

Доросинский Л. Г., Трухин М. П.,

5.3. Модель отраженного сигнала

На основе рассмотренных ранее моделей движения, состава и взаимного расположения элементов ПРЦ вводится математическая модель полного отраженного сигнала. Выбор статистических законов отражения определяется соотношениями между длиной волны и максимальными линейными размерами элементов.

В общем случае отраженный сигнал S(t) в точке приема равен сумме отраженных сигналов от отдельных элементов ПРЦ, а также сигналов, появляющихся в результате взаимных переотражений, многолучевого распространения и т. д.

Вследствие большого удаления элементов ПРЦ друг от друга (более 7–10 км [5]), а также сравнимости длины волны и линейных размеров элементов, эффекты, связанные с переотражениями, экранированием и т. п. играют исчезающе малую роль. Поэтому полагаем, что полный отраженный сигнал соответствует сумме сигналов, отраженных от каждого из элементов ПРЦ: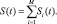

Определим парциальный отраженный сигнал S(t) в виде:

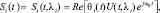(5.15)

где θi(t) – комплексный случайный коэффициент, зависящий от мощности зондирующего сигнала Pпер(t), коэффициента ослабления ξi(t) и фазового сдвига при отражении φi:

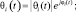
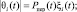
U(t, λi) – комплексный коэффициент детерминированной модуляции, выражающейся через амплитудную 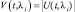и фазовую φ(t, λi) = arg (U(t, λi)) модуляции; λi – параметр сигнала, в общем случае векторный, например, временная задержка и доплеровский сдвиг λi = [τi, Ωi]Т.

Коэффициент ослабления определяется из уравнения радиолокации [9]:

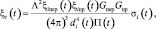(5.16)

где ξi пер(t) и ξi пр(t) – коэффициенты, учитывающие неидеальность распространения (рассеяния) электромагнитных волн при прямом и обратном распространении соответственно; GперGпр – коэффициенты усиления передающей и приемной антенн; Π(t) – потери, связанные с неидеальность приемного устройства; σi(t) – эффективная поверхность рассеяния (ЭПР) i-го элемента; Λ – длина волны.

На небольших интервалах времени наблюдения коэффициент ослабления можно представить в виде мультипликативного выражения

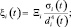(5.17)

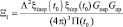, (5.18)

в котором t0 = (tнч + tкн)/2; tнч – начало; tкн – конец интервала наблюдения.

При постоянной мощности зондирующего сигнала случайные изменения θi(t) определяются флуктуациями ЭПР σi(t) и фазы отражения φi(t). Флуктуации ЭПР в зависимости от ориентации элемента относительно направления зондирования определяются, по данным [5], величиной ±20 дБ относительно  – средней ЭПР и приближенно описываются при Λ < bmax (bmax – максимальный линейный размер элемента) экспоненциальным законом распределения.

(5.19)

В модели (5.19) отсутствует «блестящая точка» в составе элемента. Для случая, когда, Λ ≈ bmax, более точной является модель с наличием «блестящей точки», в которой амплитуда A отраженного сигнала связана со среднеквадратичным отклонением диффузного отражения соотношением

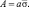(5.20)

Выбор параметра a этой модели (модель Райса [6, 10]) зависит от соотношения Λ и bmax, конструкции элемента, его покрытий и т. п.

Другими моделями, применяющимися при описании флуктуаций ЭПР, является предложенное Сверлингом [11] семейство хи-квадрат распределения:

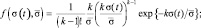σ(t) ≥ 0, (5.21)

которое было обобщено в [12] на случай не целых m = k и, тем самым, сведено к семейству гамма-распределения. В работе [13] подробно рассмотрен случай малых m (1 ≤ m ≤ 2), что объясняется заметными вероятностями больших значений ЭПР вытянутых цилиндрических тел. Поскольку параметр распределения (5.21) определяется по формуле

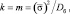(5.22)

то при больших дисперсиях Dб число степеней свободы достаточно мало. Отметим, что согласно (5.22), основой для выбора модели является ожидаемый разброс значений ЭПР относительно средней величины, поэтому стандартные модели достаточно правильно отображают характеристики рассеяния реальных целей в средней части функции распределения при условии приемлемого совпадения на «хвостах».

Спектр флуктуации σi(t) имеет эффективную ширину в единицы герц [14], поэтому при зондировании с большим периодом повторения (Τп > τк, τк – время корреляции ЭПР) из условия однозначности определения дальности до удаленных целей случайные ЭПР в соседних периодах независимы. Как уже указывалось в параграфе 5.2, ЭПР всех элементов ПРЦ по организационно-тактическим причинам выбираются одинаковыми.

Фаза отражения φi(t) – случайная величина, зависящая от ракурса, под которым наблюдается элемент, геометрических форм, свойств покрытия и т. д. Изменения φi(t) во времени определяют спектр фазовых флуктуаций шириной также в единицы герц. Распределение фаз диффузного отражения равномерно в интервале (0, 2π), кроме того при большом периоде повторения эти случайные фазы также независимы.

При сделанных выше предположениях о моделях распределения ЭПР и фаз отражения законы распределения модуля имеют вид:

1) для экспоненциального распределения –

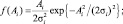Ai ≥ 0; (5.23)

– релеевское распределение. Здесь, и в формулах (5.24) и (5.25) параметр 2 – мощность диффузной составляющей;

2) для модели Райса –

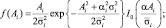Ai ≥ 0; (5.24)

3) для гамма-распределения –

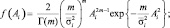Ai ≥ 0. (5.25)

Последнее распределение – это также распределение Накагами или m-распределение [6, 10]. На рис. 5.7 показана точка A, относящаяся к релеевскому распределению и кривая, характеризующая распределение Райса.

Рассмотрим изменение комплексного коэффициента модуляции, обусловленное отражением от движущегося по линейному закону элемента ПРЦ. Обоснование линейности движения было проведено в параграфе 5.2. Временная задержка до i-го элемента равна τi(t) = 2di(t)/c, доплеровская частота определяется постоянной радиальной скоростью 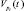и несущей частотой ω0: 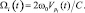Эти величины полностью описывают изменения постоянной составляющей комплексного коэффициента модуляции: сдвиг на τi(t) по времени и на Ωi(t) по частоте. При условии узкополостности зондирующего сигнала (Δφ  ω0T) пренебрегаем [14] дополнительными приращениями по времени и частоте других составляющих, считая, что весь спектр комплексной модуляции дружно сдвигается по времени на τi(t) и по частоте – на Ωi(t).

Взаимный сдвиг парциальных спектров определяется разностью радиальных скоростей отдельных элементов ПРЦ. Например, для приведенной выше траектории № 18 при скорости выброса 50 м/с и наклонной дальности 2000 км и РЛС, находящейся на расстоянии 500 км от точки падения, максимальная разность скоростей составляет ΔVpmax = 6,312 – 6,145 = 0,167 км/с. Следовательно, максимальный сдвиг спектров в этом случае равен от полного доплеровского сдвига. Взаимное расположение параметров λi коэффициентов комплексной модуляции (см. формулу (5.15)) на плоскости (τ, Ω), соответствующее ПРЦ на рис. 5.10, а, показано на рис. 5.11.

Парциальные временные задержки τi(t) могут быть представлены в виде τi(t) = τ0(t) + τi0(t), где τ0(t) – задержка до некоторой произвольно выбранной характерной точки ПРЦ (ближайший элемент, геометрический центр, энергетический центр и т. д.), τi0(t) – относительная временная задержка i-го элемента. Аналогичное выражение записывается для доплеровских частот: Ωi(t) = Ω0(t) + Ωi0(t).

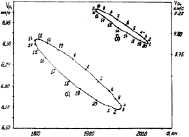
Рис. 5.10. Границы параметров элементов ПРЦ на (τ, Ω)-плоскости:
а – траектория № 18

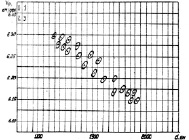
Рис. 5.11. Отклик согласованного фильтра при зондировании ПРЦ.
Траектория № 18, Vв = 50 м/с

Рассмотрим более подробно распределение последовательных во времени задержек в условиях приема сигналов на фоне шума. Предположим, что в момент начала зондирования параметры характерной точки имеют величину 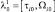, а ПРЦ на (τ, Ω)-плоскости занимает область Δτ×ΔΩ. Совместный закон изменения этих параметров в N периодах повторения аппроксимируется двумерной односвязной марковской последовательностью

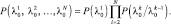(5.26)

Параметры марковского процесса (5.26) при линейной модели движения определяются следующим образом: коэффициент сноса для временных задержек равен

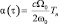, (5.27)

где Tn – период повторения, коэффициент сноса для доплеровских частот равен нулю, коэффициенты диффузии практически одинаковы и зависят от уровня шума.

Область предполагаемого расположения ПРЦ разбивается на одинаковые элементарные площадки δτ×δΩ. Общее число таких площадок 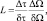каждой присвоен порядковый номер. Обозначим некоторое q-е сочетание элементов как вектор 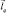(координатами вектора являются номера тех площадок, в которых присутствуют элементы ПРЦ) и запишем плотность вероятности расположения в k-м периоде

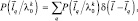(5.28)

где 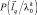 – вероятность q-го сочетания в k-м периоде. Сумма в (5.28) берется по всем возможным расположениям. Для фиксированного сочетания площадок в k-м периоде, содержащих элементы ПРЦ, зададим условную плотность вероятности вектора параметров 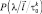. С учетом принятых предположений совместная плотность вероятности параметров парциальных отраженных сигналов в N периодах повторения имеет вид:

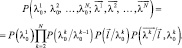(5.29)

В заключении рассмотрим вид радиолокационного отраженного сигнала на выходе согласованного фильтра. Отклик такого фильтра на один парциальный сигнал описывается функцией неопределенности зондирующего сигнала [9]

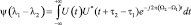
в виде ei(t) = ϑi(t)ψ(λ0 – λi), где опущены постоянные задержки. При λ0 = 0 отклик согласованного фильтра на полный отраженный сигнал равен

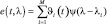. (5.30)

Пример представления e(t) на (τ, Ω)-плоскости при зондирующем колебании в виде гладкого прямоугольного радиоимпульса приведен на рис. 5.11. Здесь принято ϑi(t) = 1.

При близком расположении параметров λi происходит взаимное наложение спектров сигналов e(t, λi), приводящее к появлению зависимости сигнала, соответствующего некоторой элементарной площадке, от нескольких элементов ПРЦ. В табл. 5.5 приведены уровни коррелированности сигналов, соответствующих центрам соседних элементарных площадок (O-1 – по задержке, О-2 – по доплеровской частоте, О-3 – по задержке и доплеровской частоте (см. рис. 5.11), O-0 означает коэффициент автокорреляции) для четырех типов зондирующего колебания и пяти уровней плотности на плоскости.

Таблица 5.5

Уровни коррелированности сигналов на выходе согласованного фильтра

Тип сигнала

ρλ

O-0

O-1

O-2

O-3

без ЛЧМ

0,25

0,075

0,021

–0,037

–0,035

0,5

0,143

0,021

–0,038

–0,048

1

0,228

0,029

–0,036

–0,075

2

0,333

0,065

–0,067

–0,111

4

0,428

0,035

–0,066

–0,112

с ЛЧМ

0,25

0,070

0,014

–0,025

–0,025

0,5

0,149

0,017

–0,038

–0,038

1

0,202

0,022

–0,030

–0,038

2

0,274

0,017

–0,048

–0,034

4

0,308

0,039

–0, 045

–0,027

без ЛЧМ

0,25

0,099

0,009

–0,027

–0,051

0,5

0,186

0,007

–0,022

–0,086

1

0,308

0,016

–0,002

–0,120

2

0,426

0,064

–0,019

–0,150

4

0,545

0,034

–0,018

–0,155

с ЛЧМ

0,25

0,089

0,029

–0,022

–0,023

0,5

0,204

0,049

–0,043

–0,043

1

0,284

0,085

–0,041

–0,047

2

0,381

0,102

–0,058

–0,041

4

0,433

0,143

–0,062

–0,036

Размер элементарных площадок по оси задержек равен эффективной длительности импульсов τэф, по оси частот Ωэф [9]. Под плотностью параметра ρλ понимается среднее число точек, приходящихся на одну площадку.

Приведенные в табл. 5.5 уровни коррелированности позволяют указать соотношения между значениями плотности параметра ρλ и отношением сигнал/шум и оценить возможности использования исследуемых законов модуляции для формирования зондирующих колебаний. При обработке сигналов от многих целей гауссов закон модуляции имеет преимущества перед прямоугольным законом, особенно без ЛМЧ-заполнения. Однако наилучшим (нереализуемым) законом модуляции зондирующего колебания является такой закон, который обеспечивает формирование прямоугольной функции неопределенности:

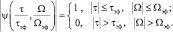(5.31)

В этом случае исключаются потери при дискретизации принимаемого колебания, возникающие за счет неопределенности местоположения элементов в объеме разрешения, а также взаимные помехи между отсчетами, обусловленные большими уровнями «хвостов» функции неопределённости 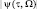. Вопросы синтеза реализуемых законов модуляции выходят за рамки настоящей работы, они рассмотрены, например, в работах [8, 15].