Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПРИЁМ И ОБРАБОТКА СИГНАЛОВ ОТ СЛОЖНЫХ ЦЕЛЕЙ

Доросинский Л. Г., Трухин М. П.,

7.1.1. Неодинаковые Pi

Проведем упрощение оптимального алгоритма (6.15) при отношении сигнал/шум, стремящемся к нулю (g → 0), и релеевской модели отраженных сигналов. В этом случае экспоненту с достаточной степенью точности можно представить двумя первыми членами ряда Тейлора в окрестности точки g = 0:

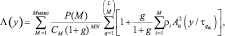(7.1)

где все обозначения те же, что были использованы в параграфе 5.1. Упростим это выражение, для чего исключим из него постоянное слагаемое, отнеся его в порог:

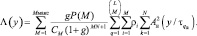(7.2)

Двойная сумма 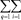содержит всего 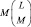слагаемых вида 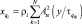и симметрична относительно каждого . Следовательно, имеется равенство:

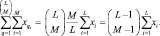(7.3)

Подставив правую часть (7.1) в (7.2), получим

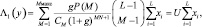(7.4)

где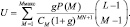

Итак, без учета постоянного множителя, который может быть отнесен в изменение порога, получившийся квазиоптимальный алгоритм (7.4) с весовым накоплением принятых сигналов за все время наблюдения асимптотически эквивалентен при g → 0 оптимальному алгоритму. Вес ρi, 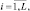определяется вероятностью Pi, 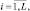появления отраженного сигнала в i-м объеме разрешения ρi = γPi, где γ – любая константа, например, L. При релеевской модели флуктуаций амплитуд отраженных сигналов этот алгоритм соответствует широко используемому квадратичному детектору с весовым линейным интегратором:

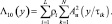(7.5)

При другой модели отраженных сигналов изменится лишь вид нелинейной операции – логарифма отношения правдоподобия – на входе весового интегратора:

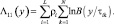(7.6)

Формирование статистики Λ10 можно выполнить на ЭЦВМ с числом разрядов регистров арифметического устройства, большим 20, причем, в случае существенно различающихся ρi форма представления числа должна быть плавающей. Число уровней квантования аналого-цифрового преобразователя (АЦП) должно соответствовать числу разрядов регистров. Необходимая машинная память 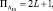машинное время –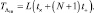

Определим зависимость вероятности правильного обнаружения D = D(L, T, g) и ложной тревоги T = T(L, T) от порога принятия решения T и радиолокационных параметров L и g. Для этого найдем вид распределения f(Λ) случайной величины Λ10 на выходе линейного интегратора после обработки сигналов за N периодов повторения. Поскольку статистика Λ10 есть взвешенная сумма случайных величин 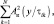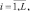имеющих хи-квадрат распределение с 2N степенями свободы [1], то при отыскании f(Λ) можно воспользоваться методом характеристических функций. Характеристическая функция распределения 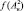имеет вид:

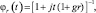ri ∈ {0, 1}. (7.7)

В выражении (7.7) r = 0 соответствует чисто шумовому отсчету, r = 1 – отсчету, являющемуся суммой отраженного сигнала и шума приемника. В этих обозначениях характеристическая функция распределения статистики 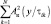равна

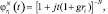ri ∈ {0, 1}, 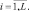(7.8)

Умножение на вес ρi несущественно изменяет вид характеристических функций:

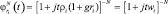, (7.9)

где wi = ρi(1 + gri),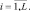

Предположим, что коэффициенты wi попарно не равны: wi ≠ wk, i ≠ k, 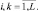Тогда характеристическая функция статистики Λ10 для одной из ситуаций при заданном числе элементов ПРЦ M соответствует произведению L характеристических функций (7.9):

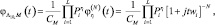(7.10)

где целые величины ri удовлетворяют условию 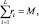ri ∈ {0, 1}.

Характеристическая функция статистики Λ10, усредненная по всем возможным ситуациям, имеет вид:

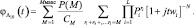(7.11)

Вероятность правильного обнаружения D находится интегрированием обратного преобразования Фурье от (7.11) в пределах от T до ∞:

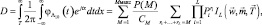(7.12)

где интеграл 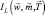вычислен в [2] в общей форме. Здесь вектор коэффициентов 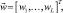вектор показателей степени 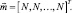Оба вектора имеют размерность L. Итак,

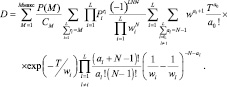(7.13)

Вероятность ложной тревоги F находится по выражению (7.13) при подстановке в него значений P(M) = d(M), M = 0, g = 0, где :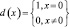

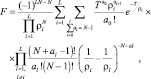(7.14)

В частности, при N = 1 формула (7.14) существенно упрощается:

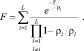(7.15)

Вычисление порога T согласно (7.15) реализовано в процедуре FIN, приведенной в [2].

Использование точных аналитических выражений (7.13) и (7.14) для расчета характеристик обнаружения наталкивается на большие вычислительные трудности даже при малых значениях L и Mмакс. Эти трудности обусловлены двумя причинами: ограниченным числом разрядов в представлении чисел на ЭЦВМ (обычно не более 12) и экспоненциально возрастающим количеством (~2L) анализируемых ситуаций. Первая причина приводит к таким большим ошибкам, вторая – к таким затратам машинного времени, что уже при L > 16 единственно возможным методом получения характеристик обнаружения на ЭЦВМ является метод статистического моделирования. Для снижения числа испытаний и повышения точности анализа значения порога T определяется по формуле (7.14). При разрешении (7.14) относительно T используется двойная точность (24 значащих цифры) и метод Ньютона [3].

Если некоторые из коэффициентов wi попарно равны, то вид выражения (7.13) для вероятности правильного обнаружения остается прежним, изменяются лишь параметры интеграла 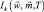. Например, при двух одинаковых ρi = ρj, i ≠ j, k = L – 1, mi = 2N, величины mj и wj из состава векторов и  исключаются.