Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.2.1. Неодинаковые Pi
Допустим, что каждый разряд на выходе АЦП соответствует целой степени 2. Общее число уровней квантования АЦП обозначим R, число разрядов B = [log2 R] + 1. Следовательно, минимальное число, отличное от нуля, равно единице, максимальное – 2B–1, динамический диапазон – 6,02(B – 1) Дб по напряжению. Введем вектор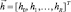 
уровней квантования. В общем случае h0 ≠ 0. Целочисленная квазиоптимальная статистика находится по следующему алгоритму, записываемому на основании аналогового алгоритма (7.5):
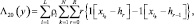(7.22)
где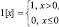 
– единичная функция; ρi – целые весовые коэффициенты, соответствующие вероятностям наличия отраженных сигналов в i-м элементе разрешения;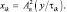 
При реализации алгоритма (7.22) необходимо провести L∙N квантований нормированной амплитуды xi и выполнить L(N + 1) умножений и L сложений R-значных чисел: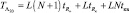 
. Требуемая машинная память составляет 
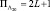ячеек, предназначенных для хранения R-значных чисел.
Характеристики обнаружения алгоритма (7.22) находятся методом производящих функций. Определим вид производящей функции статистики Λ20 в одном периоде повторения. Отсчёт на выходе АЦП в некотором интервале разрешения может соответствовать либо шуму, либо шуму + сигналу. Вероятность появления отсчёта, равного r,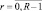 
, в первом случае обозначим μ0(r), во втором случае – μ1(r).
Эти вероятности определяются соотношениями
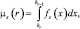s ∈ {0,1}; hR+1 = ∞, (7.23)
где fs(x), s ∈ {0, 1} – плотности распределения случайной величины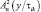 
на входе АЦП при отсутствии и наличии отраженного сигнала. При релеевской модели отраженных сигналов и условии, что они разрешены, эти величины равны
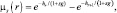s ∈ {0, 1}. (7.24)
Производящая функция ψs целочисленной величины y на выходе АЦП строится на основании вероятностей μs(r) [7]:
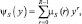s ∈ {0, 1}. (7.25)
Очевидно, при умноженииy на целый весовой коэффициент ρ производящая функция новой величины z = ρy полностью определяется выражением (7.25):
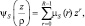s ∈ {0, 1}. (7.26)
Это выражение можно записать относительно всех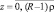 
, если доопределить μs(r) при нецелых r равными нулю:
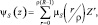s ∈ {0, 1}. (7.27)
Тогда производящая функция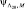 
при наличии M отраженных сигналов имеет вид:
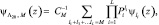li = {0, 1}, (7.28)
где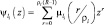 
.
Производящая функция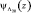 
статистики Λ20 за все время наблюдения, усредненная по случайному числу элементов ПРЦ, легко находится по формуле (7.28):
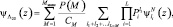li = {0, 1}. (7.29)
Переходя от производящей функции (7.29) к распределению вероятности P(Λ20) и суммируя его в пределах от целочисленного порога T до LN(R – 1), получим вероятность правильного обнаружения алгоритмом (7.22) дружно движущейся ПРЦ с разрешаемыми элементами:
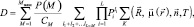(7.30)
где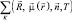 
– вычисленная в [2] сумма от обратного Z-преобразования производящей функции 
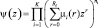в пределах от T до 
.
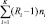В формуле (7.30) K = L; Ri = (R – 1)ρi;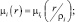 
ni = N,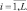 
Таким образом, вероятность правильного обнаружения D определяется по формуле
(7.31)
где оба последних произведения выполняются по всем совместным решениям в целых числах двух подстрочных уравнений.
Вероятность ложной тревоги находится с помощью подстановки в (7.31) условий M = 0, P(M) = d(M), g = 0:
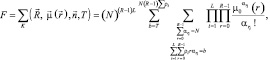(7.31)
где μ0(r) находится из (7.24) при s = 0;
Ri = (R – 1)ρi;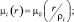 
ni = N,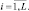 
Практически расчет характеристик обнаружения по формулам (7.31) и (7.32) возможен при LNR < 30–40. Если произведение LNR превышает эту границу, то необходимо обратиться к приближенным методам – статистическому моделированию или разложению распределений в ряды Эджворта [1] и Грама-Шарлье [8]. В последнем случае затраты машинного времени уменьшаются несущественно, так как вместо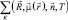 
в (7.30) требуется вычислить сумму семиинвариантов для L производящих функций. Эти семиинварианты находятся по формулам, приведенным в [9, 10]. Вычисления проводятся в начале работы программы, количество ячеек на хранение j семиинвариантов каждой производящей функции равно 2jL. Переход от семиинвариантов к вероятностям и наоборот может быть выполнен с помощью процедуры FRSH [2].
Приведем выражения характеристик обнаружения для важного частного случая, когда число уровней квантования равно двум (R = 2).
Этот случай соответствует наиболее простому – бинарному – квантованию принимаемого сигнала. Вероятность правильного обнаружения согласно (7.31) при R = 2 равна:
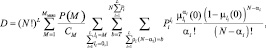(7.32)
где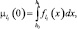 
li ∈ {0,1}; li = 0 соответствует шуму, li = 1 – шуму + сигналу; f0(x), f1(x) – соответствующие плотности распределений случайного процесса на входе АЦП. В частности, если N = 1, то
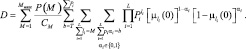(7.33)
Вероятность ложной тревоги находится подстановкой в (7.33) M = 0, g = 0, P(M) = d(M):
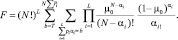(7.34)
При N = 1 она равна
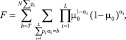
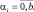(7.35)
Количество слагаемых в формуле (7.35), определяемое выражением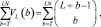 
резко возрастает с увеличением LN (скорость роста превышает экспоненциальную). При N = 1 количество слагаемых, равное 
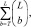увеличивается не быстрее, чем 2L–1. Эти оценки скорости роста справедливы при больших вероятностях ложных тревог (F > 0,1) При F 0,1 и R ≤ 8 количество слагаемых в обоих уравнениях с увеличением L и N возрастает почти по линейному закону.