Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПРИЁМ И ОБРАБОТКА СИГНАЛОВ ОТ СЛОЖНЫХ ЦЕЛЕЙ

Доросинский Л. Г., Трухин М. П.,

7.2.2. Одинаковые Pi

В этом случае целочисленная статистика обнаружения находится по алгоритму простого (невзвешенного) суммирования:

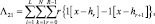(7.36)

где все обозначения аналогичны обозначениям, применявшимся при записи алгоритма Λ20 в пункте 7.2.1. Очевидно, что характеристики обнаружения алгоритма (7.37) могут быть найдены по формулам предыдущего пункта при условии, что все Pi одинаковы и равны 1/L: 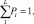Машинное время и память при формировании статистики Λ21 меньше, чем в предыдущем случае: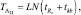 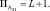Вероятность правильного обнаружения равна

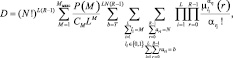(7.37)

где величины 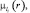li ∈ {0, 1} рассчитываются по формуле (7.24).

Вероятность ложной тревоги находится по формуле (7.38) при условии, что P(M) = d(M); M = 0, g = 0:

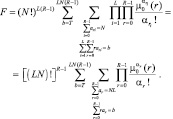(7.38)

В [2] приведены процедуры DSC4IN и DSC8IN, используя которые можно найти величину порога T соответственно при R = 4 и R = 8 для заданной вероятности F.

Приведем также формулы для расчета характеристик обнаружения в важном случае бинарного квантования (R = 2) принятого сигнала:

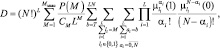(7.39)

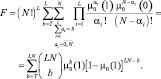(7.40)

При выводе (7.41) использовано равенство 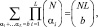доказанное в [11]. В [2] приведена процедура CIN, с помощью которой в зависимости от F и μ0(1) определяется целочисленный порог T или вероятность μ0(1) в зависимости F и T. Для приближенного вычисления вероятности ложной тревоги можно воспользоваться пуассоновским приближением биномиального распределения на его правом «хвосте», т. е.

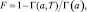(7.41)

где a = m0μ0(1).

Более сложным является определение F методом «перекошенных распределений вероятностей» [12] (модифицированных границ Чернова [13]), для которого необходимо знать кумулятивную функцию. Поскольку семиинварианты биномиального распределения имеют вид

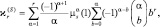s ∈ {0, 1}, 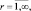(7.42)

то семиинварианты статистики Λ21 при отсутствии отраженных сигналов равны 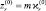. Кумулятивная функция биномиального распределения записывается в виде ряда

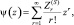s ∈ {0, 1}. (7.43)

Полное исследование квазиоптимального алгоритма с бинарным квантователем и линейным сумматором проведено в [10]. Вероятность правильного обнаружения определялась согласно формуле, которая является эквивалентной записью (7.40):

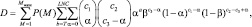(7.44)

где при m2 > b

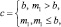c1 = m1, c2 = m2, c3 = b; α = μ1(1); β = μ0(1);

при m2 ≤ b, m1 < b

c = m – b, c1 = m2, c2 = m1, c3 = m – b; α = 1 – μ1(1), β = 1 – μ0(1);

при m2 ≤ b, m1 > b

c = c1 = m2, c2 = m1, c3 = b; α = μ1(1), β = μ0(1).

Здесь m = NL, m1 = (L – M)N, m2 = MN. Метод «перекошенных вероятностей» может быть использован и для приближенного вычисления вероятностей правильного обнаружения при условии, что в (7.44) семиинварианты 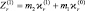. Более простой путь состоит в использовании 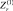при обращении к рядам Эджворта и Грама-Шарлье.

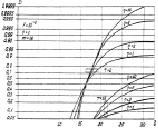
Характеристики обнаружения алгоритма (7.37) при R = 2, вычисленные по точным формулам при тех же значениях параметров обнаружения, что и алгоритма (7.16), и различных порогах T приведены на рис. 7.7–7.8.

а б

Рис. 7.7. Характеристики обнаружения алгоритма (7.37) при фиксированном втором параметре априорного распределения:
а – m = 8, б – m = 16

Рис. 7.8. Характеристики обнаружения алгоритма (7.37) при различных квазигауссовых априорных распределениях

Графики показывают, что алгоритм с бинарным квантователем в целом существенно хуже обнаруживает ПРЦ, чем алгоритм (7.16). На графиках наблюдается резкая зависимость от величины порога T, при уменьшении которого вероятность правильного обнаружения падает, а её зависимость от параметра ν возрастает. Особенно наглядно последняя связь проявляется при сравнении рис. 7.9, а и 7.10.

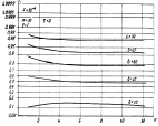
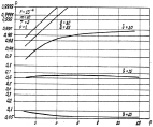
а б

Рис. 7.9. Влияние изменения второго (а) и первого (б) параметров априорного распределения на вероятности правильного обнаружения

Зависимость вероятности правильного обнаружения от параметра η при малых и средних слабая (рис. 7.9, б), при больших возрастание η приводит (как и при обнаружении ПРЦ алгоритмом (7.16)) к резкому увеличению вероятности правильного обнаружения. Влияние изменения параметра η в зависимости от m при различных отношениях сигнал/шум и ν = 1 показано на рис. 7.11. При малых характеристики для η = 1 и η = 10 близки во всем диапазоне изменений m, при средних и больших значениях появляется существенная зависимость D от значений η и m.

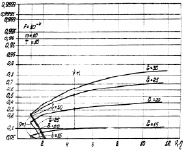
Рис. 7.10. Влияние изменения первого и второго параметров априорного распределения на вероятности правильного обнаружения

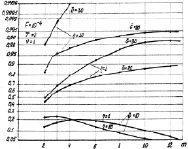
Рис. 7.11. Зависимости вероятности правильного обнаружения от числа объемов разрешения

Все графики на рис. 7.7–7.8 имеют характерную форму, становясь при больших практически горизонтальными. Действительно, алгоритм (7.37) имеет характеристики обнаружения, не стремящиеся при 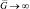к единице. Покажем это.

При 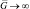(g → ∞) значение μ1(1) → 1. Подставив μ1(1) = 1 в (7.45), получим вероятность правильного обнаружения при бесконечно большой мощности отраженного сигнала:

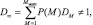T > 1, (7.45)

где 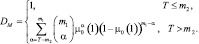(7.46)

Равенство D∞ = 1 выполняется лишь при T = 1, возможное при μ1(1) ≤ 1 – (1 – F)1/m. Заметим, что этот вывод справедлив при любых распределениях амплитуд сигнальных отсчетов. Зависимости D∞ от параметров априорного распределения показаны на рис. 7.12 и 7.13. Увеличение параметра η приводит к возрастанию, а увеличение параметра ν – к уменьшению D∞. Характер зависимости D∞ от порога T ясен из (7.47). На рис. 7.14 приведены зависимости D∞ от порога квантования, т. е. от μ0(1). Слева кривые стремятся к единице, а справа – к асимптотам, определяемым выражением (7.46) при условии, что 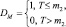Левое граничное значение μ0 = 1 определяется из заданного порога квантования и вероятности ложной тревоги и равно F 1/m, поэтому максимальное при данных параметрах значение обнаружения D∞ определяется согласно (7.46) при подстановке в (7.47) μ0(1) = μ0(1)max = F1/m.

а б

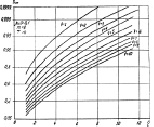
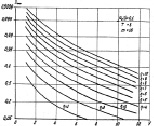
Рис. 7.12. Максимальные вероятности правильного обнаружения алгоритма (7.37):
а – m = 8, T = 4; б – m = 16, T = 8

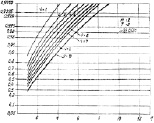
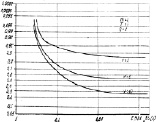
Рис. 7.13. Максимальные вероятности правильного обнаружения D∞
алгоритма (7.37)

Рис. 7.14. Максимальные вероятности правильного обнаружения алгоритма (7.37)
при различных порогах квантования

Исследуем зависимости вероятности правильного обнаружения D(T) от порога T, показанные на рис. 7.15 и рис. 7.16. Все графики показывают, в основном, уменьшение D при увеличении T. Лишь при малых и средних отношениях сигнал/шум имеется такое значение T0, при котором D – наибольшая для данной ситуации обнаружения. Следовательно, наилучшим целочисленным порогом принятия решения при больших является единица и двухэтапный обнаружитель превращается в одноэтапный, принимающий решение о наличии ПРЦ на основании сравнения с порогом только одного, самого большого значения из принятых, и, таким образом, алгоритм (7.37) сводится к алгоритму (7.55). Увеличение параметра η приводит к увеличению наилучшего порога T0 при всех 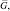действие ν на выбор T противоположно.

Рис. 7.15. Зависимости вероятностей правильного обнаружения алгоритма (7.37)
от порога принятия решения

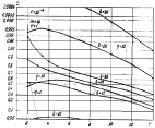
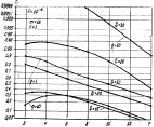
Рис. 7.16. Зависимости вероятности правильного обнаружения алгоритма (3.37)
от порога принятия решения

Представленные на рис. 7.17 и 7.18 графики являются усредненными вероятностями правильного обнаружения , как это показано на рис. 7.17, б. Цифры у изломов означают порог T, который может изменяться только дискретно. Увеличение порога квантования h1 (уменьшение μ0(1)) приводит к плавному изменению всех членов суммы в (7.42), а соответствующее изменению μ0(1) дискретное уменьшение порога T – к появлению новых членов в этой сумме, т. е. разрыву зависимости D(μ0(1)). Уменьшение μ0(1) при больших приводит к увеличению вероятности правильного обнаружения. При μ0(1) < 1 – (1 – F)1/m она начинает падать, что говорит о наличии глобального максимума кривых D(μ0(1)).

аб

Рис. 7.17. Усредненные вероятности правильного обнаружения в зависимости
от вероятности квантования шума:
а – равномерное распределение; б – многоэлементные ПРЦ

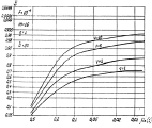
При малых имеется локальный максимум вблизи μ0(1) = 0,2, что совпадает с известным результатам [14]. Графики на рис. 7.18 показывают различный характер зависимостей вероятности D от параметров априорного распределения числа целей.

а б

Рис. 7.18. Усредненные вероятности правильного обнаружения
в зависимости от вероятности квантования шума:
а – малоэлементные ПРЦ; б – ПРЦ с квазигауссовым распределением

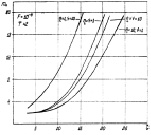
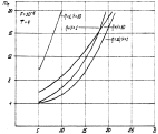
На рис 7.19 представлены графики зависимостей m0 от отношения сигнал/шум. Сравнение их с аналогичными графиками алгоритма (7.16) приводит к выводу, что в данном случае m0 значительно больше, чем у алгоритма (7.16). Наблюдается также сильная зависимость оптимального числа объёмов разрешения от вероятности ложной тревоги.

а б

Рис. 7.19. Оптимальное число объемов разрешения в области наблюдения алгоритма (7.37):
а – F = 10–4; б – F = 10–6

Численные характеристики обнаружения алгоритма с дискретным накоплением при числе уровней квантования R = 4,8,16 получены методом статистического моделирования. Число испытаний Q равнялось 1000, для D = 0,999 доверительный интервал при уровне значимости 95 % равен 0,002. В действительности он будет несколько меньше (0,0015), так как при таких значениях D более справедлива пуассонова аппроксимация биномиального распределения [60]. Реальные отклонения, как правило, значительно меньше (в 2–4 раза).

Таким образом, точность статистического моделирования при 1000 испытаний удовлетворительна и сравнима с точностью графического изображения характеристик обнаружения. Этот вывод относится ко всем моделируемым квазиоптимальным алгоритмам обнаружения для вероятностей в диапазоне 0,05 ≤ Dэкс ≤ 0,995 [2].

На рис. 7.20 изображены характеристики обнаружения для случаев многоэлементной и малоэлементной ПРЦ. Анализ характеристик показывает, что во втором случае наилучшим является бинарный квантователь. При D ≥ 0,9 выигрыш в пороговом сигнале по сравнению с другими малоуровневыми сумматорами (R = 4, 8, 16) может достигать больших значений (15 дБ), причем с ростом g этот выигрыш возрастает. Потери по сравнению с аналоговым на уровне D = 0,9 составляют 2,5 Дб. При иных типах распределений ПРЦ алгоритм (7.37) имеет лучшие характеристики для R > 2. Например, выигрыш в пороговом сигнале на уровне D = 0,9 и R = 16 равен 2,2 дБ и с ростом g уменьшается. Увеличение числа уровней квантования с двух до четырех приводит к резкому изменению характеристик обнаружения, при дальнейшем увеличении R это изменение менее заметно. При обнаружении многоэлементных целей кривые для R = 16 практически совпадают с таковыми алгоритма с аналоговым накоплением (7.16).

Рис. 7.20. Характеристики обнаружения алгоритма (7.37)
при различном числе уровней квантования

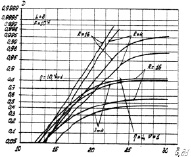
Рис. 7.21. Характеристики обнаружения алгоритма (7.37)
при двух типах формирования порогов квантования

Итак, бинарное квантование является наилучшим при обнаружении малоэлементной ПРЦ. Для обнаружения ПРЦ с иными видами априорных распределений следует использовать квантование на большее число уровней. Максимальное число уровней квантования равно 16. Дальнейшее увеличение не приводит к заметному улучшению качества обнаружения. С учетом затрат на реализацию наиболее приемлемым следует считать 4–8 уровней.

Одной из задач анализа алгоритма (7.37) являлось изучение влияния уровней (порогов) квантования hr, 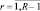на характеристики обнаружения. В качестве примера на рис. 7.21 приведены зависимости D для двух типов формирования порогов: первом, при котором hR–1 = 4,61 и равностоящих порогах, и втором, при котором вероятности μ0(r), 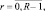одинаковы и равны 1/R. Выигрыш за счет применения первого типа порогов очень большой – от 5 дБ до 20 дБ. Хотя с ростом числа уровней квантования этот выигрыш уменьшается, однако во всех рассмотренных ситуациях он остается существенным. Результаты анализа показали, что чем больше число уровней квантования, тем более одинаковыми должны быть расстояния между порогами.

При этом верхний порог квантования hR–1 должен быть не меньше величины m = –lnF. Чем больше второй параметр априорного распределения, тем больше должен быть порог hR–1. В частности, для обнаружения малоэлементной цели следует принять hr–1 = (2–3)m. При бинарном квантовании порог определяется на основании приведенных выше в настоящем пункте результатов. Промежуточные случаи требуют более детального исследования с использованием оптимизационных методов, например, метода нелинейного программирования.