Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.3.1. Квазиоптимальный алгоритм с полным выбором максимума
При малом числе элементов ПРЦ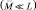 
и увеличении отношения сигнал/шум в оптимальной статистике (2.15) основную роль будет играть максимальный из всех принятых отсчетов. Особенно это проявляется, когда ПРЦ состоит из одного элемента.
В качестве иллюстрации исследуем соотношения между квазиоптимальным алгоритмом выбора максимума и оптимальным алгоритмом для простого случая, при котором число элементов ПРЦ равно единице, а число интервалов разрешения, приходящихся на ПРЦ равно 2, то есть L = 2, M = 1. Как шум, так и сигнал + шум имеют релеевское распределение амплитуд: на выходе квадратичного детектора дискретные отсчеты
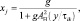
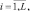
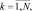
распределены по экспоненциальному закону. Оптимальная статистика Λ0 находится в соответствии с алгоритмом
Λ0 = exp(x1) + exp(x2), (7.48)
квазиоптимальная статистика
Λко = max(x1, x2). (7.49)
Вывод формулы для вероятности ложной тревоги алгоритма (7.48) приведен в [2] для целых величин k = 1 + (1 + g)/g:
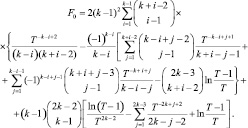(7.50)
Вероятность правильного обнаружения в этой простой ситуации выражается ещё более сложной зависимостью. Вероятность ложной тревоги Fk и правильного обнаружения Dk алгоритма (7.49) определяются простыми соотношениями:
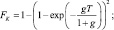
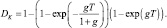(7.51)
Проведено сравнение для интересующего нас случая большого отношения сигнал/шум (g → ∞). Выбор максимума в этом случае будет представлять собой практически оптимальный алгоритм. Сопоставление характеристик обнаружения приводит к выводу, что оба алгоритма эквивалентны при g > 15 дБ и F < 0,1, при g < 15 дБ алгоритм (7.48) имеет несущественное превышение, отчетливо проявляющееся только при F > 0,1.
Неодинаковые Pi. В этом случае при указанных в начале параграфа условиях и релеевской модели отраженного сигнала оптимальный алгоритм (6.15) сводится к полному выбору максимума взвешенных отсчетов:
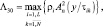(7.52)
где ρi – вес соответствующий вероятности Pi.
Это алгоритм эквивалентен алгоритму, состоящему в принятии решения о наличии цели при превышении порога хотя бы одним из значений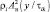 
. Операция сравнения с порогом сравнительно просто реализуется на ЭЦВМ, время ее выполнения в среднем на порядок меньше, чем любой арифметической операции. Например, время на реализацию
алгоритма (7.52) равно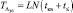 
, а для хранения информации необходима память L + 1 ячеек. Второе достоинство этого алгоритма состоит в том, что помимо факта обнаружения, с его помощью можно грубо оценить координаты обнаруживаемого объекта. Недостатком является неполный учет априорной информации о характере движения ПРЦ, поэтому он несколько уступает квазиоптимальному алгоритму с накоплением и выбором максимума, обсуждаемому ниже.
Характеристики обнаружения алгоритма (7.52) определяются с использованием обычных методов теории вероятностей [7]. Вероятность правильного обнаружения равна:
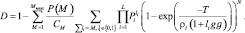(7.53)
Вероятность ложной тревоги находится из (7.53) при P(M) = d(M), M = 0, g = 0:
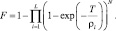(7.474)
Простой вид полученных аналитических выражений позволяет использовать их для расчета характеристик обнаружения при бόльших значениях L и Mмакс, чем в предыдущих параграфах (L < 50, Mмакс < L/4).
Одинаковые Pi. Весовые коэффициенты становятся одинаковыми, поэтому алгоритм (7.52) упрощается:
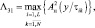(7.55)
Этот алгоритм обладает исключительной простотой. Время на его реализацию минимально: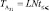 
, необходимая память также минимальна – 
Характеристика обнаружения легко приводится к свернутому виду
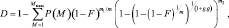(7.56)
где, как и ранее,
m = NL; m1 = N(L – M); m2 = NM.
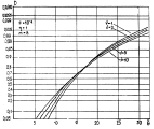
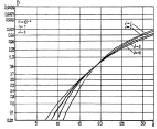
Здесь можно не обращаться к методу статистического моделирования при больших значениях m, если имеется возможность представления чисел на ЭЦВМ с двойной точностью. Графики характеристик обнаружения алгоритма (7.55) представлены на рис. 7.22–7.24.
а б
Рис. 7.22. Характеристики обнаружения алгоритма (7.55) при фиксированном первом параметре априорного распределения:
а – F = 10–4; б – F = 10–6
а б
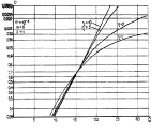
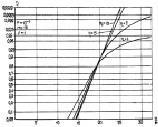
Рис. 7.23. Характеристики обнаружения алгоритма (7.55)
при фиксированном втором параметре:
а – m = 8; б – m = 16
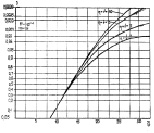
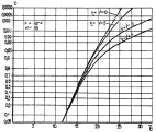
Сравнение графиков обоих алгоритмов приводит к выводу, что при малых и средних отношениях сигнал/шум алгоритм (7.55) проигрывает по качеству обнаружения алгоритму (7.16). Анализ зависимостей показывает, что чем больше отношение η2/(η + ν), тем ближе характеристики обнаружения к прямой линии, которая на используемой системе координат означает характеристику обнаружения детерминированного сигнала в нормальных шумах, т. е. интеграл вероятности в зависимости от его аргумента.
а б
Рис. 7.24. Характеристики обнаружения алгоритма (7.55)
при различных квазигауссовых априорных распределениях:
а – m = 8; б – m = 16
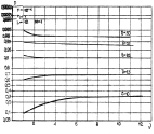
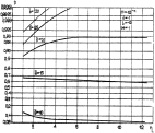
На рис. 7.25 показаны зависимости вероятности правильного обнаружения от параметров априорного распределения. Отличительной особенностью по сравнению с алгоритмом (5.16) при больших 
является сильная зависимость от первого параметра. Как и ранее, имеется такое значение 
(в данном случае ~15 дБ), при котором вероятность правильного обнаружения D алгоритма (7.55) не зависит от параметров априорного распределения.
а б
Рис. 7.25. Влияние изменения второго (а) и первого (б) параметров априорного распределения на вероятности правильного обнаружения (7.55)
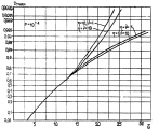
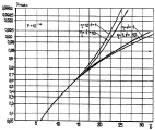
Графики на рис. 7.26 представляют зависимости максимально достижимых вероятностей правильного обнаружения Dmax при различных уровнях ложной тревоги. При малых и средних 
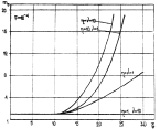
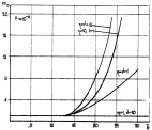
величины Dmax практически совпадают, при больших – различаются, особенно для η2/(η + ν) > 3. Зависимости оптимального числа интервалов разрешения m0 от отношения сигнал/шум 
показаны на рис. 7.27.
а б
Рис. 7.26. Максимально достижимые вероятности
правильного обнаружения алгоритма (7.55):
а – F = 10–4; б – F = 10–6
а б
Рис. 7.27. Оптимальное число объемов разрешения алгоритма (7.55):
а – F = 10–4; б – F = 10–6
Общий вывод из анализа графиков такой же, какой был сделан ранее для алгоритма (7.16): m0 = 1 при малых 
и m0 ≤ 20 при средних 
. Как и ожидалось, в среднем число m0 у алгоритма (7.55) меньше, чем у алгоритма (7.16).