Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.3.2. Квазиоптимальный алгоритм с межпериодным накоплением и выбором максимума
Как указывалось, рассмотренный в предыдущем пункте квазиоптимальный алгоритм с полным выбором максимума при формировании статистики не использует априорную информацию о характере движения ПРЦ. Если отказаться от выполненного выше крайнего упрощения оптимального алгоритма (6.15), то при тех же условиях (M мало, g → ∞) для обнаружения дружно движущейся ПРЦ следует использовать квазиоптимальный алгоритм с межпериодным накоплением и выбором максимума среди L накопленных отсчетов:
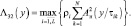(7.57)
Время на вычисление статистики Λ32 больше, чем в предыдущем случае: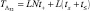 
, для хранения информации необходим бόльший объем памяти 
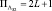ячеек.
Неодинаковые Pi. Вероятность обнаружения рассчитывается по формуле
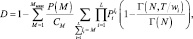(7.58)
где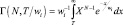 
– неполная гамма-функция,
wi = ρi(1 + li gɡ), li ∈ {0,1}.
Вероятность ложной тревоги находится согласно выражения
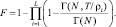(7.59)
Использование этих аналитических выражений для определения характеристик обнаружения не встречает больших трудностей. Вычисление Γ(N, X) следует проводить с помощью процедуры NG, описанной в [2].
Одинаковые Pi. При одинаковых вероятностях Pi алгоритм (7.57) имеет вид (он исследован в [16]):
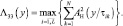(7.60)
Машинное время и машинная память здесь меньше примерно в два раза, чем в предыдущем подпункте:
.
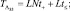
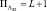Вероятность правильного обнаружения определяется по формуле
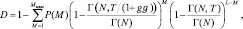(7.61)
Вероятность ложной тревоги –
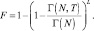(7.62)
При заданной величине F необходимый порог легко может быть найден с помощью процедуры ΓIN, первый аргумент которой равен N, второй – 1 – (1 – F)1/L. Процедура ΓIN(GIN) описана в [2]. Вычисление согласно выражению (7.61) проводится также относительно просто и быстро.
На рис. 7.28–7.30 представлены характеристики обнаружения алгоритма (7.60). На всех графиках видна одна и та же закономерность: при отношении сигнал/шум порядка 12–20 дБ вероятность правильного обнаружения при увеличении N уменьшается и довольно значительно, при больших G – возрастает. Чем больше отношение η2/(η + ν), тем круче и прямолинейнее кривые, тем меньше выигрыш за счет увеличения N при одинаковой общей энергии отраженных сигналов.
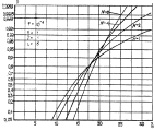
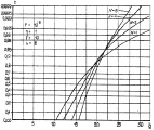
а б
Рис. 7.28. Характеристики обнаружения алгоритма (7.60) при равномерном (а) и малоэлементном (б) априорных распределениях
Например, на уровне D = 0,995 при F = 10–4,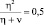 
энергетический выигрыш 
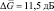, при 
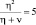он существенно меньше – 
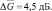Чем выше вероятность правильного обнаружения, тем больше значение 
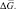Увеличение N более 8 для D < 0,9999 практически нецелесообразно, поскольку даже при 
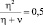в этом случае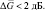 
а б
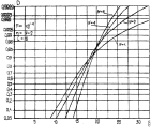
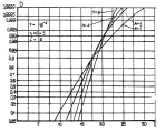
Рис. 7.29. Характеристики обнаружения алгоритма (7.60)
при квазигауссовых априорных распределениях:
а – η = ν = 2; б – η = ν = 5
а б
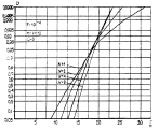
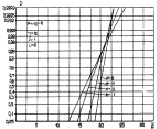
Рис. 7.30. Характеристики обнаружения алгоритма (7.60)
при квазигауссовом(а) и многоэлементном (б) априорных распределениях
На рис. 7.31 показаны зависимости вероятности правильного обнаружения от первого и второго параметров априорного распределения при N = 8. Анализ графиков показывает, что при любых отношениях сигнал/шум бόльшему значению ν соответствует бόльшая величина D. Характер влияния параметра η зависит от уровня 
: при большой величине возрастание η приводит к существенному увеличению D, при средних и, особенно, при малых 
– к уменьшению D.
а б
Рис. 7.31. Влияние изменения второго (а) и первого (б) параметров априорного распределения на вероятности правильного обнаружения алгоритма (7.60)
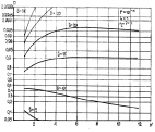
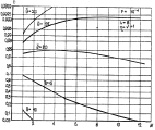
Влияние числа периодов повторения N на вероятность правильного обнаружения показано на рис. 7.32 и 7.33. Из графиков следует, что имеется оптимальное значение N0, при малых 
равное единице, при котором вероятность правильного обнаружения наибольшая. С уменьшением числа интервалов разрешения или увеличением отношения сигнал/шум значение N0 возрастает. При малых и средних 
N0 = 1 для L ≥ 4; чем больше L, тем выше значение 
, при котором N0 отличается от единицы. Априорное распределение также оказывает влияние на N0: чем меньше η/(η + ν), тем больше N0.
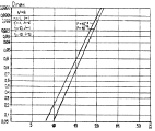
Зависимости максимальных вероятностей правильного обнаружения представлены на рис. 7.34. Это практически прямые линии, различие между ними за счет априорных распределений с увеличением N уменьшается и при N > 8 его практически нет. Это объясняется тем, что Dmax при N ≥ 8 соответствует оптимальному числу элементов разрешения, равному единице, поэтому все априорные распределения вырождаются в P(M) = d(M – 1).
а б
Рис. 7.32. Зависимости вероятностей правильного обнаружения алгоритма (7.60)
от числа периодов повторения при равномерном распределении:
а – L = 1; б – L = 8
а б
Рис. 7.33. Зависимости вероятностей правильного обнаружения алгоритма (7.60)
от числа периодов повторения:
а – L = 4; б – L = 8
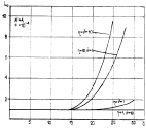
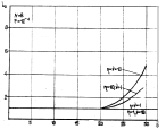
Графики на рис. 7.35 показывают, как зависит L0 от величины 
. Хорошо видна тенденция уменьшения L0 с увеличением N. При N > 10 в рассматриваемом диапазоне изменения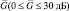 
можно принять L = 1 для всех случаев априорного распределения.
а б
Рис. 7.34. Максимально достижимые вероятности
правильного обнаружения алгоритма (7.60):
а – N = 4; б – N = 8
а б
Рис. 7.35. Оптимальное число объемов разрешения алгоритма (7.60)
в зависимости от отношения сигнал/шум:
а – N = 4; б – N = 8