Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.4. Квазиоптимальные алгоритмы с использованием порядковых статистик
В параграфе исследуются квазиоптимальные алгоритмы обнаружения ПРЦ, асимптотически оптимальные как при больших, так и при малых отношениях сигнал/шум и произвольном распределении числа элементов ПРЦ.
Предположим, что в формуле (6.15) N = 1 и значения реализаций xi = lnBi ранжированы и образуют вариационный ряд вида x(1) ≥ x (2) ≥ … ≥ x (L). При увеличении отношения сигнал/шум g первыми членами во все возрастающем количестве актов будут становиться отсчёты, относящиеся к отраженным сигналам от обнаруживаемых элементов. При достаточно большой величине ɡg среди первых M членов ряда практически будут отсутствовать шумовые отсчеты. На основании этого свойства вариационного ряда можно существенно упростить двойную сумму в (6.15) Поскольку среди всех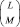 
сумма любых M членов ряда сумма его первых M членов наибольшая и с увеличением g все более отличается от остальных 
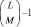сумм, то упрощенный алгоритм (N = 1) примет вид:
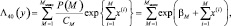(7.63)
где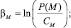 
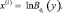
Практическая реализация этого алгоритма на неспециализированных ЭЦВМ невозможна вследствие выходящих за допустимые границы значений показателя экспоненты. Можно избавиться от этого недостатка, если формировать статистику согласно другому, более простому алгоритму
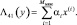(7.48)
Однако в этом случае число разрядов арифметического устройства должно быть не менее 15–20. Коэффициент αi сложным образом зависят от коэффициентов βM в формуле (7.63). Отметим лишь, что они должны всегда образовывать невозрастающую с увеличением i последовательность, поскольку вес βM каждой порядковой статистики уменьшается.
В качестве примера приведем нормированные средние значения порядковых статистик x(i) при обнаружении ПРЦ с релеевским распределением амплитуд и при выбранных выше четырех типах априорных распределений числа элементов (рис. 7.36). Здесь число интервалов разрешения L = 16, число периодов N = 1, Mмакс = L. Наибольшее влияние уровня отношения сигнал/шум на вид зависимостей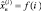 
наблюдается у малоэлементных ПРЦ, наименьшее – у многоэлементных ПРЦ. Абсолютные значения первых порядковых статистик x(1) практически пропорциональны отношению сигнал/шум.
а б в г
Рис. 7.36. Порядковые статистики при равномерном (а), многоэлементном (б), малоэлементном (в) и квазигауссовом (г) априорных распределениях
Зависимость коэффициента αi наглядно представлена на рис. 7.37 при двух значениях L. По оси ординат отложено значение lnαi, в обоих случаях Mмакс = L. С точностью до ошибок моделирования можно утверждать:
1) при обнаружении многоэлементной ПРЦ коэффициенты αi для любого отношения сигнал/шум должны быть одинаковыми, т. е. алгоритм с использованием порядковых статистик сводится к алгоритму аналогового накопления (см. 7.1);
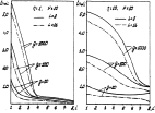
а б в г
Рис. 7.37 Зависимости коэффициента алгоритма (7.64) при равномерном (а), многоэлементном (б), малоэлементном (в) и квазигауссовом (г) априорных распределениях
2) в случае малоэлементной ПРЦ следует ограничиться только первой порядковой статистикой, поскольку коэффициент α2 при второй статистике меньше в exp(14/L) раз и алгоритм порядковых статистик сводится к алгоритму с выбором максимума;
3) при обнаружении ПРЦ с квазигауссовым априорным распределением следует учитывать только первые L/2 порядковых статистик с уменьшением от α1 до αL/2 примерно в e = 2,82 раз;
4) наконец, при обнаружении ПРЦ с равномерным распределением числа элементов необходимо использовать весь вариационный ряд, и коэффициенты αi при этом должны изменяться по закону
exp(–ai/L), где величина a зависит от отношения сигнал/шум, например, для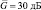 
значение a = 2,5, а для 
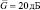оно равно единице.
Таким образом, алгоритм с использованием порядковых статистик в частных случаях может соответствовать рассмотренным выше алгоритмам с накоплением и выбором максимума, в общем случае он позволяет получить более высокую вероятность правильного обнаружения без изменения структуры алгоритма. Более того, если для некоторого значения отношения сигнал/шум, априорного распределения числа элементов ПРЦ и логарифма отношения правдоподобия lnB(y) рассчитать коэффициенты αi,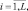 
как это сделано выше, то алгоритм с использованием порядковых статистик будет практически соответствовать оптимальному алгоритму обнаружения ПРЦ.
При этом по сравнению с оптимальным уменьшается объем вычислений, который здесь равен:
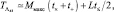
машинная память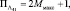 
но не преодолевается существенный недостаток, связанный с требованием априорного знания
g, P(M) и lnB(y).