Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.5.1. Комбинированный алгоритм с аналоговым накоплением и полным выбором максимума
Этот квазиоптимальный алгоритм представляет собой логическое объединение алгоритмов Λ10 и Λ30:
Λ50(y) = 1[Λ10(y) – T1] + 1[Λ30(y) – T2], (7.80)
где T1 и T2 – пороги первый и второй, Λ10(y) и Λ30(y) – первая и вторая статистики, вычисляемые согласно выражений (7.5) и (7.52) соответственно. Целочисленная статистика Λ50 может принимать три значения: 0, 1 и 2, и, если она отлична от нуля, то ПРЦ считается обнаруженной. Время на реализацию этого алгоритма на ЭЦВМ равно
,
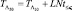машинная память занимает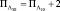 
ячеек.
Найдем характеристики обнаружения при одинаковых Pi,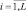 
и релеевской модели отраженных сигналов, обозначив n = NL. Вероятность ложной тревоги соответствует вероятности F = 1 – Pr (Λ10 < T1, Λ30 < T2). Характеристическая функция ограниченной экспоненциально распределенной случайной величины xi < T2 имеет вид:
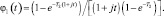(7.81)
Величина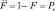 
(Λ10 < T1, Λ30 < T2) может быть найдена интегрированием обратного преобразования Фурье от n-й степени характеристической функции (7.81):
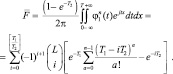
Итак, вероятность ложной тревоги равна:
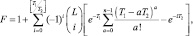(7.82)
где операция [x] означает взятие целой части от x.
Если порог T1 стремится к бесконечности (в частности T1 > nT2), то комбинированный алгоритм вырождается в алгоритм выбора максимума, если T2 стремится к бесконечности (в частности T2 > T1), то он соответствует алгоритму с аналоговым накоплением. Таким образом, выбором порогов T1 и T2 можно регулировать коэффициент участия статистик Λ10 и Λ30 в общей статистики обнаружения Λ50, изменяя его от нуля до единицы. В [2] приводится процедура SUMXIN, с помощью которой для заданных значений вероятности ложной тревоги и коэффициента участия можно вычислить оба порога. Вероятность правильного обнаружения находится методом, аналогичным использованному выше, и определяется формулой
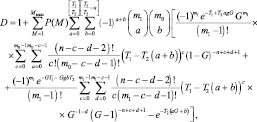(7.83)
где m1 = NM, m0 = N(L – M), n = NL, G = 1/(1 + g). Замечания по использованию этого выражения для расчета D те же, что были указаны в пункте 7.1.2 (см. выражение (7.18)).
На рис. 7.40 изображены характеристики обнаружения алгоритма (7.80), вычисленные методом статистического моделирования при одинаковых Pi. Число испытаний равно 1000. Пороги T1 и T2 в (7.80) выбраны такими, чтобы обеспечивались следующие соотношения между отдельными ветвями комбинированного алгоритма:
1) комбинированный полностью сводится к алгоритму с накоплением;
2) доля алгоритма с накоплением в комбинированном равна 0,7;
3) доля алгоритма с накоплением в комбинированном равна 0,5;
4) доля алгоритма с накоплением в комбинированном равна 0,3;
5) комбинированный полностью сводится к алгоритму с выбором максимума.
Как следует из анализа графиков, приведенных на крайних ситуаций – много- и малоэлементной ПРЦ – характеристики обнаружения комбинированного алгоритма занимают промежуточные положения по отношению к характеристики обнаружения алгоритмов с накоплением и выбором максимума. В целом, они лежат ближе к характеристикам того алгоритма, который является наилучшим из них для данной ситуации обнаружения. При этом максимальные потери комбинированного алгоритма по сравнению с наилучшим не превышают 0,5–0,8 дБ, в то время как выигрыш по сравнению с наихудшим может достигать 3,5–4,5 дБ. В наибольшей степени это свойство комбинированного алгоритма проявляется при средних отношениях сигнал/шум, когда не выполняются условия асимптотической близости к оптимальному алгоритмов с накоплением и выбором максимума. В некоторых случаях (равномерное распределение числа элементов ПРЦ, 
) комбинированный алгоритм обнаруживает ПРЦ с большей вероятностью, чем тот или иной из его составляющих (выигрыш до 0,5 дБ). Эти результаты говорят о том, что комбинированный алгоритм (7.80) может в значительной мере снизить, а иногда и устранить отрицательное влияние априорной неопределенности о числе элементов ПРЦ и отношении сигнал/шум на характеристики обнаружения. При этом наилучшее соотношение между составляющими комбинированного алгоритма лежит в области одинакового долевого участия в общем результате обнаружения, т. е. соотношение, примерно соответствующее названному выше случаю 3.
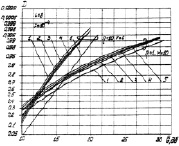
Рис. 7.40. Характеристики обнаружения алгоритма (7.80). Параметр – степень участия алгоритма с накоплением в общей статистике обнаружения
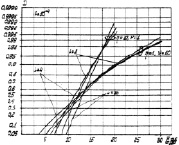
Рис. 7.41. Характеристики обнаружения алгоритма (7.80).
Параметр – число объемов разрешения
На рис. 7.41 представлены характеристики обнаружения в зависимости от параметра L – числа интервалов разрешения. Крутизна характеристик с увеличением L в целом растет. Граничное значение отношения сигнал/шум, выше которого возрастание L приводит к увеличению вероятности правильного обнаружения, а ниже – к её уменьшению, находится в диапазоне от 16 до 18 дБ.
Этот вывод относится также к характеристикам обнаружения ПРЦ с другими априорными распределениями числа элементов. В частности, характеристики обнаружения ПРЦ с равномерным распределением близки к таковым малоэлементной, а с квазигауссовым – к многоэлементной ПРЦ (рис. 7.42). Однако, как следует из рис. 7.41, при обнаружении малоэлементной ПРЦ однозначность увеличения D при возрастании L в диапазоне от 17 дБ до 23 дБ нарушена. На этом участке наибольшую вероятность правильного обнаружения обеспечивает обнаружитель с L = 8. Следовательно, свойство наличия оптимального числа интервалов разрешения алгоритмов (7.5) и (7.52), отмеченное в предыдущих параграфах, переносится и на комбинированный алгоритм.
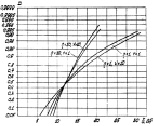
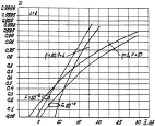
Рис. 7.42. Характеристики обнаружения алгоритма (7.80).
Параметр – тип априорного распределения
Рис. 7.43. Характеристики обнаружения алгоритма (7.80).
Параметр – вероятность ложной тревоги
Интересная особенность, относящаяся к обнаружению сложных целей любыми квазиоптимальными алгоритмами, отмечена на рис. 7.42. При указанных параметрах и отношении сигнал/шум 12 дБ комбинированный алгоритм имеет характеристики обнаружения, не зависящие от вида априорного распределения, т. е. в диапазоне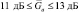 
они практически инвариантны к числу элементов ПРЦ. При увеличении L этот диапазон незначительно смещается в сторону возрастания 
,
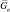например, при L = 16 он имеет границы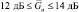 
. Подобное смещение существенно меньше, чем у алгоритмов (7.5) и (7.52), что говорит о бόльшей устойчивости характеристик обнаружения комбинированного алгоритма.
Представленные на рис. 7.43 зависимости вероятностей правильного обнаружения при различных порогах T (вероятностях ложной тревоги F) показывают, что с возрастанием T (уменьшении F) характеристики обнаружения практически параллельно переносятся в область бόльших значений отношений сигнал/шум.