
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.5.2. Комбинированные алгоритмы с аналоговым накоплением и межпериодным выбором максимума
При обнаружении дружно движущейся ПРЦ необходимо использовать в канале выбора максимума статистики, соответствующие сумме отсчетов за время наблюдения в L интервалах разрешения:
Λ52(y) = 1[Λ10(y) – T1] + 1[Λ32 (y) – T2], (7.84)
где Λ32(y) – статистика, определяемая согласно (7.57).
Решение о наличии ПРЦ принимается, если Λ51 отлично от нуля. Время на его реализацию на ЭЦВМ равно 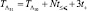 , необходимая машинная память составляет
, необходимая машинная память составляет 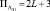 ячеек.
ячеек.
Из характеристик обнаружения удалось найти выражение для вероятности ложной тревоги при одинаковых значениях Pi. Характеристическая функция ограниченной случайной величины, имеющей гамма-распределение, равна
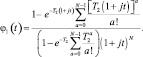 (7.84)
(7.84)
Величина F определяется соотношением
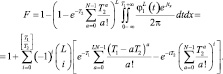 (7.49)
(7.49)
Как и в предыдущем алгоритме, выбором порогов T1 и T2 можно регулировать коэффициент участия статистик Λ10 и Λ32 в принятии решения об обнаружении ПРЦ. При T2 > T1 алгоритм (7.84) вырождается в алгоритм (7.5), при T1 > T2 он соответствует алгоритму с межпериодным выбором максимума (7.57). Процедура SUMSIN, с помощью которой для заданных значений F и F10 или F32 можно вычислить оба порога, приведена в [2].
При N > 2 в качестве первого приближения для вероятности правильного обнаружения следует использовать оценку снизу:
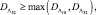 (7.50)
(7.50)
где вероятности правильного обнаружения 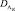 и
и 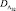 вычисляются соответственно по формулам (7.13) и (7.58) при подстановке в них порогов T1 и T2.
вычисляются соответственно по формулам (7.13) и (7.58) при подстановке в них порогов T1 и T2.
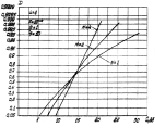
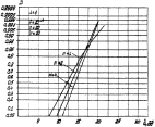
На рис. 7.44 приведены характеристики обнаружения комбинированного алгоритма (7.84), полученные методом статистического моделирования. Число испытаний равно 1000, полная энергия отраженных сигналов одинакова во всех ситуациях 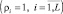 . С увеличением числа периодов повторения крутизна характеристик возрастает, причем поворот кривых наблюдается в области значений отношений сигнал/шум
. С увеличением числа периодов повторения крутизна характеристик возрастает, причем поворот кривых наблюдается в области значений отношений сигнал/шум 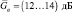 при малоэлементных ПРЦ и
при малоэлементных ПРЦ и 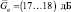 при квазигауссовом распределении числа её элементов. С ростом N вероятность правильного обнаружения для
при квазигауссовом распределении числа её элементов. С ростом N вероятность правильного обнаружения для 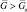 увеличивается. Например, выигрыш в отношении сигнал/шум на уровне D = 0,95 при N = 4 составляет 5 дБ по сравнению с N = 1 (рис. 7.44, а). Если
увеличивается. Например, выигрыш в отношении сигнал/шум на уровне D = 0,95 при N = 4 составляет 5 дБ по сравнению с N = 1 (рис. 7.44, а). Если 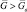 , то влияние числа периодов накопления N на характеристики противоположно.
, то влияние числа периодов накопления N на характеристики противоположно.
а б
Рис. 7.44. Характеристики обнаружения алгоритма (7.84)
при малоэлементном (а) и квазигауссовом (б) распределениях
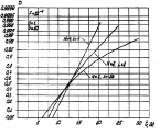
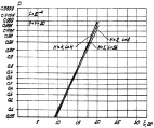
Интересный случай показан на рис. 7.45, где произведение числа интервалов разрешения на число периодов повторения равно постоянной величине – NL = 16. Общим является то, что при постоянном m = NL с увеличением N или L растет крутизна характеристик обнаружения. Различие состоит в том, что на этот рост существенное влияние оказывает распределение числа элементов ПРЦ: он наиболее заметен у малоэлементных и с равномерным распределением, наименее – у многоэлементных и с квазигауссовым распределением. В первом случае выигрыш в отношении сигнал/шум может достигать 5 дБ. Вместе с тем увеличение N, т. е. рассредоточение суммарной энергии зондирующего сигнала на большее число периодов повторения, приводит к увеличению времени обнаружения, а при малых отношениях сигнал/шум – к снижению качества обнаружения ПРЦ.
а б
Рис. 7.45. Влияние соотношения между числом объемов разрешения
и числом периодов повторения на характеристики обнаружения:
а – малоэлементное; б – квазигауссовое априорные распределения
Таким образом, при использовании комбинированного алгоритма (7.84) следует ограничить число периодов повторений десятью – шестнадцатью при соответствующем уменьшении числа объемов разрешения до четырех – двух. На предельных дальностях обнаружения РЛС энергию зондирующего сигнала необходимо сосредотачивать в одиночный импульс с объемом разрешения, приближенно совпадающим с объемом, занимаемом ПРЦ.
