Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.1.1. Оптимальный алгоритм выделения сигнальных дискретов
Предположим, что выполняется неравенство
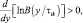
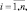
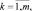(8.1)
которое означает математическую формулировку условия: большему по величине принятому отсчету соответствует большая вероятность того, что этот отсчет – сигнальный. Тогда, составив из всех принятых отсчетов вариационный ряд, для каждого из них можно ввести соответствующую вероятность – меру принадлежности отсчета сигналу, которая постоянно убывает при увеличении его номера в этом ряду. Если точно известно число M отраженных сигналов, то, при условии равновероятности расположения элементов сложной цели на радиолокационном поле, выделение сигнальных дискретов состоит в записи в соответствующий массив координат M первых дискретов вариационного ряда. Этот алгоритм означает, что в i-м канале на рис. 6.1 выбирается сумма, имеющая максимальное значение среди всех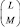 
сумм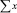 
(см. также формулу (6.13)). Следовательно, полученная таким образом дискретная модель является максимально правдоподобной оценкой радиолокационного изображения ПРЦ. В том случае, когда вероятности Pik,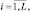 
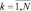расположения элементов ПРЦ на радиолокационном поле неодинаковы, необходимо строить вариационный ряд на основании апостериорной вероятности, т. е. использовать для ранжирования величину PiklnB(y/τik). Дискретная модель в этом случае является оценкой максимальной апостериорной вероятности. Неизвестность числа элементов сложной цели, не изменяя приведенных выше алгоритмов, требует введения дополнительного блока оценивания M. Структура этого блока, его характеристики подробно рассматривались в главе 6. Здесь отметим лишь то, что критерий оценивания M и дискретной модели радиолокационного изображения должны совпадать. Отметим также, что при условии выполнения неравенства
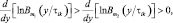m1 > m2, (8.2)
где m1 и m2 – число элементов ПРЦ в дискрете разрешения, можно получить дискретную модель при снятом предположении 1 в начале параграфа (см также параграф 6.2).
Наиболее существенным недостатком приведенного оптимального алгоритма являются большие вычислительные затраты на его реализацию. Чтобы сравнить их, необходимо обратиться к квазиоптимальным алгоритмам.