
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.1.2. Квазиоптимальный алгоритм выделения сигнальных элементов
При синтезе квазиоптимального алгоритма воспользуемся условием: в практически интересных случаях для получения качественных оценок отношение сигнал/шум не должно быть ниже некоторой величины. При этом условии число сигнальных дискретов редко достигает половины общего числа дискретов. Тогда оптимальный алгоритм выделения может быть заменен квазиоптимальным алгоритмом – подискретным сравнением всех отсчётов с некоторым заранее выбранным порогом T. Здесь наблюдается аналогия с алгоритмами обнаружения – оптимальным и выбором максимума (см. параграф 7.3).
Итак, квазиоптимальный алгоритм выделения сигнальных дискретов состоит в определении координат тех отсчетов, которые превысили порог T. Порог задается вероятностью ложной тревоги для одного дискрета разрешения.
Получим рекомендации по выбору порога. Назовем эталоном действительное расположение элементов ПРЦ на радиолокационном поле, а образом – полученное в результате выделения на фоне шумов. Общее среднее число несовпадений 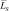 между эталоном и образом равно сумме среднего числа превышения
между эталоном и образом равно сумме среднего числа превышения 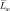 порога T шумом и не превышений
порога T шумом и не превышений 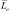 сигналом + шумом:
сигналом + шумом:
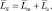 (8.3)
(8.3)
При использовании квазиоптимального алгоритма
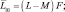
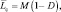 (8.4)
(8.4)
где L – общее число дискретов разрешения, L = nm; M – число сигналов; 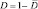 – вероятность правильного обнаружения отраженного сигнала в одном дискрете.
– вероятность правильного обнаружения отраженного сигнала в одном дискрете.
Для релеевской модели отраженного сигнала на выходе квадратичного детектора выражение (8.3) примет вид
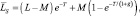 (8.5)
(8.5)
где T = –lnF – нормированный порог для одного дискрета.
Изменение отношения сигнал/шум не влияет на первое слагаемое в формуле (8.5), в то время как второе изменяется по экспоненциальному закону. Этот закон отчетливо проявляется на рис. 8.1, на котором показаны зависимости среднего числа несовпадений 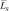 при L = 500, M = 111. Численные результаты получены путем статистического моделирования изображений при числе испытаний Q = 100 и Q = 1000. Графики отображают устойчивость результатов моделирования при Q > 100. При уменьшении F первое слагаемое уменьшается, доля его в
при L = 500, M = 111. Численные результаты получены путем статистического моделирования изображений при числе испытаний Q = 100 и Q = 1000. Графики отображают устойчивость результатов моделирования при Q > 100. При уменьшении F первое слагаемое уменьшается, доля его в 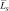 существенно падает и при F < 10–3 его можно не учитывать. Это говорит о том, что при L – M = 389 и F < 10–3 случайных превышений порога шумом практически не наблюдается.
существенно падает и при F < 10–3 его можно не учитывать. Это говорит о том, что при L – M = 389 и F < 10–3 случайных превышений порога шумом практически не наблюдается.
Таким образом, величину
Fгр = (L – M)–1 (8.6)
следует принять за граничную вероятность ложной тревоги, выше которой ещё сколько-нибудь заметна величина 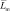 . Если F < Fгр, то Ls изменяется по экспоненциальному закону с показателем, равным
. Если F < Fгр, то Ls изменяется по экспоненциальному закону с показателем, равным 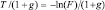 . Очевидно, при g > –Mln(F) = MT несовпадения между эталоном и образом практически не наблюдаются.
. Очевидно, при g > –Mln(F) = MT несовпадения между эталоном и образом практически не наблюдаются.

Рис. 8.1. Зависимости числа несовпадений от отношения сигнал/шум
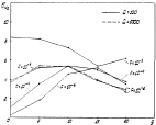
Рис. 8.2. Зависимости СКО числа несовпадений от отношения сигнал/шум
Определим вероятность ложной тревоги F0 и, тем самым, порог T0, при которых для заданной величины g среднее число несовпадений минимально. Дифференцируя (8.5) по T и решая полученное уравнение относительно T0 и F0, получим:
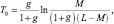
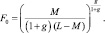 (8.7)
(8.7)
При средних и больших отношениях сигнал/шум (g > 10 дБ) можно принять
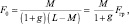 (8.8)
(8.8)
т. е. F0 практически одного порядка с Fгр.
Введением различных весов для слагаемых в (8.3) можно определить показатель несоответствия эталона и образа
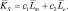 (8.9)
(8.9)
Тогда выражения (8.7) можно записать в более общем виде:
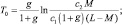
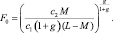 (8.10)
(8.10)
Найдем зависимости среднеквадратичных ошибок (СКО) величины 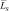 от g. Поскольку
от g. Поскольку 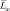 и
и 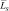 статистически независимы и могут интегрироваться как результат соответствующего числа испытаний Бернулли, то дисперсия
статистически независимы и могут интегрироваться как результат соответствующего числа испытаний Бернулли, то дисперсия 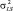 равна сумме дисперсий слагаемых:
равна сумме дисперсий слагаемых:
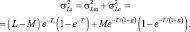 (8.11)
(8.11)
Наибольшее значение СКО имеет при отношении сигнал/шум
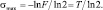 (8.12)
(8.12)
При этом значение СКО
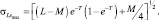 (8.13)
(8.13)
Если F < Fгр то первое слагаемое в (8.13) исчезает и максимальное значение СКО зависит только от числа элементов ПРЦ
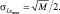 (8.14)
(8.14)
При F < Fгр СКО увеличивается незначительно (см. рис. 8.2.)
В заключение параграфа отметим следующее: чем больше элементов имеет сложная цель, тем меньше влияние разброса за счет шума на соответствие между образом и эталоном. Действительно, при правильно выбранных порогах относительное среднее число несовпадений 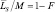 остается при увеличении числа элементов ПРЦ неизменным, а относительный разброс
остается при увеличении числа элементов ПРЦ неизменным, а относительный разброс 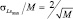 при этом уменьшается.
при этом уменьшается.
