Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.3. Анализ результатов статистического моделирования алгоритмов оценивания общегрупповых параметров ПРЦ
Алгоритмы оценивания, описанные выше, были исследованы в [13, 14] на двух примерах – малом (рис. 8.4) и большом (рис. 8.5) – построения эталона радиолокационного изображения при двух видах распределений амплитуд отраженных сигналов: релеевском (5.23) и обобщенном релеевском (5.24) на входе квадратичного детектора. В обоих примерах заданы по одной группе каждого класса, в зачерненных дискретах радиолокационный сигнал равен сумме отраженного сигнала и шума, а пустых – только одного шума. Вследствие приемлемых затрат машинного времени малый пример анализировался в более широком диапазоне изменения параметров, чем большой. Как правило, число испытаний Q было равно 100, в некоторых случаях оно выбиралось в 10 раз больше. Сравнение результатов, полученных в том и другом случае, привело к выводу, что при Q = 100 усредненные по числу испытаний характеристики алгоритмов оценивания общегрупповых параметров найдены с точностью, достаточной для проведения последующего анализа. На всех рисунках графики изображены в виде ломанных линий, состоящих из отрезков прямых, соединяющих вычисленные в эксперименте точки. Этот прием позволяет получить более наглядное графическое изображение исследуемых зависимостей при ограниченном числе экспериментальных точек.
При анализе алгоритмов оценивания общегрупповых параметров использовались следующие характеристики групп и классов:
1. Абсолютные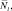 
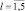и относительные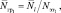 
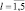, средние значения числа обнаруженных групп в каждом классе.
2. Вероятность необнаружения 
групп l-го класса.
3. Среднее отклонение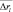 
общегруппового параметра обнаруженной группы l-го класса от действительного параметра, задаваемого эталоном.
4. Среднее число Ml1 ненулевых дискретов группы l-го класса.
5. Среднее число несовпадений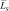 
дискретов разрешения между эталоном и образом (см. пункт 8.1.2).