
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.3.1. Сравнение оптимального и квазиоптимального алгоритмов выделения сигнальных дискретов
Оптимальный алгоритм синтезирован для выделения всей совокупности сигнальных дискретов, и в этом смысле он придает каждому из них одинаковые веса (см. условие 1 параграфа 8.1). При группировании эта равноценность дискретов приводит к неодинаковому участию групп различных классов в общей статистике оценивания числа сигнальных дискретов, определяемого числом дискретов групп. Следовательно,
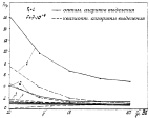
оптимальный алгоритм выделения сигнальных дискретов в большей степени настроен на распознавание групп старших классов. Однако, выбрав некоторое значение вероятной ложной тревоги F*, близкое к F0, можно получить более качественные характеристики распознавания групп младших (первого, второго, частично третьего) классов, если в некоторой мере снизить требования к качеству распознавания групп старших классов. С увеличением отношения сигнал/шум влияние подобного приема на характеристики уменьшается и уже при g > 15 дБ оно практически незаметно. Эти общие положения наглядно иллюстрируются рис. 8.6, на котором представлены результаты моделирования обоих алгоритмов при обработке образа малого примера. Следует отметить, что время моделирования при использовании оптимального алгоритма в 11,3 раза больше, чем квазиоптимального. Во втором случае величина F выбрана такой, которая обеспечивает наилучшее качество распознавания групп всех классов.

а б
Рис. 8.6. Сравнение характеристик оценивания числа групп при различных межгрупповых расстояниях:
а – r0 = 1; б – r0 = 2,5
Сравнение графиков зависимостей приводит к следующим выводам:
а) применение оптимального алгоритма выделения сигнальных дискретов может быть рекомендовано при распознавании групп старших классов, то есть ПРЦ с числом элементов более 5–10, при малых отношениях сигнал/шум (g < 10 дБ). При этом межгрупповое расстояние должно быть задано в диапазоне (2–3) дискрета;
б) в остальных случаях необходимо использовать квазиоптимальный алгоритм выделения сигнальных дискретов при соответствующих значениях вероятности ложной тревоги F* и межгрупповом расстоянии 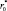 .
.
Итак, наибольший практический интерес представляют характеристики оценивания квазиоптимального алгоритма, результаты анализа и рекомендации по выбору параметров F* и 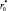 которого приводятся ниже.
которого приводятся ниже.
