
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.3.2. Характеристики оценивания при использовании квазиоптимального алгоритма выделения сигнальных дискретов и релеевской модели отраженного сигнала
На рис. 8.7 представлены зависимости вероятности необнаружения групп различных классов в малом примере для крайних значений вероятностей ложной тревоги F = 10–1 и F = 10 –6 (r0 =1).

Рис. 8.7. Зависимости вероятности необнаружения групп в малом примере от отношения сигнал/шум
Группы, относящиеся к более старшему классу, обнаруживаются, в основном, хуже по сравнению с группами младших классов. При малых F Fгр увеличение отношения сигнал/шум g приводит к тому, что величина D возрастает, но для групп младших классов от 10 до 15 дБ происходит ухудшение обнаружения. При таких отношениях сигнал/шум начинают обнаруживаться группы старших классов (четвертого и пятого), которые ранее, при малых g, были раздроблены и воспринимались как группы младших классов. При уровне g выше 15 дБ все классы имеют тенденцию к улучшению качества обнаружения.
Для больших вероятностей ложной тревоги (F > Fгр) младшие классы хорошо обнаруживаются во всем диапазоне отношений сигнал/шум, а все классы – начиная с уровня 8–9 дБ. Отличительной особенностью этого случая является не очень высокое качество обнаружения групп третьего класса. Для всех вероятностей ложных тревог 10–1 ≤ F ≤ 10–6 группы пятого класса, начиная с некоторого g, обнаруживаются с вероятностью, близкой к единице, например, при F = 10–1 – с 10 дБ и выше, а при F = 10–6 – с 15 дБ.
Зависимости вероятности необнаружения групп от уровня F при фиксированном отношении сигнал/шум (g =5 дБ), представленные на рис. 8.8 также показывают увеличивающуюся с возрастанием номера класса вероятность необнаружения. При малых F появляются случаи необнаружения групп даже первого класса. При больших F группы пятого класса обнаруживаются лучше, чем группы четвертого класса. Это происходит вследствие большого числа шумовых ненулевых элементов разрешения, которые объединяются в группы сверхбольшого размера. Теснота расположения групп на информационном поле приводит к тому, что некоторые группы объединяются за счет ненулевых шумовых элементов и переходят в другой класс. Следовательно, вероятность ложных тревог F* для малого примера должна быть не выше Fгр, в противном случае группы старших классов обнаруживаются за счет групп младших классов. К аналогичному выводу приводит анализ характеристик оценивания в большом примере.
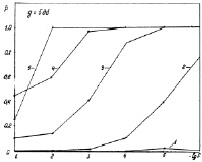
Рис. 8.8. Зависимости вероятностей необнаружения групп от вероятности ложной тревоги в малом примере
Разница в пороговом сигнале при одних и тех же условиях обнаружения наиболее значительна между первым и вторым классами, на уровне D = 0,8, F = 10–6 она равна (5–6) дБ. Чуть меньше различие наблюдается между вторым и третьим, а также четвертым и пятым классами.
Определенный интерес вызывают зависимости вероятности необнаружения групп от номера класса, построенные для малого примера на рис. 8.9. При малых отношениях сигнал/шум (0–5 дБ) наблюдается в среднем ухудшающееся качество обнаружения групп с возрастанием номера класса (от единицы для первого до нуля для пятого). При средних и больших отношениях сигнал/шум наиболее примечательно плохое качество обнаружения групп четвертого класса. Например, при g ~ (10–15) дБ вероятность обнаружения группы четвертого класса равна 0,4, а при g ~ (15–20) дБ – 0,8, в то время как другие классы имеют вероятность обнаружения не хуже 0,95 (рис. 8.9, а).


а б
Рис. 8.9. Зависимости вероятности необнаружения группы от номера класса в малом примере:
а – F = 10–2; б – F = 10–4
При уменьшении вероятности ложной тревоги с 10–2 до 10–4 (см. рис. 8.9, б) четвертый класс уже не так выделяется на фоне других классов, особенно для больших и малых отношений сигнал/шум. Значительно хуже обнаруживаются группы первого класса, происходит естественный сдвиг всех зависимостей влево от старших классов к младшим.
Отличие большого примера от малого состоит в том, что в этом случае при тех же параметрах наихудшим качеством обнаружения обладают группы третьего класса. Такой переход от четвертого к третьему классу объясняется гораздо меньшим влиянием межгрупповых расстояний в большом примере на группировку ненулевых дискретов при F > Fгр. При уменьшении вероятности ложной тревоги (F < Fгр) этот эффект, как и в малом примере, исчезает. Таким образом, вероятность обнаружения группы существенно зависит от вероятности ложной тревоги для одиночного сигнала, которая должна выбираться не больше Fгр. В противном случае резко уменьшается вероятность обнаружения групп третьего и четвертого, т. е. средних классов. Если же F < Fгр, то, как правило, наихудшее качество обнаружения при средних отношениях сигнал/шум имеют группы первого и четвертого-пятого классов. При малых отношениях сигнал/шум (g = 0–10 дБ) группа обнаруживается тем хуже, чем больше номер ее класса, при больших (g > 20 дБ) – группы всех классов обнаруживаются практически всегда.
Рассмотрим, как влияют параметры обнаружения F и g на количество обнаруживаемых групп в обоих примерах. В малом примере при F > Fгр число обнаруженных групп первого и второго классов велико и с возрастанием отношения сигнал/шум ниже некоторых значений не уменьшается. Для первого класса это значение равно 15,6, для второго – 4,8, для третьего – 1,5 (рис. 8.10). Поскольку дополнительные группы возникают при больших g только за счет шума, то можно сказать, что примерно половина шумовых ненулевых отсчетов, среднее число которых в этом случае равно 38.9, идет на формирование групп первого класса, столько же – на формирование групп второго класса и примерно 10 % – на группы третьего класса. По этой же причине СКО числа таких групп не зависит от g, как это показано на рис. 8.11 (F = 10–1) штриховыми линиями. Даже число групп четвертого класса при такой большой ложной тревоге имеет смещенное выборочное среднее, а его СКО также постоянно при больших g. Группы пятого класса обнаруживаются точно, начиная с g = 10 дБ. При малых отношениях сигнал/шум наибольшее число групп имеют младшие классы, а наименьшее – старшие классы.


Рис. 8.10. Зависимости среднего числа групп в классе от отношения сигнал/шум в малом пример
Рис. 8.11. Зависимости СКО среднего числа групп в классе от отношения сигнал/шум в малом примере
При F < Fгр резко изменяется количество обнаруженных групп и их зависимость от отношения сигнал/шум. Для первого класса при g =5 дБ оно уменьшается, например в 2,5 раза. Начиная с g = 10 дБ при его дальнейшем увеличении число групп стремится к истинной величине, а при g > 15 дБ оно практически равно ей для всех классов, кроме четвертого (см. рис. 8.10). СКО среднего числа групп также стремится в этом случае (F = 10–4) к своему асимптотическому значению – нулю – и при g > 15 дБ не превышает 0,8, а при g > 20 дБ – 0,3.
Наибольшее лишнее число групп обнаруживается при отношениях сигнал/шум от 5 до 10 дБ. В этом диапазоне алгоритмам группирования и классификации работать наиболее трудно: вследствие небольшого отношения сигнал/шум группы четвертого и пятого классов обнаруживаются плохо, они дробятся на отдельные небольшие скопления, которые воспринимаются алгоритмом как группы меньших классов, группы третьего и второго классов по этой же причине обнаруживаются как группы второго или первого класса или вообще не обнаруживаются. Происходит переход групп из того класса, к которому они действительно принадлежат, к классам меньших номеров, что приводит к перепутыванию и наложению характеристик обнаружения и классификации. Подобное явление будет наблюдаться при любой вероятности ложной тревоги F* < Fгр, но при различных отношениях сигнал/шум, особенно для первого класса.
Этот вывод подтверждается зависимостями среднего числа групп в классе от отношения сигнал/шум в большом примере, изображенными на рис. 8.12. Здесь при уменьшении F с 10–4 до 10–6 отношение сигнал/шум, при котором число групп первого класса максимально, увеличилось с 5 дБ до 10 дБ, причем само это максимальное число изменилось незначительно – с 9,5 до 8,2. На других классах уменьшение F сказалось еще в меньшей степени. Отметим, что максимальное число групп как первого, так и второго классов при одинаковой вероятности ложной тревоги (F = 10–4 < Fгр) для малого и большого примеров остается примерно одинаковым, соответственно 7,8 и 9,5, 3,0 и 4,8, хотя общие размеры радиолокационного изображения увеличились в 6 раз.
Таким образом, при F < Fгр среднее число обнаруженных групп практически не зависит от размеров радиолокационного изображения и целиком определяется при малых и средних отношениях сигнал/шум размерами и конфигурацией групп. Изменение F в диапазоне (0, Fгр) почти не сказывается на количественных соотношениях между средним числом m групп обнаруживаемых классов, приводя лишь к смещению по оси отношений сигнал/шум характеристики оценивания. Следовательно, выбор очень низкой вероятности ложной тревоги с точки зрения наилучшего соответствия числа обнаруженных групп действительному не оправдан. Величина её должна быть примерно одного порядка с Fгр.


Рис. 8.12. Зависимости среднего числа групп в классе от отношения сигнал/шум в большом примере
Рис. 8.13. Зависимости средней ошибки определения общегруппового параметра от отношения сигнал/шум в большом примере
Рассмотрим зависимости средней ошибки определения общегруппового параметра 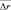 , представляющего, как было сказано ранее, отклонение от центра тяжести группы, от отношения сигнал/шум и номера класса. Величина
, представляющего, как было сказано ранее, отклонение от центра тяжести группы, от отношения сигнал/шум и номера класса. Величина 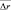 на графиках имеет размерность дискрета разрешения. Приведенные на рис. 8.14 характеристики говорят о том, что при большой вероятности ложной тревоги F > Fгр и увеличении отношения сигнал/шум ошибка
на графиках имеет размерность дискрета разрешения. Приведенные на рис. 8.14 характеристики говорят о том, что при большой вероятности ложной тревоги F > Fгр и увеличении отношения сигнал/шум ошибка 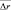 у групп всех классов не уменьшается, а у некоторых классов даже возрастает. Не уменьшается с увеличением сигнал/шум и СКО средней ошибки, например, его значение велико (даже аномально) у групп второго класса. Шумовые выбросы при большой ложной тревоге, помогая раньше обнаружить группы, не позволяют достаточно точно определить их местоположение.
у групп всех классов не уменьшается, а у некоторых классов даже возрастает. Не уменьшается с увеличением сигнал/шум и СКО средней ошибки, например, его значение велико (даже аномально) у групп второго класса. Шумовые выбросы при большой ложной тревоге, помогая раньше обнаружить группы, не позволяют достаточно точно определить их местоположение.
Уменьшение вероятности ложной тревоги (F < Fгр), приводит, естественно, к резкому возрастанию средних ошибок определения общегруппового параметра 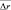 при малых отношениях сигнал/шум. Однако в этом случае существенно уменьшаются ошибки
при малых отношениях сигнал/шум. Однако в этом случае существенно уменьшаются ошибки 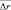 при больших отношениях сигнал/шум.
при больших отношениях сигнал/шум.
Например, при F = 10–4 и g = 15 дБ величина 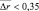 , а при g = 20 дБ практически равна нулю для всех классов, т. е. местоположение групп определяется точно. Этот вывод также подтверждают зависимости СКО при F = 10–4, показанные на рис. 8.15 сплошными линиями, сходящимися практически к нулю при g ≥ 20 дБ. Дальнейшее уменьшение F (F Fгр) не приводит к существенному изменению зависимости средних ошибок
, а при g = 20 дБ практически равна нулю для всех классов, т. е. местоположение групп определяется точно. Этот вывод также подтверждают зависимости СКО при F = 10–4, показанные на рис. 8.15 сплошными линиями, сходящимися практически к нулю при g ≥ 20 дБ. Дальнейшее уменьшение F (F Fгр) не приводит к существенному изменению зависимости средних ошибок 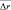 , лишь в небольшой степени поднимая их на одинаковую величину при всех отношениях сигнал/шум.
, лишь в небольшой степени поднимая их на одинаковую величину при всех отношениях сигнал/шум.

Рис. 8.14. Зависимости средней ошибки определения общегруппового параметра от отношения сигнал/шум в малом примере

Рис. 8.15. Зависимость СКО определения общегруппового параметра от отношения сигнал/шум в малом примере
Сравнение малого (см. рис. 8.14) и большого (см. рис. 8.13) примеров приводит к следующим общим выводам: при F < Fгр группы первого класса обнаруживаются на своих действительных местах достаточно точно при отношениях сигнал/шум g > 15 дБ 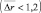 , группы второго, третьего и четвертого классов – начиная с 10 дБ
, группы второго, третьего и четвертого классов – начиная с 10 дБ 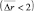 , а группы пятого класса – с 15 дБ. Пятый класс отличается тем, что, если группы этого класса обнаружены, то это наверняка группы пятого класса с тем же самым общегрупповым параметром. Таким образом, и с точки зрения наименьшей ошибки в определении общегруппового параметра вероятность ложной тревоги F должна быть ниже Fгр и не очень существенно отличаться от неё. При выполнении этого условия группы всех классов имеют ошибку
, а группы пятого класса – с 15 дБ. Пятый класс отличается тем, что, если группы этого класса обнаружены, то это наверняка группы пятого класса с тем же самым общегрупповым параметром. Таким образом, и с точки зрения наименьшей ошибки в определении общегруппового параметра вероятность ложной тревоги F должна быть ниже Fгр и не очень существенно отличаться от неё. При выполнении этого условия группы всех классов имеют ошибку 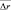 при g = 15 дБ меньше 1,7, при g = 20 дБ – меньше 0,8 дискрета.
при g = 15 дБ меньше 1,7, при g = 20 дБ – меньше 0,8 дискрета.
Границами изменения величины r0 в алгоритме «ближнего соседа» являются единица и минимальное межгрупповое расстояние, которое априори, как правило, неизвестно. Выбор того или иного значения 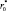 в этом диапазоне при соответствующем подборе вероятности ложной тревоги F* практически не сказывается на характеристиках оценивания. Поэтому, не рассматривая подробно результаты исследований, приведем окончательные рекомендации по выбору параметров
в этом диапазоне при соответствующем подборе вероятности ложной тревоги F* практически не сказывается на характеристиках оценивания. Поэтому, не рассматривая подробно результаты исследований, приведем окончательные рекомендации по выбору параметров 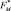 и
и 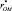 в малом примере (табл. 8.1). При анализе других изображений переход должен выполняться по формулам
в малом примере (табл. 8.1). При анализе других изображений переход должен выполняться по формулам
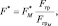
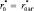 (8.18)
(8.18)
Таблица 8.1
Настраиваемые параметры квазиоптимального алгоритма выделения ПРЦ
