
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования
Портнягин Н. Н., Пюкке Г. А.,
2.4. Минимаксный критерий эквидистантности изовар
Комплексный критерий Z формируется по принципу 10% -го отбора подмножества М1 пар коэффициентов передачи по признаку максимального Zпри возрастании математического ожидания и убывании среднеквадрати ческого отклонения интегральной чувствительности каналов. Количество пар каналов, подлежащих исследованию при отборе, определяется комбинаторно: R = С М2 , где М – количество функций передачи возможных для диагностируемой электрической цепи. Критерий Z используется для первоначального отбора подмножества пар функций передачи в интервале десяти процентов от максимального значения Z при двумерном прямом переборе всех сочетаний функций передачи, имеющих максимальную чувствительность и минимальный разброс чувстви тельности по изоварам.
Минимаксный критерий, используемый для отбора пар функций передачи, удовлетворяющих условию эквидистантности изовар позволяет отсеять каналы, порождающие совпадающие и близко расположенные друг к другу изовары. Механизм реализации критерия состоит в первоначальном определении для каждой пары отношения чувствительностей Δ Ki(N) / Δ Kj(N) минимальной разности углов ¦φ k – φN ¦, (N = 1, (m – 1); K = N + 1, m – количество изовар) между изоварами, с последующим отбором пары (Δ K i , Δ K j), имеющей максимальное значение разности ¦φ i – φ j¦ из всех минимальных, определенных ранее. Углы измеряются на интервале [- π/2; π/2]. Критерий задается в точке ра вновесия (при номинальных значениях параметров СЕ). Приращения Δ K i и Δ K j (Рис. 2.15) определяются в точке равновесия при одних и тех же приращениях параметров Δ g для различных изовар и различных пар сочетания каналов.
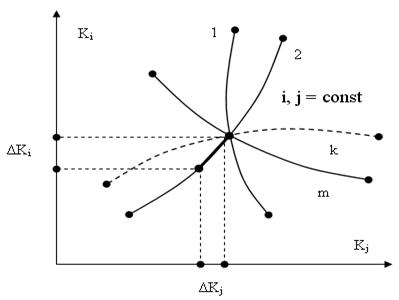
Рис. 2.15. К критерию эквидистантности
Каждое сочетание Δ Ki / Δ Kj в результате критериальной оценки дает “m” углов направления изовар в точке равновесия:
θ ω = arctg ( Δ Ki(ω) / Δ K j(ω) ¦i, j = constω = 1, m ,
где θ ω - угол между направлением касательной к изоваре в точке равновесия и положительным направлением оси абсцисс (рис. 2.15). Это дает возможность построить (m-1) углов θ N k между соседними изоварами, оценить их величины и зафиксировать минимальный:
θN k min.. θ N k = ¦φ k –φ N ¦= arctg (Δ K i( k) / Δ K j( k ) ) – arctg (Δ K i( N ) / Δ K j( N ) ); N = 1, m ; k = N + 1
В процессе рассмотрения различных пар сочетания каналов, находится пара функций передачи, обеспечивающая максимально возможную нижнюю границу множества значений углов для данного ОД:
θ i j max = max { min { ¦φ k – φ N ¦k = N + 1N = 1, m j = const i = const } ¦j = vari = var ,
где N, k – номера изовар. i, j – номера отбираемых функций передачи. Результатом такого отбора является гарантия того, что в семействе изовар, построенных на основе отобранной пары каналов, все углы расхождения в точке равновесия будут больше отобранного по критерию угла, что обеспечит удовлетворительную разрешающую способность при диагностировании. Результатом исполнения введенного критерия является выбор, из ранее отобранного по критерию Z подмножества М1, пары функций передачи, удовлетворяющей условию эквидистантности. Если подмножество М1 не содержит пары функций передачи, удовлетворяющей второму критерию, то анализируется следующее подмножество М2, отобранное в интервале от десяти до двадцати процентов от максимального значения Z из упорядоченного множества М и т. д. Процедура выполняется до тех пор, пока ни будут обнаружены оптимальные каналы прохождения тестового сигнала в соответствие с выбранными ограничениями на численные значения критериев: Z ≥Zmin , θ i j = ≥ θ i j min Значения Zmin и θ i j min задаются из условий допустимых погрешностей на измерения и вычисления. При машинной обработке данных используется два цикла перебора: 1. По верхним индексам, для определения минимального для данного сочетания функций передачи значения угла θ N k min (нижние границы). 2. По нижним индексам для определения номеров каналов, имеющих наибольшие нижние границы.
Необходимость введения критерия близости точка равновесного состояния к середине первого квадранта (точка с координатами ( 0,5; 0,5)) обусловлена процессом вырождения изоварной картины при приближении точки равновесия к границам пространства диагностирования. Положение точки равновесия в пространстве диагностирования зависит не только от топологии диагностируемой электрической цепи и номиналов составляющих компонент, изменять величины которых невозможно, но и от выбора каналов прохождения тестового сигнала, выполняя который, можно подобрать оптимальную изоварную картину. Нами разработан комплексный алгоритм разработки диагностического обеспечения и написан пакет программаMATRIX (Рис. 2.16),
 .
.
Рис. 2.16. Экранная форма окна «О программе»
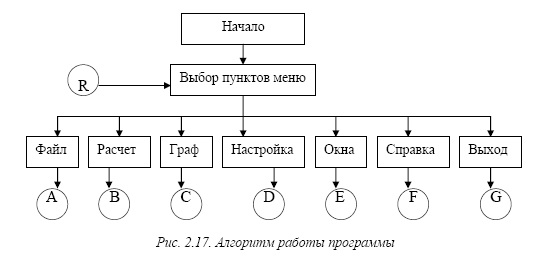
позволяющий по исходным данным (топологический граф, параметры составляющих компонент) вычислять топологические матрицы, производить отбор основных диагностических признаков по оптимизационным критериям и строить изоварную картину в пространстве диагностирования. Общий алгоритм работы программы представлен на рис. 2. 17. Проектирование структуры данных начинается с анализа информации о размерности матрицы инциденций и значений ее коэффициентов, размерности диагональной матрицы проводимостей компонент и значений ее коэффициентов.
 .
.
Сохранение построенных пользователем топологических графов выполняется с помощью класса Tstring List, который используется в качестве контейнера объектов. Проектируется структура данных для расчета и хранения информации по одному каналу, предназначенная для работы с матрицей узловых проводимостей и структура для хранения и расчета по двум каналам, предназначенная для работы с матрицей узловых проводимостей, сформированная из отдельных каналов после отбора по оптимизационным критериям. Алгоритм решения задачи отбора по оптимизационным критериям и его общая структура приведена на рис. 2.18.

Рис. 2.18. Общая структура алгоритма В