Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования

Портнягин Н. Н., Пюкке Г. А.,

2.5. Аналитическая диагностико-регулировочная модель электрической цепи, описанная на базе детерминированных процессов

Выбранные (на основе описанных выше критериев) диагностические признаки и диагностируемые параметры объединяются в единой диагностико – регулировочной модели, аналитически связывающей совокупность диагностических признаков, измеряемых непосредственно на ОД без нарушения топологии цепи с множеством диагностируемых параметров значения которых измерить невозможно без нарушения целостности структуры контролируемого ОД. При дальнейшем развитии обозначенного направления с последующим усложнением условий диагностирования и характера самого ОД возможно развитие новой методики разрешения задач поиска дефектов в разветвленных электрических цепях и определения степени работоспособности ОД. Описание алгоритма построения диагностической модели целесообразно начинать с рассмотрения примера простых резистивных электрических цепей с последующим усложнением задачи при использовании частотнозависимых и нелинейных элементов.

Построение диагностико-регулировочной модели выполняется методом исключения варьируемого параметра (диагностируемый параметр g_i) из совокупности уравнений, выражающих функции передачи (диагностические признаки) выбранных каналов прохождения тестового сигнала.

Т_{ав – cd} = f₁(g₁, g₂, ……,g_m);

Т_{kp – hl} = f₂ (g₁, g₂, ……,g_m).  (2.1)

где ав, кр – номера входных полюсов каналов прохождения тестового сигнала; cd, hl – номера выходных полюсов каналов прохождения тестового;

Т_{ав – cd} , Т_kp – hl – функции передачи каналов диагностирования; g₁, g₂, ……,g_m – совокупность диагностируемых параметров. В рамках линейной модели можно показать, что между множеством значений каждого из варьируемых параметров g₁, g₂, ……,g_m и совокупностью точек двумерного пространства диагностических признаков существует взаимно – однозначное соответствие. где Δ – шаг изменения значения диагностируемого параметра. Верхний индекс функции передачи соответствует номеру исключенного параметра (Рис. 2.19). Полученное соответствие дает возможность построить модель

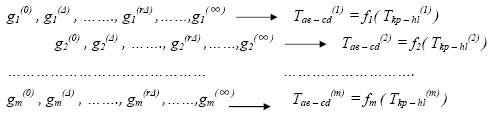
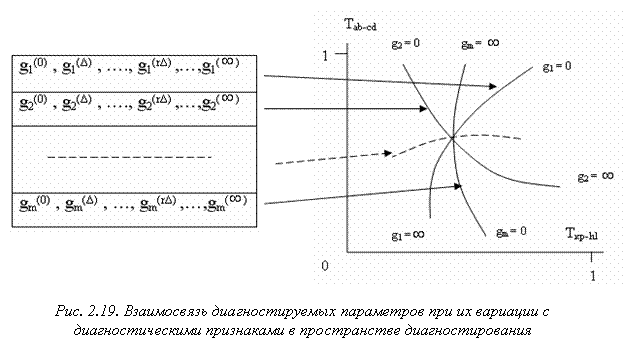
диагностирования, используемую для внедрения новой методики диагностирования разветвленных электрических цепей. В двумерном пространстве диагностирования {Т_{ав – cd} , Т_kp – hl } система изоварных характеристикгеометрически изображается совокупностью линий (Рис.2.19), пересекающихся в одной общей точке, координаты которой соответствуют числовым значениям диагностических признаков Т_{ав – cd}^* и Т_kp – hl^* при номинальных значениях диагностируемых параметров g_i (точка равновесия, соответствующая работоспособному  состоянию ОД S₀ ).  Для  электрических  цепей  любой топологии  в общем случае всегда дробно-линейные или линейные соотношения относительно варьируемого параметра, коэффициенты которых есть постоянные величины (в более общем случае рассмотренные коэффициенты суть рациональные функции комплексного параметра). Следует отметить, что при изменении диагностируемого параметра в пределах от 0 до  диагностические признаки всегда изменяются в конечных пределах, что обеспечивает сходимость процесса построения диагностической модели. Алгоритм построения диагностико – регулировочной модели состоит из следующих этапов:

1. Формирование массива основных диагностических признаков ОД, представленного в виде n – полюсной системы

Т₁ = f₁ (g₁, g₂, …….g_m);

Т₂ = f₂ (g₁, g₂, …….g_m);

……………………….

Т_M = f_M (g₁, g₂, …….g_m).

где М = С_n² (С_n² – 1) – общее количество каналов потенциально возможных для диагностирования; n – количество полюсов многополюсной системы; С_n² – число сочетаний из n элементов по два.

2. Выбор по назначенным критериям двух оптимальных каналов прохождения тестового сигнала с функциями передачи Т_{ав – cd} и Т_kp – hl .

Т_{ав – cd}  = f^* (g₁, g₂, …….g_m);

Т_{kp – hl} = f^** (g₁, g₂, …….g_m).

3. Формирование соотношений зависимости выбранных функций передачи от величины варьируемых параметров.

Т_{ав – cd}  = F₁ (g_m);  Т_{ав – cd}  = F₂ (g_m-1);…….. Т_{ав – cd}  = F_m (g₁)

Т_kp – hl = H₁ (g_m);  Т_kp – hl = H₂ (g_m-1);…….. Т_kp – hl = H_m (g₁).    (2.2)

4. Поэтапное исключение варьируемых параметров g_i из совокупности систем (2.2) Т_{ав – cd}  = G₁ (Т_kp – hl ); 

Т_{ав – cd}  = G₂ (Т_kp – hl );

…………………….

Т_{ав – cd}  = G_m (Т_kp – hl ).  (2.3)

Полученная система (2.3) связывает основные диагностические  признаки  Т_{ав – cd} и Т_kp – hl при вариациях параметров g₁, g₂, …….g_m на интервале [0, ).  При рассмотрении в качестве Т_{ав – cd} и Т_kp – hl только безразмерных функций цепи (например, коэффициент передачи по напряжению) можно обосновать достаточность использования только двух каналов диагностирования из всей совокупности функций передачи порождаемых многополюсной системой. Известно, что каждому фиксированному вектору диагностируемых параметров g₁^*, g₂^*, …….g_m^* будет соответствовать единственное значение функции передачи (диагностического признака) выбранного канала. Обратное утверждение не выполняется, действительно, численное значение функции передачи данного канала может достигаться при различных наборах значений диагностируемых параметров. Это можно показать аналитически, получив совпадающие значения функций передачи при различных вариациях диагностируемых параметров. Использование двумерного пространства диагностирования {Т_{ав – cd} , Т_kp – hl } обеспечивает однозначность соответствия паре значений координат (Т_{ав – cd} , Т_kp – hl ) единственного вектора значений диагностируемых параметров. Общность такого рассуждения следует из существования для произвольной n – полюсной системы в пространстве диагностирования несовпадающих наборов значений диагностических признаков при вариации параметров различных составляющих компонент. Так как каждый график является геометрическим местом точек, координаты которых соответствуют значениям функций передачи Т_{ав – cd} , Т_kp – hl при вариации одного из параметров g_i в интервале от нуля до бесконечности, то при отклонении значений параметров любой СЕ от номинального значения точка равновесного состояния переместиться по соответствующей кривой, что позволит идентифицировать соответствующую структурную единицу. Все промежуточные значения g_i будут соответствовать частичному изменению величины диагностируемого параметра.