Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования

Портнягин Н. Н., Пюкке Г. А.,

3.2. Коррекция аналитической модели диагностирования по выборке опытных данных

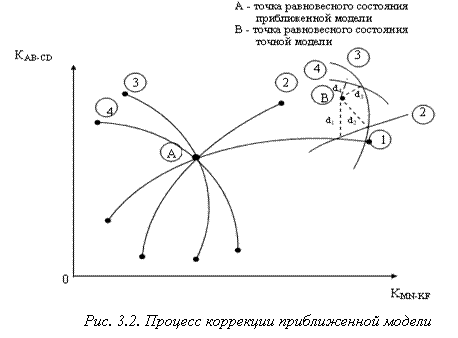
При построении диагностической модели ОД разработчик располагает приближенной информацией о величине параметров СЕ, что недостаточно для повышения точности. Выполнить точное поэлементное измерение номиналь ных значений параметров резистивных элементов (резисторы, конденсаторы, катушки индуктивности), не нарушая целостности ОД, не представляется возможности. Существующие же допуски на номинальные значения парамет ров не удовлетворяют условиям оценки. Определение параметров нелинейных взаимозависимых элементов представляет еще более трудоемкую задачу. Отсутствие информации о распределении потенциалов по узлам диагностируемой цепи, при подаче тестового сигнала, не дает возможности априорного определения полярности и величины тестового сигнала на р-n переходе рассматриваемой компоненты цепи. Это не позволяет определить положение рабочей точки, от которого будет зависеть величина дифференциального параметра. Справочные же данные вычисляются при опре деленном способе включения полупроводникового прибора и в рабочем режиме, обеспечение которого при воздействии только одного тестового сигнала, невозможно. Поэтому модель, построенная на основе приближенных значений параметров компонент ОД, нуждается в уточнении, а приближенные значения параметров компонент в корректировке. Для уточнения численных значений параметров СЕ используется метод постепенных приближений точки равновесного состояния приближенной модели к точке, координаты которой определя ются на реальном ОД измерением значений прямых диагностических признаков. Координаты точки равновесного состояния приближенной модели определяются расчетным путем при подстановке в уравнения модели прибли женных значений диагностических параметров (Рис. 3.2).

Численных значений диагностических признаков, могут быть заданы параметрически:

 К₁ = F(g₁,g₂,……,g_m);К₂ = F(g_1,g₂,……,g_m).  (3. 3)

Попеременное фиксирование в системе (3. 3) параметров в различных их сочетаниях позволяет получить параметрически заданное семейство изовар:

  К₁=F₁(g₁);  К₁=F₂(g₂);……….К₁=F_m(g_m).

   К₂=F₁(g₁); К₂=F₂(g₂);………. К₂=F_m(g_m).    (3. 4)

Cуть метода коррекции состоит в следующем: Сначала первая система (3. 4) исследуется  по  критерию  минимального  расстояния d,  при  вариации параметра g₁:

 min (d = [К_{2 изм} - К₂(g_i)]² + [К_{1 изм} - К₁(g_i)]²,   (3. 5)

где К_{1 изм}, К_{2 изм} – координаты точки равновесного состояния, измеренные на ОД; К₂(g_i), К₁(g_i) – текущие координаты точки равновесного состояния приближенной модели; g_i – варьируемый параметр; i = 1,….,m. Выражение (3. 5) исследуется на экстремум. Выражение для первой производной разрешается относительно искомого параметра g₁. Затем вторая и последующие системы подвергаются аналогичному преобразованию, в результате чего записывается набор уточненных значений параметров СЕ g_1, g₂…g_m, которые будут уточненными значениями элементов диагональной матрицы проводимостей. На основе уточненных данных строится уточненная диагностическая модель. Таким образом, использование метода постепенных приближений позволяет, не нарушая топологии ОД, расчетным способом определить параметры СЕ, точные данные по которым, как правило, отсутствуют. Для адаптации моделей электрических цепей средней и высокой размерности разработана программа ADAP 400.