Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования

Портнягин Н. Н., Пюкке Г. А.,

4.1. Построение априорной модели деградации системы на основе реализации марковского случайного процесса

Введем n – мерный вектор вероятностей состояний системы, 
P(j) = [P₁(j) P₂(j)……..P_n(j)], получаемый после j этапов воздействия матрицы  переходных вероятностей PP на вектор вероятностей начальных состояний системы: P(0) = [P₁(0) P₂(0)………P_n(0)]. Если s_k^j – случайное событие перехода системы после j этапов в k – e состояние (соответствующее появлению в системе дефектов или их отсутствию), то для каждого фиксированного j ≥ 1 имеет место полная группа событий: P_k(j) = 1, а коэффициенты матрицы РР = [P_mk^j] для однородного процесса будут характеризовать условную переходную вероятность P_mk^j = P[s_k^j | s_m^{j – 1}]. Для каждой строки матрицы РР имеет место соотношение

P_mk^j = P[s_k^j | s_m^{j – 1}] = 1.

Если принять потоки событий, переводящие систему из состояния в состояние, ординарными пуассоновскими, то матрица РР будет матрицей единичных скачков, а процесс, протекающий в системе, будет марковским процессом. Тогда текущий вектор вероятностей состояний системы будет определяться рекуррентным соотношением:

Р(j) = P(j – 1)*PP.

Процесс деградации при отсутствии восстановительных процедур будет сходиться к конечному состоянию максимально возможного количества отказов. Для упрощения процедуры аналитического описания процесса старения системы будем рассматривать простейший поток событий (стационарный, ординарный, с ограниченным последействием). Вместо плотности вероятности простейшего  потока f(t₁, t₂, …..,t_n) = f(t₁)f(t₂)……f(t_n),  одинаковой для всех интервалов времени между смежными событиями, ординарный случайный поток событий можно описывать числом отказов N(t), появляющихся на интервале времени от 0 до t. Для пуассоновского считающего стационарного процесса вероятность появления k событий в конечном интервале (0; t] определяется соотношением: p_k = P{N(t) = k}, k = 1, 2, ….. . Число событий в интервале (t₁, t₂] равно N(t₂) – N(t₁), счет начинается с нуля  p₀ (0) = 1.  Интенсивность потока отказов постоянна: λ = const, а число отказов на конечном интервале времени τ является дискретной случайной величиной k с законом распределения: p_k (τ) = [(λτ)^k / k!]exp(-λτ), где λτ – среднее число событий, приходящихся на участок τ. Вероятность отсутствия отказов на интервале τ распределена по закону p₀ (τ) = exp((-λτ),соответственно, закон распределения единичных отказов p₁(τ) = λτ exp((-λτ),двойных отказов p₂ (τ) =(( λτ)²⁄ 2!) exp((-λτ) и т. д. Необходимо отметить, что p_k (τ) = 1,  т. е. p_k (τ) образуют вероятностную весовую функцию для N(t). При одинаковых λ каждая из функций p_k(τ) имеет максимум при t_m = k/λ для k = 1, 2, …, и p_k (τ_m) =( k^ke^-k )/k! , т. е. положение максимума является линейной функцией от k , а значения p_k (τ_m) медленно убывают при возрастании k [1]. Если обозначить случайную величину Т₁ времени до появления первого дефекта (отказа первой компоненты разветвленной электрической цепи), то интегральная функция распределения для Т₁ будет иметь вид F(t) = 1 – exp(-λτ). Для пуассоновского процесса интервалы времени Т₁, Т₂ ....... между появлениями случайных отказов имеют общую интегральную функцию распределения и независимы. Если рассмотреть все возможные сочетания отказов, то на основе комбинаторных соотношений можно определить количество возможных состояний системы: С_m⁰ + C_m¹ + C_m² + ………+C_m^m = 2^m , где С_mⁿ = (1/n!)[m(m – 1)(m – 2) ……..(m – n+ 1) – количество сочетаний из m элементов по n; m – количество компонент схемы;  n = 1, 2, …., m. С_m⁰ – количество состояний отсутствия дефектов; C_m¹ – количество состояний одиночных дефектов; С_m² - количество состояний двойных дефектов; и т. д…. C_m^m – количество состояний m– кратных дефектов. Специфика задач диагностирования требует введения в множестве потенциально возможных состояний системы {S_i} совокупности подмножеств нулевых, одиночных, двойных и т. д. дефектов {S₀}; {S₁(1), S₁(2),……..,S₁(C_m¹)};  {S₂(1), S₂(2),…..., S₂(C_m²)};………..;{S_m-1(1), S_m-1(2),……….., S_m-1(C_m^m-1)}; {S_m}. Соответствующий граф состояний для простейшего потока событий должен быть преобразован в граф, включающий все обозначенные подсостояния, с учетом условия ординарности потока событий.  Квазидиагональная матрица единичных скачков по состояниям преобразуется в матрицу единичных скачков по подсостояниям. Для построения размеченного графа состояний системы необходимо проанализировать все разрешенные переходы системы из состояния в состояние на основе логического анализа процесса и условии ординарности потока событий. Процедура подсчета количества состояний по каждой совокупности сочетания дефектов легко формализуется на основе треугольника Паскаля:  При  вычислениях  необходимо  выбрать  строку,

.

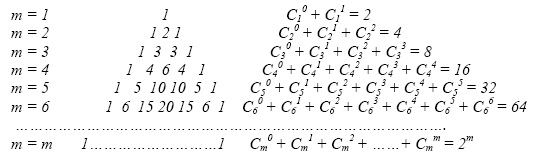соответствующую количеству m структурных единиц анализируемой схемы и выписать коэффициенты разложения строки, определяющие количество состояний системы по каждой совокупности сочетания дефектов. Построение графа состояний включает перечисление всех возможных сочетаний отказов S_i; i = 0, (2^m – 1) составляющих СЕ, установление всех разрешенных вероятностных переходов (на основе ординарности потока событий и отсутствии процедуры восстановления) и вычисления вероятностей этих переходов. При анализе цепей достаточно высокой размерности процедуру формирования графа состояний необходимо формализовать. Введем новую величину: характеристику текущего состояния α, представляющую собой дробь, в числитель которой будут входить индексы отказавших СЕ, а в знаменатель СЕ, сохранивших работоспособность. Обозначим характеристику начального состояния работоспособности всех m СЕ через α(0) = .

Алгоритм формирования множества возможных состояний системы начинается с α(0) и включает совокупность операций пошагового перемещения (инверсии) индексов из знаменателя в числитель с возвращением их в знаменатель на каждом очередном этапе инверсии. Алгоритм сходится к конечному состоянию неработоспособности всех СЕ с характеристикой α(2^m - 1) =. При машинной обработке данных, массив всех возможных состояний системы S(0); S(1); S(2)…………;S(2^m – 1) формируется на основе стандартной программы комбинаторного преобразования всех возможных сочетаний индексов 1, 2,…..,m из m элементов по i, где i = 1, m, кодирующих неработоспособные состояния системы. Результат заносится в таблицу характеристик текущего состояния (табл. 4. 1).Таблица имеет размер [max(C_m⁰ , C_m¹ , C_m² ,…….., C_m^m )](m+1).

После перечисления всех возможных состояний системы устанавливаются все разрешенные переходы. Критериями служат условия выполнения только одиночных перемещений индексов в выражениях характеристик текущего состояния системы, отсутствие процедуры восстановления и логический анализ процесса изменения работоспособности системы. При таких условиях все переходы будут носить однонаправленный характер (от состояний с меньшей кратностью дефектов к состояниям большей кратности). Скачки кратности дефектов на каждом переходе будут равны либо 1, либо 0 (0 – когда система остается в том же состоянии). Алгоритм вычисления разрешенных переходов выполняет сравнение характеристик предыдущих и последующих состояний, при этом каждая из характеристик подмножества k – кратных дефектов сравнивается со всеми характеристиками подмножества k + 1 – кратных дефектов (k = 0, 1, 2,……m – 1). Наличие разрешенного перехода определяется по отсутствию в знаменателе характеристики из подмножества (k + 1) – кратных дефектов совокупности цифр, принадлежащих числителю характеристики из подмножества k – кратных  дефектов.  В противном  случае  переход  не  устанавливается. Полученный граф будет иметь m + 1 подмножеств вершин, соответствующих дефектам различной кратности: S₀ – отсутствия дефектов; S₁ – одиночных дефектов; S₂ – двойных дефектов и т. д. S_m – mкратных дефектов.

Таблица 4.1. Характеристик текущего состояния системы

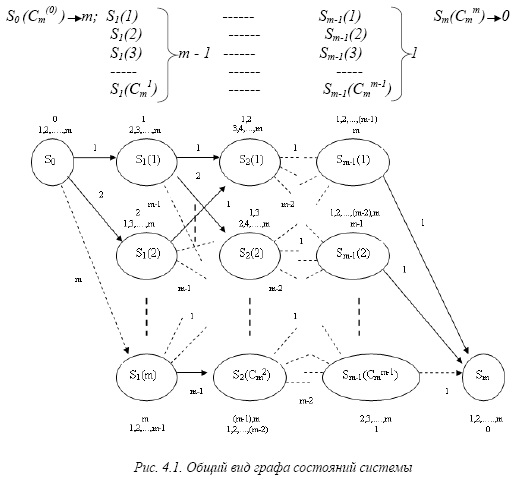
Количество разрешенных переходов, приходящихся на каждое состояние данной кратности будет убывать на единицу при переходе от подмножества кратности k к подмножеству кратности k + 1, где нижний индекс при S соответствует кратности дефекта, а индекс в скобках номеру состояния в подмножестве дефектов данной кратности. Величины (m, m-1,……, 2, 1, 0) – количества разрешенных переходов для каждого из состояний данной кратности. Общий вид графа предствлен на рис. 4.1.

.
 

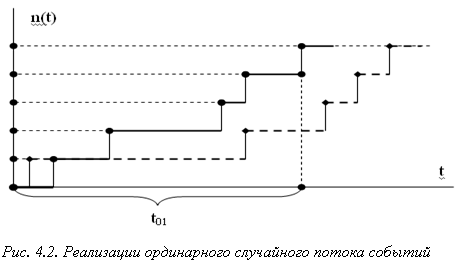
На основе полученного графа строится матрица вероятностей переходов РР. Теория надежности определяет время работы элемента системы до наступления отказа как случайную величину Т с распределением: F(t) = P{T ≤ t}, где Р – вероятность не возникновения отказа в течение заданного интервала времени (0, t]. Последнее выражение определяет область устойчивой работы элемента и позволяет определить только среднюю величину времени появления первого отказа, не указывая на характер самого процесса деградации свойств элементов. На рис. 4.2. изображены реализации n(t)ординарного случайного потока событий, где показана область устойчивой работы элемента (0, t₀₁]. Как было отмечено, при марковском подходе возможно рассмотрение постепенных отказов. При этом, согласно принятой методики, сначала кодируются последовательно все возможные состояния системы в порядке утраты ею функциональных свойств до состояния полного отказа. Далее строится граф состояний, на основе которого формируется матрица вероятностей переходов (в случае дискретного времени, или матрица интенсивностей переходов в случае непрерывного времени). Проводятся испытания по подтверждению гипотезы стационарности матрицы вероятностей переходов. Вычисление коэффициентов матрицы вероятностей переходов

. 

РР выполняется на основе заданной интенсивности отказов λ(t) = λ для стационарного процесса. Условная вероятность отказа в интервале (t, t + dt), при условии, что до момента t образец работал исправно определяется соотношением Р(В/A) = λdt , где А – событие: до момента t образец исправен; В – событие: образец отказал на интервале (t, t + dt). При пуассоновском потоке отказов функция распределения времени отказов, функция надежности и плотность распределения отказов будут определяться соотношениями: F(t) = 1 – e^-λt ; R(t) = e^-λt ; f(t) = λ e^-λt .

Основу методики прогнозирования технического состояния ОД будет составлять модель деградации, базирующаяся на процессе постепенного перераспределения численных значений компонент вектора первоначального распределения вероятностей состояний Р₀, при периодическом воздействии на вектор матрицы единичных переходов РР.

Таблица 4.2. Характеристик состояний трехкомпонентной системы

Однако такая априорная информация получена на основе статистических данных о значениях интенсивностей отказов компонент и для конкретного объекта исследования требует уточнения данных. Для этого необходимо выполнить адаптацию модели с целью повышения ее адекватности. Корректировку данных следует выполнять на основе опытных данных, полученных с ОД.

Например, для трехкомпонентной системы, имеющей 8 возможных состояний, в каждом из которых система может находиться с определенной вероятностью, распределение по подмножествам нулевых, одиночных, двойных и тройных дефектов составит: С₃⁰ = 1; С₃¹ = 3; С₃² = 3; С₃³ = 1.

Соответственно, характеристики текущего состояния системы распределятся по подмножествам k – кратных дефектов следующим образом 
(таблица 4.2).

На  основе  введенного  критерия  вычисления  разрешенных переходов строится граф состояний системы. Далее строится матрица вероятностей переходов РР. Наличие разрешенного перехода определяется по отсутствию в знаменателе  характеристики  из  подмножества (k + 1) – кратных дефектов совокупности цифр, принадлежащих числителю характеристики из подмножества k – кратных дефектов. 

.

Соответствующая стохастическая матрица переходов РР имеет вид:

.

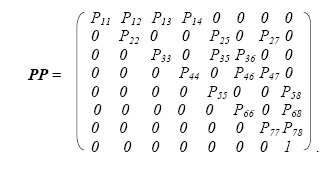 При заданных значениях времени наработки до отказа: t₁* = 10⁴ ч; t₂* = 1.25 • 10⁴ ч;   t₃* = 0.8 • 10⁴ ч.  Интенсивности  отказав  компонент  будут составлять λ₁ = 10^-4 ч^-1 ; λ₂ = 0.8 • 10^-4 ч^-1; λ₃ = 1.25 • 10^-4 ч^-1 . Соответственно, значения коэффициентов матрица РР при выбранном шаге дискретизации времени Δt = 10 ² ч, будут составлять:  

.
 

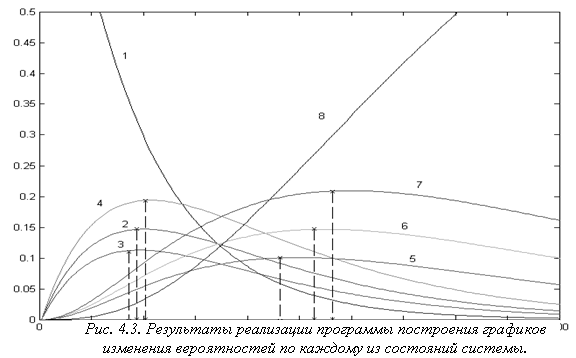
Процесс деградации при отсутствии восстановительных процедур будет определяться текущими значениями компонент вектора вероятностей состояний Р(j) = P(j – 1)*PP. Исходное состояние будет характеризоваться вектором P(0) = [1 0 0 0 0 0 0 0]. Машинная обработка данных в средеMATLAB при ручном формировании матрицы PP в командной строке дает возможность построить зависимости перераспределения изменения вероятностей по каждому из восьми состояний во времени. На рис. 4.3. приведена распечатка графиков изменения вероятностей отказов различной кратности во времени.

Кривая 1 интерпретирует изменение во времени вероятности работоспособного состояния ОД; кривые 2, 3, 4 - это зависимости изменения состояний одиночных отказов от времени; кривые 5, 6, 7 - это зависимости изменения состояний двойных отказов от времени. Следует отметить, что кривые, принадлежащие отказам одинаковой кратности сдвинуты во времени в силу различной интенсивности отказов у составляющих компонент. Группы кривых, принадлежащие различным кратностям отказов сдвинуты во времени в силу накопительного характера марковского процесса. 

Программа1 

.

Распределения вероятностей по состояниям работоспособности, одиночных и кратных дефектов могут быть получены с шагом дискретизации ?t = 10² ч после выполнения программы вычисления векторов промежуточных состояний системы. Текст программы с комментариями и результатами опробования приведен ниже.

.

Ниже приведены векторы сечения процесса в точках 37, 39, 42 и 98, 109, 119 итераций, соответствующих максимумам вероятностей одиночных и двойных отказов соответственно (максимумы выделены).

Необходимо отметить, что приведенная модель и примеры ее реализации отражают общие тенденции развития процесса деградации систем. Характер этих процессов полностью определяется величинами коэффициентов стохастической матрицы РР.

.

Для использования модели в качестве основы для разработки методики диагностирования необходимо наличие конкретной информации об объекте диагностирования. Поэтому полученную марковскую модель необходимо скорректировать. Далее рассматривается методика построения изоварной вероятностной модели и ее роль в процессе адаптации марковской модели деградации.