Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования

Портнягин Н. Н., Пюкке Г. А.,

1.3.3. Аналитические диагностические модели

Аналитическая модель ОД в общем случае может быть записана в виде:

Y = АX,

где X – вектор входных воздействий, Y – вектор реакций ОД, А – оператор преобразования.

Структура и параметры оператора А отражают показатели качества работы ОД. При этом задачи  проверки работоспособности и поиска дефектов решаются проверкой соответствия действительного оператора А заданному А₀ [71, 80].

Операторы А и А₀ должны определяться при фиксированном значении характеристик входных воздействий, т. е. в одном режиме работы ОД [33, 34, 81]. В частности, работоспособность ЭСА можно проверить по его реакции на единичную ступенчатую функцию т. е. по переходной характеристике [43, 78]. В работах [21, 43, 78, 111, 112] описываются методы и средства для контроля работоспособности ОД по показателям качества переходной характеристики.

Методы и устройства  получения частотных характеристик для решения задач диагностирования, применимые для ЭСА, описаны в работах [76, 77, 121, 126].

В случае невозможности организации требуемых режимов работы ОД, обойти эти трудности можно применением подхода, предусматривающего формулировку условий работоспособности непосредственно на множестве диагностических параметров [14, 83]. Эта задача может решаться методами теории чувствительности [44, 61, 125], методом малого параметра и другими.

Недостатком этого подхода является приближенное задание области работоспособности в виде прямоугольного параллелепипеда, что приводит к ошибкам контроля. Для перечисленных выше случаев проверки работоспособности необходима подача на ОД специального тестового воздействия [26, 27, 56, 62, 126].

При проверке работоспособности в процессе функционирования ОД можно использовать метод, заключающийся в сравнении выходных реакций ОД и его эталонной модели, включенной параллельно с ОД [72, 112, 113]. Достоинство этого метода состоит в том, что он позволяет решать задачу проверки работоспособности динамического звена, являющегося частью сложного ОД, при отсутствии доступа к входу и выходу этого звена [113].

Другой метод проверки работоспособности в процессе функционирования ОД состоит во введении избыточности в исходную систему [16]. Недостатком этих методов следует считать отсутствие информации о степени отклонения показателей качества переходного процесса, устойчивости ОД, поскольку применяется специальное задание условия работоспособности.

Поиск дефектов в ЭСА может строится в виде последовательности контрольных операций с определением параметров, характеризующих состояния отдельных блоков, элементов ЭСА и дальнейшем сравнением их с допустимыми значениями. При этом план поиска может основываться на известных статических характеристиках элементов ЭСА [56], на информационной оценке процесса диагностирования [70] или на основе анализа структурных особенностей ОД [29]. Недостатками этого метода являются неполнота диагноза, значительное суммарное время поиска за счет последовательной процедуры измерений, необходимость большого числа тестовых воздействий и разрыв связей между элементами.

Поиск дефектов в динамическом режиме позволяет осуществлять методы, использующие алгоритм распознавания образов [82]. При этом распознавание состояний ОД может  производиться либо в пространстве выходных сигналов ОД [124], либо в пространстве параметров модели ОД [82].

Для решения задачи методом распознавания образов необходимо определить совокупность диагностических параметров {ξ_j}; j = 1, …, k и построить образы отказавших блоков или СЕ, для которых требуется определить дефект. Для этого сначала формируется таблица неработоспособных состояний путем физического или математического моделирования с учетом заданной глубины поиска дефекта.

В диагностической модели могут использоваться дифференциальные и алгебраические уравнения. После введения дефекта в каждую СЕ, приводящего к ее отказу и отказу ОД измеряются значения параметров с помощью датчиков, установленных в соответствующих контрольных точках.

Результаты эксперимента сводятся в таблицу, число строк которой равно числу возможных дефектов в ОД S = {S_i}, где i = 1, …, n, а число столбцов множеству значений измеряемых параметров {ξ_j}. На пересечении i-го столбца и j-й строки записывается значение параметра ξ_ij при отказе i-й СЕ, т. е. состояния объекта S_i. Из рассматриваемой совокупности параметров {ξ_j} выделяют наиболее информативные, доступные измерению, однозначно соответствующие тому или иному отказу.

Совокупность диагностических параметров можно выбрать, воспользовавшись принципом разрешающей способности параметров:

ξ_j = {ξ_i  {ξ_j} / ¦ξ_ij – ξ_αj¦> ξ_пор^*},

где j = i, …, (n–1), α = (i + 1) … n, ξ_пор^* – значение порога чувствительности S_пор технического средства диагностирования.

Для выбранной совокупности диагностических параметров имеется ряд чисел ξ_ij^*. Совокупность этих чисел геометрически интерпретируют как точку в многомерном пространстве диагностических параметров. В результате в пространстве параметров появятся множества точек, характеризующих состояние ОД с соответствующими отказавшими СЕ. Распознавание дефекта в этом случае сводится к определению расстояния между точкой, соответствующей текущему состоянию ОД и всеми точками соответствующими неработоспособным состояниям. В результате процедуры распознавания осуществляется поиск дефекта СЕ, приведшему к отказу ОД [124].

Основным недостатком метода распознавания образов является недостаточно высокая гарантия выполнения однозначности идентификации дефекта в силу того, что области работоспособности могут оказаться довольно обширными, а вероятность наложение двух или нескольких областей может быть достаточно высока.

Существует метод поиска дефектов, основанный на анализе чувствительностей функций передачи к изменениям параметров СЕ объекта диагностирования. В реальном ОД величина функции передачи зависит от структуры ОД и величин параметров его СЕ. Все изменения, происходящие в ОД, приводят к изменению соответствующих функций передачи. В связи с этим различная чувствительность функций передачи находится как степень их изменения при варьировании какого-либо параметра.

Количественная оценка чувствительности дается через частные производные от функции передачи по изменяющемуся параметру:

S_ij = T_ij / r_α,

где T_ij – функция передачи от i-го полюса к j-му полюсу, r_α – изменяющиеся параметры.

Сравнивая чувствительности, можно упорядочить диагностические параметры по их влиянию на изменение состояния ОД, что составит алгоритм поиска дефекта. Обнаружить возникшие дефекты можно с помощью как рабочих, так и специальных тестовых сигналов.

Для поиска дефектов в линейных ОД используются методы, развитые в теории идентификации [101, 125]. Специфика диагностирования при этом заключается в том, что известными должны быть структурные и топологические особенности ОД, а определению подлежат только величины передаточных функций отдельных СЕ. Задача построения алгоритмов ПД при этом решается либо через определение коэффициентов передачи всего ОД с дальнейшей локализацией дефектов через известные уравнения связи между коэффициентами и параметрами отдельных СЕ [117], либо через непосредственное определение значений параметров, характеризующих техническое состояние отдельных СЕ с помощью алгоритмов идентификации. При определенной структуре ОД, его модели и известных номинальных значениях параметров его СЕ решение задачи ПД может быть сведено к решению обратной задачи теории чувствительности [101].

Недостатком первого подхода является необходимость решения системы нелинейных алгебраических уравнений относительно искомых параметров СЕ. При реализации второго метода возникают неудобства, заключающиеся в сложности получения функций чувствительности динамических характеристик к изменению параметров, характеризующих состояние ОД. Причем с увеличением глубины поиска дефекта или сложности структуры ОД эти неудобства возрастают. Тем не менее, применение теории чувствительности при разработке алгоритмов диагностирования принципиально позволяет едиными методами решать задачи проверки работоспособности [28], поиска дефектов [83] и выбора контрольных точек в ОД [72].

Поиск дефекта или определение состояния, в котором находится ОД, выполняется по алгоритму, включающему определенную совокупность проверок. Основополагающим принципом, которым руководствуются при построении алгоритма ПД, является принцип минимальных затрат – программных, временных и аппаратных.

Если не касаться методов индикации, то все возможные методы поиска дефектов в судовых ЭСА можно разделить на методы, алгоритм поиска дефекта которых основывается на известных статистических характеристиках элементов, и методы, основанные на данных анализа структуры ОД.

Наличие статистических данных позволяет построить алгоритм поиска по степени надежности контролируемых элементов, по максимальному получению информации для каждой последующей операции, а также на базе использования метода ветвей и границ. Анализ структуры ОД может быть выполнен на основе использования дифференциальных и алгебраических уравнений, описывающих ОД, передаточных функций контролируемой системы или методами инженерно-логического анализа [70].

Общим недостатком всех методов, построенных на использовании статистических данных, является то, что они учитывают не важность блоков и действительное состояние системы, а вероятностные величины, получаемые в результате анализа и обработки информации о подобных или сходных системах, т. е. статистические методы поиска, которые могут быть использованы только при наличии достоверных статистических данных [16].

Стремление повысить эксплуатационную надежность системы вызывает необходимость подвергать маршруты поиска непрерывной корректировке при изменении показателей системы, что несколько снижает ценность результатов, полученных таким путем. Поэтому необходимо разумно сочетать статистические вероятностные методы поиска дефекта с методами, основывающимися на анализе структуры системы, которые позволяют разделить систему на блоки или группы блоков и элементов.

К методам, основанным на анализе структуры системы с использованием статистических данных о безотказности элементов, относится метод, основанный на анализе функциональной модели. Анализ функциональной модели позволяет определить минимальную совокупность проверок {π_j}, которая обеспечит решение всех диагностических задач [79, 81, 84].

При поиске дефекта, как уже отмечалось ранее, составляют таблицу состояний на основе функциональной схемы, булеву матрицу, а затем определяют минимальное число проверок, выполнение которых позволит различить любое состояние [63, 81].

Полученные данные о структуре ОД могут быть использованы для решения задачи ПД методом ветвей и границ, базирующемся на анализе таблицы состояний и позволяющем получить программу поиска с минимальными затратами. При этом стоимость реализации заданной последовательности проверок Н определяется выражением:

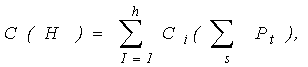
где С_i – стоимость i-й проверки, не зависящая от порядка выполнения проверок, Р_t – вероятность того, что система будет находиться в состоянии S_t, h– число внутренних вершин бинарного дерева H (π_k  S, V), соответствующего программе поиска, а S и V – соответственно количество висячих вершин и дуг в дереве.

Неопределенность в выборе первоначальной проверки позволяет расположить любую проверку π_l (l = 1, …, m) в корневой вершине и предположить, что поиск начинается именно с этой проверки. Проверка π_l разбивает множество состояний S на два непустых подмножества S_l⁰ и S₁¹, которые соответствуют двум возможным результатам проверки. Но т. к. последовательность выполнения последующих проверок неизвестна, то искомые решения заменяют их нижними границами СМ(S_l⁰) и СМ(S_l¹).

Стоимость поиска, начинающегося с выбранной проверки π_l, определяется соотношением:

CМ(π_l, S) = C_l 

где С_l – стоимость выполнения проверки π_l. Из множества m проверок выбирают ту проверку, для которой нижняя граница наименьшая. Затем определяют нижние границы для каждого из подмножеств S_l⁰ и S_l¹, выделенных на первом этапе:

СМ(π_f, S_l⁰) и СМ(π_g, S_l¹),

где π_f и π_g – фиксированные проверки на втором этапе. Средняя стоимость поиска при выбранных проверках на первом и втором этапах определяется соотношением:

Поступая в дальнейшем таким же образом, можно построить программу поиска в виде дерева решений.