Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Избранные работы по АСКУЭ (1981-2009)

Гуртовцев А. Л.,

Метрология цифровых измерений

Гуртовцев А.Л., к.т.н., ведущий научный сотрудник РУП "БЕЛТЭИ"

Дан критический анализ основных понятий метрологии измерительных систем (ИС) и их разновидности - автоматизированных систем учета и контроля электроэнергии (АСКУЭ). Выявлены недостатки исторически сложившихся методов метрологической аттестации современных цифровых ИС и АСКУЭ, предложены новые прогрессивные подходы в этой области метрологии. Показано, что в современных цифровых ИС и АСКУЭ процессы измерения функционально, конструктивно и территориально отделены от других процессов неизмерительного назначения - хранения, передачи и обработки измерительной информации, представленной в цифровом виде. Предложено выделять и метрологически аттестовывать в качестве средств измерений в ИС и АСКУЭ только их входную часть - первичные цифровые средства измерений, или измерительные каналы с цифровым выходом. Остальные системные средства необходимо рассматривать как вторичные средства неизмерительного назначения, требующие не метрологической, а цифровой аттестации. Новый подход позволяет существенно сократить затраты на метрологическое обеспечение ИС и АСКУЭ в процессе их разработки, внедрения и эксплуатации при одновременном сохранении всех требований обеспечения единства измерений. Рис.2, библ.39.

Предисловие

Причиной ревизии основных понятий метрологии измерительных систем (ИС) послужили современные цифровые автоматизированные системы учета и контроля электроэнергии (АСКУЭ) и работы автора в этом направлении [1-6]. В России в области метрологии электрических измерений существует большая нормативно-правовая и нормативно-техническая база, включающая в себя более двухсот документов различного уровня и назначения [7]. Тем не менее, как в России, так и в странах СНГ (включая Беларусь) отсутствуют прогрессивные метрологические документы (стандарты, методики, рекомендации, методические указания) на цифровые ИС и АСКУЭ. Более того, отсутствует даже среди специалистов четкое понимание того, что представляют собой цифровые ИС и чем они в метрологическом отношении принципиально отличаются от нецифровых систем.

Поэтому на цифровые ИС в странах СНГ (включая Россию) до сих пор автоматически распространяется действие метрологических документов, разработанных еще 20-30 лет назад для систем различного назначения (измерительных информационных, информационно-измерительных и измерительно-вычислительных комплексов), или новых документов, которые некритически, без учета достижений современных информационных технологий заимствовали устаревшие представления и положения прежней метрологии ИС. В частности, для России в настоящее время действуют в области ИС такие метрологические документы, как [8-23], для Украины - [8,10,24-28], для Беларуси - [8,10,24-37] .

ИС вчерашнего дня были ориентированы, как показано ниже, на технологии глобальной обработки измерительной информации в виде унифицированных аналоговых и дискретных сигналов. Современные же цифровые ИС и АСКУЭ используют в своей основе новейшие технологии обработки измерительной информации, представленной в виде рациональных чисел известной точности, с применением вычислительных машинных алгоритмов арифметики ограниченной точности. Например, в рамках цифровых АСКУЭ процессы аналоговых измерений сосредотачиваются только в ее входной части, на нижнем уровне - уровне масштабных преобразователей и электронных электросчетчиков с длительно хранимой в них базой данных учета, представленных в числовом виде, и с внешним доступом к этой базе по цифровым интерфейсам [5]. Аналогичные подходы внедряются сегодня и в другие цифровые ИС. Новые технологии построения цифровых ИС и АСКУЭ требуют пересмотра и переосмысления целого ряда метрологических понятий, сформировавшихся еще в эпоху аналоговых измерений и преобладающих в действующих метрологических документах.

В настоящей работе проводится ревизия таких базовых метрологических понятий, как измерение, средство измерений, измерительная система, измерительный канал и т.д. На основе критического анализа различных метрологических документов выявляется неудовлетворительное состояние ряда понятий и положений метрологии ИС: их неоднозначность, размытость, противоречивость. Становится очевидным, что существующие метрологические документы нельзя применять по отношению к цифровым ИС и АСКУЭ. Необходимо сформировать в метрологии, по крайней мере, относительно современных цифровых ИС, подвидом которых являются цифровые АСКУЭ, новый подход. Необходимо создать новое направление метрологии - метрологию цифровых измерений.

Часть 1

Критический анализ основных понятий метрологии

О понятии измерения

Согласно рекомендации РМГ 29-99 [10], метрология определяется как наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности». Именно поэтому ключевым понятием метрологии является измерение».

Одни и те же метрологические термины, приводимые в разных метрологических документах, имеют, как правило, различные определения, что затрудняет их согласованное понимание, порождает неопределенности или даже противоречия. Так, например, согласно [30] Измерение - совокупность операций, выполняемых для определения значения величины». Такая трактовка чрезвычайно широка, охватывая процессы, которые относятся не только к измерению, а в содержании понятия остаются неясными определяющие термины: о какой величине идет речь (физической, математической, психической и т.п.), какая совокупность операций относится к измерению, что должно являться значением величины (число, сигнал, код)?

В ГОСТе 16263-70, на смену которому пришли современные рекомендации РМГ 29-99, измерение определялось столь же расплывчато как "нахождение значения физической величины опытным путем с помощью специальных технических средств". Такая трактовка породила в 70-90-хх годах на страницах научных журналов ожесточенную полемику относительно того, как же надо понимать термин "измерение» и другие сопутствующие ему категории метрологии. Уже тогда многие авторы предостерегали от необоснованного расширения понятия измерения на любые операции приписывания чисел объектам материального мира (операции арифметизации), отмечая, что хотя измерение и сводится, в конце концов, к числовому представлению физических величин, но не всякое числовое представление этих величин есть измерение. Отмечалось, что …имеется озабоченность неопределенностью ряда понятий в метрологии и навязываемой "экспансией" метрологических терминов в другие сферы…из определения понятия "измерение" исчезла его сущность - сравнение измеряемой величины с другой величиной, принятой за единицу…имеется явная необходимость ограничить степень обобщения понятия "измерение" исходя из пользы научной и практической...».

Тогда же из-за отсутствия четкого определения и общепризнанного понимания термина "измерение", произошла путаница между близкими понятиями - "измерение", "контроль", "сравнение". Любое измерение есть процесс сравнения с единицей измерения, контроль может рассматриваться как частный случай измерения (когда не требуется знать конкретные значения физических величин, а только их отношения типа "больше", "меньше" или "равно"), но не каждая операция сравнения или контроля является операцией измерения. Поскольку границы распространения метрологии полностью зависят от того содержания, которое вкладывается в понятие измерение», постольку важно правильное его определение. Чрезмерное расширение этого понятия приводит к тому, что оно охватывает как измерения, так и вычисления, и под измерение попадают любые действия, связанные с приписыванием величине числа. Вместе с тем следует помнить, что метрология оперирует результатами, полученными экспериментально, т.е. путем измерений, а не вычислений. Поэтому процедуру по приписыванию числа величине без сопоставления ее с единицей измерения нельзя назвать измерением.

Рассмотренные замечания учтены в определении термина, данного в РМГ 29-99: Измерение физической величины - совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины». Здесь речь идет, во-первых, не о какой-то величине вообще, а о физической величине, во-вторых, о совокупности операций по применению особого технического средства, хранящего единицу физической величины, в-третьих, о совокупности операций, обеспечивающих нахождение соотношения измеряемой величины с ее единицей, в-четвертых, о получении значения этой величины. Важно примечание к этому определению в документе: "Приведенное определение понятия "измерение" удовлетворяет общему уравнению измерений, что имеет существенное значение в деле упорядочения системы понятий в метрологии. В нем учтена техническая сторона (совокупность операций), раскрыта метрологическая суть измерений (сравнение с единицей) и показан гносеологический аспект (получение значения величины)".

Отметим, что согласно РМГ 29-99, под значением физической величины подразумевается "выражение размера физической величины в виде некоторого числа принятых для нее единиц", а под ее числовым значением - "отвлеченное число, входящее в значение величины". Таким образом, результатом окончания процесса измерения должно быть определенное число, выражающее количество единиц измерения в измеряемой величине. Если говорить строго, то результатом измерения должно быть рациональное число, определенное с известной точностью. Вспомним, что целые и дробные числа (положительные, отрицательные и нуль) образуют множество рациональных чисел, которое замкнуто по отношению к арифметическим действиям, упорядочено в отношениях порядка больше» и меньше» и обладает свойством плотности, что и позволяет представлять при помощи этих чисел результаты измерений и вычислений с любой степенью точности.

В заключение отметим, что счет решает проблемы количественной идентификации множества дискретных объектов и их дискретных качеств, а измерение – количественной идентификации непрерывных (аналоговых) качеств этих объектов. В том случае, когда непрерывное качество физического объекта или процесса дискретизируется и результат такого аналого-цифрового преобразования (оцифровывания) может быть выражен совокупностью рациональных чисел известной точности, то процесс измерения можно считать оконченным. Последующие преобразования цифрового результата следует относить к процессу вычисления, а не измерения.

О результатах измерений. Прямые и косвенные измерения

Конечным результатом измерения физической величины должно стать определение ее значения, т.е. выражение размера физической величины в виде некоторого числа принятых для нее единиц. Размер физической величины – это ее количественная определенность, присущая конкретному материальному объекту, системе, явлению или процессу, а единица измерения физической величины - физическая величина фиксированного размера, которой условно присвоено числовое значение, равное единице, и применяемая для количественного выражения однородных с ней физических величин [10]. Размер физической величины имеет именование ее единицы измерения, а значение физической величины содержит как ее числовое значение (отвлеченное число), так и именование ее размера.

Согласно [10], результат измерения физической величины – значение величины, полученное путем ее измерения». Заметим, что именно путем измерения, т.е. экспериментально, а не путем вычислений вне средства измерений. Вместе с тем значения многих вторичных физических величин являются результатом вычислений над значениями первичных физических величин. В соответствии с этим метрология разделяет все измерения на прямые и косвенные. Согласно [10], прямое измерение - измерение, при котором искомое значение физической величины получают непосредственно» (уравнение измерения Q=q[Q], где Q- измеряемая величина, а q[Q] – результат измерения, причем q – числовое значение величины, а [Q]- ее размер). Важно примечание к данному определению: "термин прямое измерение возник как противоположный термину косвенное измерение. Строго говоря, измерение всегда прямое и рассматривается как сравнение величины с ее единицей (выделено автором)". Соответственно косвенное измерение - определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной» (уравнение измерения Q=f(X,Y,Z), где X, Y, Z - результаты прямых измерений, а Q – искомая величина).

При выполнении косвенных измерений необходимо в системе физических величин (согласно [10], система физических величин - совокупность физических величин, образованная в соответствии с принятыми принципами, когда одни величины принимают за независимые, а другие определяют как функции независимых величин) различать основные (основная физическая величина - физическая величина, входящая в систему величин и условно принятая в качестве независимой от других величин этой системы) и производные (производная физическая величина - физическая величина, входящая в систему величин и определяемая через основные величины этой системы) физические величины.

По линии глобального разделения всех измерений на прямые и косвенные (разновидностью косвенных измерений являются совокупные и совместные) проходит наиболее спорная область метрологии, вызывающая различное понимание того, что является измерением, а что им не является, где кончается измерение и начинается иной, неизмерительный процесс, что является средством измерения, а что им не является. Поскольку метрология должна обеспечить решение измерительных задач (согласно [10], измерительная задача - задача, заключающаяся в определении значения физической величины путем ее измерения с требуемой точностью в данных условиях измерений) для основных, или первичных (при прямых измерениях) и производных, или вторичных (при косвенных измерениях) физических величин, то следует определиться, в каких случаях вычисления (и другие операции не измерительного назначения) являются неразрывной составной частью процесса измерения, а в каких случаях их можно (и нужно!) отделить от процесса измерения и рассматривать автономно.

В документах действующей метрологии такая постановка вопроса до сих пор отсутствует [8-37]. Более того, под косвенные измерения и средства измерений, независимо от вида их реализации и свойств, до сих пор подгоняются все технические средства, в которых имеется хотя бы одна операция над результатом измерения, причем независимо от ее вида: хранение, передача, обработка, отображение, документирование и т.п.

О понятии средства измерений

Согласно РМГ 29-99, Средство измерений (СИ) - техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени». Важно примечание в документе к указанному определению: Приведенное определение вскрывает суть СИ, заключающуюся, во-первых, в "умении" хранить (или воспроизводить) единицу физической величины; во-вторых, в неизменности размера хранимой единицы. Эти важнейшие факторы и обуславливают возможность выполнения измерения (сопоставление с единицей), т.е. "делают" техническое средство средством измерения".

Корректное, т.е. в соответствии с их содержанием (сутью), применение на практике понятий измерение» и средство измерений», приведенных в РМГ 29-99, приводит к противоречиям со всеми другими метрологическими документами, в которых эти понятия некритично и необоснованно распространяется на все технические операции и средства, используемые совместно с истинными» СИ. Достаточно в качестве примера привести определение СИ из стандарта до сих пор действующего на территории стран СНГ (включая Россию) [8]: СИ - средство, предназначенное для измерений, вырабатывающее сигнал (показание), несущий информацию о значении измеряемой величины, или воспроизводящее величину заданного (известного) размера. СИ- это меры, компараторы, измерительные приборы, измерительные преобразователи, измерительные системы (выделено автором). Для СИ должны быть установлены МХ».

Примечательно, что в этом определении проявилась та устаревшая технология построения СИ, которая и позволила метрологам чрезвычайно расширить объем этого понятия в ущерб его содержанию: технология обработки сигналов (показаний). Об этом подробнее будет сказано ниже. По существу же во всех самых последних российских документах на ИС и АСКУЭ [12-23] проводится та же устаревшая метрологическая практика. Но ведь технологии-то с тех пор изменились, причем существенно!

 Об измерительной информации и первичных СИ

Числовое значение физической величины, о котором говорилось выше, не является единственным способом представления результата измерения. Более общий термин, отражающий как числовые значения физической величины, так и ее значения в иной форме (сигнала, отсчета, кода), – измерительная информация (согласно [10] определяется как информация о значениях физических величин»). Отметим противоречивость понятий значение физической величины» и измерительная информация»: в первом значение физической величины выражается в виде некоторого числа принятых для нее единиц, а во втором подразумевается, что значения физических величин могут отличаться от числового (в противном случае, если нет отличий, то нет и смысла вводить термин измерительная информация» дополнительно к термину значение физической величины»).

Разновидностью измерительной информации является сигнал и отсчет. Согласно [10], измерительный сигнал - сигнал, содержащий количественную информацию об измеряемой физической величине, а отсчет показаний средства измерений - фиксация значения величины или числа по показывающему устройству средства измерений в заданный момент времени. Помимо представления значения физической величины в виде числа (подразумевается рациональное число ограниченной точности), сигнала и нецифрового отсчета – регламентированных видах измерительной информации, возможно ее представление и в виде некоего кода (двоичного, шестнадцатеричного, двоично-десятичного и др.). Но в РМГ29-99 определение такого способа представления измерительной информации отсутствует.

То, что в большинстве СИ (в частности, в ИС) до сих пор результат измерения представляется не в виде числа, а в виде сигнала, отсчета или кода, является одной из причин того, что любые операции над данными видами измерительной информации трактуются как измерительные, а технические средства, в которых реализуются эти операции, определяются как СИ. Имеются и другие причины такого положения, о которых будет сказано ниже.

Прежде, чем перейти к анализу особенностей ИС, рассмотрим кратко первичные СИ, к которым относят меры, измерительные устройства, измерительные приборы, измерительные преобразователи, датчики и измерительные установки. Согласно [10], мера физической величины - СИ, предназначенное для воспроизведения и (или) хранения физической величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью, а измерительный прибор - СИ, предназначенное для получения значений измеряемой физической величины в установленном диапазоне.

Согласно [10], измерительный преобразователь (ИП) - техническое средство с нормативными метрологическими характеристиками, служащее для преобразования измеряемой величины в другую величину или измерительный сигнал, удобный для обработки, хранения, дальнейших преобразований, индикации или передачи. Важно примечание к данному определению: "По характеру преобразования различают аналоговые, цифро-аналоговые, аналого-цифровые преобразователи. По месту в измерительной цепи различают первичные и промежуточные преобразователи. Выделяют также масштабные и передающие преобразователи". Аналогично, первичный измерительный преобразователь (ПИП) - ИП, на который непосредственно воздействует измеряемая физическая величина, т.е. первый преобразователь в измерительной цепи измерительного прибора (установки, системы), а датчик - конструктивно обособленный первичный преобразователь, от которого поступают измерительные сигналы (он "дает" информацию). Важно примечание: "Датчик может быть вынесен на значительное расстояние от СИ, принимающего его сигналы".

Согласно [10], измерительное устройство - часть измерительного прибора (установки или системы), связанная с измерительным сигналом и имеющая обособленную конструкцию и назначение, измерительная цепь - совокупность элементов СИ, образующих непрерывный путь прохождения измерительного сигнала одной физической величины от входа до выхода, а измерительная установка - совокупность функционально объединенных мер, измерительных преобразователей и других устройств, предназначенная для измерений одной или нескольких физических величин и расположенная в одном месте.

Заметим, что в вышеприведенных определениях первичных СИ форма представления измерительной информации либо не указывается (полагается, что она не имеет значения, хотя это и не так, как показано ниже), либо определяется как измерительный сигнал (для преобразователей, датчиков, измерительных устройств и цепей). Перейдем к анализу ИС, которые являются основным предметом данной работы.

О понятии измерительных систем

Согласно [10], измерительная система (ИС) - совокупность функционально объединенных мер, измерительных приборов, измерительных преобразователей, ЭВМ и других технических средств, размещенных в разных точках контролируемого объекта и т.п. с целью измерений одной или нескольких физических величин, свойственных этому объекту, и выработки измерительных сигналов в разных целях. Важно примечание к определению: "В зависимости от назначения измерительные системы разделяют на измерительные информационные, измерительные контролирующие, измерительные управляющие системы и др.".

Обратим внимание на то, что в определении ИС превалирует как результат измерения измерительный сигнал, а не числовое значение величины: …с целью измерений…и выработки измерительных сигналов…». Кроме того, в самом определении ИС не делается различий между СИ (мерами, измерительными приборами, измерительными преобразователями) и другими техническими средствами, включая ЭВМ, по существу, неизмерительного назначения. Полагается, что все эти средства применяются с целью измерения».

Аналогичные, только более детальные определения ИС, приведены в документе СНГ [26] и российском стандарте [9]:

ИС- техническое устройство, предназначенное для измерений и представляющее собой, в общем случае, совокупность измерительных приборов, измерительных преобразователей (в том числе, устройства согласования сигналов), мер, измерительных коммутаторов, линий связи, цифровых и аналоговых вычислительных устройств, объединенных общим алгоритмом функционирования и предназначенных для автоматического (автоматизированного) получения данных о состоянии объекта путем измерительных преобразований множества изменяющихся во времени и распределенных в пространстве величин, характеризующих это состояние; машинной обработки результатов измерений; регистрации и индикации результатов измерений и результатов их машинной обработки; преобразования этих данных в выходные сигналы системы»;

"ИС - совокупность измерительных, связующих, вычислительных компонентов, образующих измерительные каналы (ИК), и вспомогательных устройств (компонентов измерительных систем), функционирующих как единое целое, предназначенная для: получения информации о состоянии объекта с помощью измерительных преобразований в общем случае множества изменяющихся во времени и распределенных в пространстве величин, характеризующих это состояние; машинной обработки результатов измерений; регистрации и индикации результатов измерений и результатов их машинной обработки; преобразования этих данных в выходные сигналы системы в разных целях".

Эти определения, при общем сходстве с предыдущим, отличаются от него наличием большего количества компонентов, характеризующих внутреннее устройство (структуру) системы, а также большим перечнем выполняемых системой функций.

Характерными свойствами ИС является размещение технических средств в разных точках контролируемого объекта и т.п.» (первое определение) и получения данных о состоянии объекта путем измерительных преобразований множества изменяющихся во времени и распределенных в пространстве величин» (второе определение). Таким образом, из сути двух определений ИС следует важный вывод – различные технические средства ИС размещаются в разных точках пространства и используются для измерения физических величин, изменяющихся во времени и распределенных в пространстве. Как следствие, процесс измерения с использованием пространственно распределенных различных, обособленных в функциональном и конструктивном исполнении технических средств ИС, порождает пространственное и временное распределение исходной, промежуточной и результирующей измерительной информации (в форме чисел, отсчетов, сигналов, кодов). Для интеграции такой распределенной во времени и в пространстве информации необходимо обеспечить соответствующие условия ее хранения, передачи, обработки, отображения, регистрации, документирования и дальнейшего использования.

На рис.1 приведена типовая структурная схема ИС, содержащая датчики, измерительные преобразователи (одноканальные и многоканальные), коммутаторы, аналого-цифровые преобразователи (АЦП) и цифровой вычислительный компонент (ЦВК) [26]. Из схемы ясно, что большая часть ИС (ее первичная и вторичные части) осуществляет аналоговые преобразования измерительных сигналов, и только на выходе вторичной части (на выходе АЦП) появляются промежуточные значения физических величин, представляемые в виде цифрового кода (не чисел!). Получение числовых результатов измерений происходит только в конечном компоненте ИС – в ЦВК в процессе приема им в реальном масштабе времени кодов с АЦП и их последующей дискретной обработки (вычислений) в своей разрядной сетке (с достаточной разрядностью для достижения требуемой точности вычислений) с использованием соответствующих форматов данных и алгоритмов.

Рассмотренная структура ИС типична и является предметом не только одного метрологического документа [26], но и многих других (например, [29]). Такие ИС по своей метрологической сути идентичны первичному СИ, выполненному в виде конструктивно и функционально законченного технического изделия: измерительного прибора, измерительного преобразователя или датчика. Внутри такого технического средства могут выполняться различные операции, причем как измерительного, так и неизмерительного назначения, но в целом это средство должно рассматриваться как СИ.

Отметим, что рассмотренные системы, независимо от их назначения и состава оборудования, трактуются по существу как сильносвязанные системы, или как единые СИ. Такой подход к ИС, имеющий исторический характер, основан на преобладании в большинстве системах аналоговых и дискретных преобразований, но в силу же историчности начинает себя изживать. Уже появились и начинают широко распространяться ИС с преобладанием цифровых преобразований и числового представления измерительной информации (например, цифровые АСКУЭ). Новые цифровые технологии и ИС, построенные на их базе, требуют пересмотра ряда понятий традиционной метрологии, сложившейся в тысячелетнем процессе развития аналоговых измерений.

В рассматриваемой структуре ИС преобразования измерительной информации распределены пространственно между компонентами системы, но жестко связаны во времени: информация на выходе одного компонента должна в реальном времени, с минимальными задержками быть обработана следующим в измерительной цепи компонентом. Длительное хранение информации, представленной в аналоговом или дискретном виде в том или ином компоненте ИС (за исключением ЦВК), невозможно и недопустимо. Такую структуру системы можно назвать слабосвязанной в пространстве (компоненты конструктивно и пространственно обособлены друг от друга), но сильносвязанной во времени (связь во времени между функционирующими компонентами нельзя прервать даже на короткий период). В этой ИС все операции, производимые теми или иными компонентами, независимо от их вида (измерительные, связующие, вычислительные), являются составной частью процесса измерения и не могут быть из него вычленены. Неправильная работа какого-либо компонента, даже такого пассивного, как линия связи, автоматически приведет к ошибочному результату, т.е. к метрологическому отказу.

В итоге, хотя ИС содержит пространственно, конструктивно и функционально обособленные компоненты различного назначения, система в целом должна рассматриваться как единое, целое СИ, с вытекающими из этого признания соответствующими метрологическими последствиями: утверждением или аттестацией типа СИ и его метрологическим контролем. Такая ИС по своей метрологической сути идентична первичному СИ, выполненному в виде законченного изделия (измерительного прибора, измерительного преобразователя или датчика). Внутри такой системы могут выполняться различные операции, как измерительного, так и неизмерительного назначения, но в целом она должна рассматриваться как СИ. Основой реализации всех подобных систем является технология глобальной обработки измерительной информации в виде унифицированных аналоговых или дискретных сигналов. Поэтому такие ИС можно с полным основанием назвать нецифровыми (в них цифровой результат формируется не внутри системы, а только на ее выходе).

Совсем иная картина складывается в случае цифровых ИС, типичным представителем которых являются цифровые АСКУЭ. Современные цифровые ИС и АСКУЭ используют в своей основе новейшие технологии глобальной машинной обработки измерительной информации, представленной в цифровом виде. В частности, в рамках цифровой АСКУЭ процессы аналоговых измерений сосредотачиваются только в ее входной части, на нижнем уровне - уровне масштабных преобразователей (измерительных трансформаторов тока и напряжения) и электронных электросчетчиков с длительно хранимой в них базой измерительных данных, представленных в числовом виде, и с внешним доступом к этой базе через цифровые интерфейсы по различным каналам связи. Все иные процессы на других уровнях цифровой системы представляют собой исключительно процессы неизмерительного назначения – процессы передачи, хранения, обработки, анализа, отображения, документирования и распространения цифровой информации известной точности (точность представления и обработки такой информации на порядки выше точности результатов измерений, представленных в цифровом виде внутри системы на ее нижних уровнях). Эти процессы не относятся к процессам измерений, а только используют их результаты.

Принципы создания цифровых АСКУЭ широко распространяются сегодня и в других цифровых ИС, использующих на нижнем уровне первичные измерительные преобразователи с цифровым выходом и длительно хранимой цифровой базой данных, формируемой в точке измерения. Результатом применения таких технологий является то, что ИС становятся слабосвязанными системами не только в пространстве, но и во времени: доступ к цифровым измерительным данным нижнего уровня систем возможен практически в любое время при полной гарантии сохранения результатов измерений в точке измерения и их неискаженного получения для дальнейшей обработки на верхних уровнях системы. Новые технологии построения цифровых ИС и АСКУЭ требуют пересмотра и переосмысления целого ряда метрологических понятий, сформировавшихся в эпоху аналоговых измерений и преобладающих до сих пор в действующих метрологических документах.

 О понятии измерительного канала

Предшественник понятия измерительного канала - понятие измерительной цепи. Согласно [10], измерительная цепь - совокупность элементов средств измерений, образующих непрерывный путь прохождения измерительного сигнала одной физической величины от входа до выхода. Для измерительных систем измерительная цепь превращается в измерительный канал (ИК).

Согласно [30], ИК системы - функционально объединенная совокупность технических средств, предусмотренная алгоритмом его функционирования, выполняющая законченную функцию от восприятия измеряемой величины до индикации или регистрации результата измерения включительно, или преобразование результата измерения в сигнал, удобный либо для дальнейшего использования вне ИС, либо для ввода в цифровое или аналоговое устройство, входящее в состав ИС. Согласно [26], ИК ИС - последовательное соединение измерительных каналов измерительных компонентов ИС, предусмотренное алгоритмом ее функционирования, выполняющее законченную функцию от восприятия измеряемой величины до индикации или регистрации результата измерения включительно, или преобразование его в сигнал, удобный либо для дальнейшего использования вне ИС, либо для ввода в цифровое или аналоговое вычислительное устройство, входящее в состав ИС. Идентичное определение дано в [28].

В других документах [24,27,31,33,34] определения ИК существенно отличаются друг от друга. Общее в них только то, что ИК представляет собой цепь последовательно соединенных технических средств, образующих непрерывный путь прохождения измерительной информации от ее входа до выхода и предназначенных для измерения одной физической величины. Расхождения начинаются далее по использованию ИК, по его структуре, по виду измерительной информации в ИК, по трактовке того, где и чем оканчивается ИК. Так, в одних определениях ИК понимаются по использованию как часть ИС, а в других – как отдельные, самостоятельные средства. По структуре ИК в одних определениях все технические средства ИК представляются как СИ, в других как СИ - другие технические средства, в-третьих – как комплекс измерительных преобразователей (СИ конкретного вида), в-четвертых – просто как функционально объединенная совокупность технических средств. Под измерительной информацией, проходящей через ИК, большинство определений понимают измерительный сигнал (аналоговый). По месту и виду окончания ИК также существует разноголосица: в одних случаях ИК выполняет законченную функцию от восприятия измеряемой величины до ее индикации или регистрации результата измерения включительно (не уточняется в каком виде), в других - до преобразования результата измерений в сигнал, удобный для использования вне ИС, в третьих - до преобразования результата измерений в сигнал, удобный для ввода в цифровое или аналоговое устройство, входящее в состав ИС, в четвертых – вообще отсутствует указание на то, где и чем кончается процесс измерения физической величины в ИК.

Такие размытые, не согласованные друг с другом определения ИК, приведенные в различных метрологических документах, ничего кроме путаницы вызвать не могут.

Часть 2

Метрология цифровых измерений

К метрологии цифровых измерений

В предыдущей части настоящей работы показано, что основные понятия метрологии были сформированы в прошлом применительно к технологиям, основанным на аналоговых и дискретных измерениях с представлением результатов измерений, как правило, в форме аналогового сигнала, стрелочного отсчета или кода, и в последнюю очередь в числовом виде. При этом любая ИС, содержащая различные компоненты как измерительного, так и неизмерительного назначения, автоматически рассматривается как СИ, подлежащее метрологической аттестации и поверке, причем как в целом, так и покомпонентно. Более того, в условиях российской метрологии каждая такая система должна утверждаться как единичный тип СИ с обязательным внесением ее в Государственный реестр СИ [9]. Такой подход был оправдан для технологии аналоговых и дискретных измерений, но становится тормозом для развития технологии цифровых измерений.

Исходным моментом в появлении цифровых технологий измерений следует признать 1971 год, когда был создан первый микропроцессор. Но прошло более двадцати лет, прежде чем микропроцессоры в ходе своей эволюции получили массовое внедрение в различных СИ. В области измерения и учета электроэнергии электронные микропроцессорные электросчетчики стали широко распространяться в мире в начале 90-х годов. В микропроцессорных СИ прямые измерения составляют лишь незначительную часть всего процесса нахождения значения измеряемой физической величины, второй и главной частью которого являются операции хранения, передачи и обработки результатов прямых измерений, представленных в числовом (в цифровом) виде. Такие операции до сих пор рассматриваются традиционной метрологией как косвенные измерения, хотя по существу к процессу измерения уже никакого отношения не имеют.

Когда измерительные, вычислительные и иные операции реализуются в рамках конструктивно и функционально законченного СИ (датчика, измерительного преобразователя, измерительного прибора), то отделить с метрологических позиций измерительные операции от вычислительных операций не представляется возможным - на выходе СИ имеется числовой результат, и внутренние операции его получения метролога не интересуют. Важна лишь точность и достоверность этого результата, которая обеспечивается метрологической аттестацией СИ.

Ситуация меняется, когда в рамках сложных ИС используются конструктивно и функционально (а часто и территориально удаленные) обособленные компоненты, часть из которых реализует прямые измерения с представлением их результатов в числовом виде, а другая часть – числовую обработку этих результатов. Относить в этих новых цифровых системах все компоненты (в том числе неизмерительные компоненты: цифровой вычислитель, цифровую память, программное обеспечение, цифровой канал связи, модем, монитор, принтер и т.п.) к СИ нет разумных оснований. В цифровых ИС следует с метрологических позиций отделить измерительные компоненты от всех иных, рассматривать первые компоненты как СИ, а все остальные технические средства – как специализированные или универсальные средства неизмерительного назначения. Соответственно нельзя, если строго следовать понятию измерения, рассматривать как СИ и ИС в целом. Необходимо, наконец, назвать вещи своими именами: измерение - измерением, а вычисление - вычислением.

Возникает простой вопрос: поскольку конечный результат на выходе цифровой ИС формируется в двух различных, но взаимосвязанных процессах – процессе измерения, который имеет нормируемые метрологические характеристики, и процессе вычисления, который, по всей видимости, не должен иметь таких характеристик (поскольку не является процессом измерения), то каким же образом будет обеспечена точность и достоверность конечного результата? Очевидно, что для достижения этого необходимо к средствам неизмерительного назначения предъявить определенные требования по точности выполнения ими операций, связанных с преобразованием чисел (операций хранения, передачи, обработки, отображения и документирования). Эта точность должна быть такова, чтобы ее вклад в понижение точности результатов измерений, полученных в числовом виде на выходе СИ, входящих в состав цифровой ИС, был пренебрежимо мал.

Казалось бы, заменяя метрологические требования к техническим средствам неизмерительного назначения вычислительными требованиями по точности, ничего нового мы не получаем? В чем же разница, в чем выигрыш? А разница в том же, в чем разница между измерением и вычислением. Первое представляет собой сложный процесс аналогового сравнения измеряемой величины с единицей измерения, второе – элементарные арифметические действия над рациональными числами. Для повышения точности аналоговых операций необходимы серьезные технологические достижения, а для повышения точности числовых операций достаточно всего лишь увеличить разрядность чисел. Например, для двоичных чисел, в случае представления их в формате с плавающей запятой, дополнительный двоичный разряд мантиссы дает возможность увеличить точность представления двоичного числа в 2 раза, а дополнительный байт (8 двоичных разрядов) - в 28= 256 раз. Такие темпы повышения точности недостижимы для аналоговых измерений. Если относительная погрешность аналоговых измерений составляет 0,1% (очень высокая точность, например, при измерении количества электроэнергии), то для вычислителя, на вход которого поступают числа такой точности, без особых проблем можно обеспечить точность их промежуточного представления и обработки в 100 раз выше, и для этого потребуется всего лишь двухбайтная мантисса. На выходе вычислителя, округлив результат до точности исходных чисел, мы можем быть уверены, что подпортили» их точность не более чем на одну сотую часть.

Так почему же необходимо принять новый, психологически непривычный для метрологов подход к цифровым ИС? Во-первых, потому, что он имеет разумные основания и устраняет из метрологии путаницу, связанную с понятиями прямых и косвенных измерений (такие средства, как цифровой вычислитель, модем, монитор, принтер и т.п. не могут быть отнесены к средствам измерения при всем желании метрологов). Во-вторых, потому, что метрология освобождается от излишней нагрузки: от тех применений, в которых она принципиально не может создать эффективных решений, а лишь демонстрирует некую видимость обеспечения единства измерений. Тем самым метрология сможет продуктивнее развиваться именно в тех направлениях, которые ей изначально свойственны: в области эталонов, мер и аналого-дискретных измерений. В-третьих, потому, что цифровой подход существенно снижает людские, материальные, финансовые и временные затраты на создание массовых цифровых ИС, поскольку не требует утверждать единичный тип ИС в качестве СИ или производить их метрологическую аттестацию и многочисленные поверки.

Прежде, чем ниже будут сформулированы основные понятия метрологии цифровых измерений, или цифровой метрологии, изложим кратко основы представления рациональных чисел, их арифметической обработки и достижения требуемой вычислительной (не метрологической!) точности.

Машинное представление чисел и их арифметическая обработка

Для понимания особенностей обработки рациональных чисел, которые, в частности, должны быть результатом измерений, рассмотрим основные способы их представления в технических системах (машинного представления) и арифметической обработки, являющейся основой машинных вычислений любых видов и сложности [38].

Изображение чисел в любой позиционной системе счисления с натуральным основанием R (R>1) базируется на представлении их в виде произведения целочисленной степени Rm основания R на полином от этого основания:

AR= ±Rm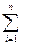aiR-i (1)

где ai Є (0,1,…,R-1) – цифры R-ичной системы счисления (R-ичные цифры); n – количество разрядов (разрядность), используемых для представления числа; Rm – характеристика числа, причем показатель m Є (…, -2, -1,0,+1,+2,…); RmR-I = Rm-i – позиционный вес i-го разряда. В десятичной (R=10) системе счисления для представления чисел используются цифры ai= (0,1,…,9), в двоичной (R=2) - ai= (0,1), в шестнадцатиричной (R=16) - ai= (0,1,…,9, A,B,C,D,E,F), где прописным латинским буквам A,B,C,D,E,F соответствуют числа 10,11,12,13,14,15.

Если m=const, то (1) определяет представление числа в форме с фиксированной запятой (фиксированной точкой). Позиция, в которой запятая фиксируется между разрядами числа, отделяет целую часть от дробной и, определяя вес соответствующих разрядов, постоянна в процессе вычислений для всего множества используемых рациональных чисел и зависит только от установленного значения m. Если m≤0, то формула представляет дробные числа (правильные дроби), если m≥n – целые числа, если 0<m<n – смешанные числа (неправильные дроби). Обычно для чисел с фиксированной запятой значение m ограничено 0≤m≤n, т.е. позиция запятой в числе выбирается в рамках n разрядов, отведенных для изображения цифровой части числа.

В микропроцессорах основой представления чисел является двоичная система счисления. В двоичной системе счисления при R=2 и m=0 формула представления дробных двоичных чисел имеет вид

A2= ±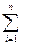ai2-i =±,а1а2…аn (2)

где 2-i – вес i-го двоичного разряда. Формула (2) определяет дробные двоичные числа со знаком. Левая ее часть дает развернутую форму записи числа в виде полинома, а правая – свернутую форму записи в виде последовательности цифр (коэффициентов полинома). Для отображения знака числа отводится дополнительные знаковый разряд (нулевой с весом 20), а запятая фиксируется перед старшим (с весом 2-1) цифровым разрядом числа. Если заранее известно, что множество используемых чисел не содержит отрицательных чисел, то в формате числа знак можно опустить. Такие числа называют беззнаковыми. В n-разрядной сетке дробных беззнаковых чисел может быть точно представлено 2n различных, в том числе 2n-1 ненулевых чисел, удовлетворяющих неравенству

A2min=2-n≤A2≤A2 max =1-2-n (3)

где A2min – минимальное (не нулевое), A2 max – максимальное из представимых чисел.

В случае R=2 и m=n формула (1) преобразуется к виду:

A2= ±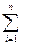ai2n-i = ±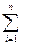bi2i = ±bn-1…b1b0 (4)

где bi= an-1. Перекодировка индексов в формуле (4) дает удобочитаемое соответствие веса разряда 2i индексу его цифры. Данная формула определяет целые двоичные число со знаком. Под знак отводится дополнительный (n+1-ый разряд с весом 2n, а запятая фиксируется после младшего (нулевого с весом 20) цифрового разряда числа. Для беззнаковых целых чисел знак опускается. В n-разрядной сетке целых беззнаковых чисел может быть представлено множество 2n целых, в том числе 2n-1 ненулевых чисел, удовлетворяющих неравенству:

A2min=20=1≤A2≤A2 max =2n-1 (5)

В свернутой форме эти числа изображаются такими же последовательностями цифр, как и дробные числа, отличаясь лишь положением запятой: A2min=00…01, A2max=11…11.

В формулах (2) – (5) двоичные числа представлены в виде полиномов, коэффициенты которого выражены двоичными цифрами, а основание – десятичным число, т.е. цифрой 2. Учитывая, что в любой позиционной системе счисления ее основание однозначно представляется с помощью цифр этой системы в виде 10R (по определению R=(R-1)+1, а такая операция дает нуль в младшем разряде и единицу переноса в старший разряд), формулы можно обобщить на случай любой позиционной системы (соответственно для дробных и целых чисел):

AR= ±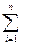ai10R-i , AR min =10R-n≤|AR|≤AR max =1-10R-n (6)

AR= ±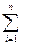ai10Ri , AR min =1≤|AR|≤ AR max =10Rn – 1 (7)

В формулах (6), (7) обозначение модуля введено для знаковых чисел, а неравенства справедливы для всех ненулевых значений чисел. Эти формулы полезны при рассмотрении чисел в десятичной и шестнадцатеричной системах счисления, которые широко используются в микропроцессорах наряду с двоичной системой. В системах с R=10 или R=16 используются смешанные системы счисления, в которых каждая цифра R-ичной системы изображается цифрами другой, Q-ичной (Q<R), в частности, двоичной системы.

В микропроцессорах, как и в любых других технических средствах, выполняющих автоматические вычисления, количество разрядов n, отводимых для представления чисел, ограничено и фиксировано как для базовой сетки микропроцессора (его технической разрядности), так и для конкретных программ, которые могут использовать разрядность данных, кратную базовой. Этот факт, наряду с использованием для представления чисел двоичной системы, приводит к существенным отличиям машинной арифметики от обычной абстрактной арифметики, реализуемой посредством неограниченных абстрактных ресурсов (мозга, бумаги и карандаша). Назовем числа, представляемые в фиксированной разрядной сетке, числами с ограниченной точностью, а машинную арифметику – арифметикой ограниченной точности (АОТ).

Рассмотрим основные свойства АОТ. Как следует из формул (6), (7), числа |AR|<ARmin и |AR|>ARmax нельзя представить в n-разрядном формате, поскольку представимые числа принадлежат диапазону {(-ARmax, -ARmin, ), 0, (+ARmin , +ARmax)}. Если при выполнении арифметических операций появляется число |AR|>ARmax, то это приводит к переполнению n-разрядного формата числа и, как правило, ошибочному представлению результата операции (ошибка переполнения). Наоборот, если при выполнении операции возникает такое ненулевое число, что AR|<ARmin, это приводит к антипереполнению формата (потере значности), при котором ненулевые числа приходится представлять в виде нуля (машинного нуля).

Появление ошибок переполнения и машинного нуля в АОТ нарушает ряд аксиом, истинных в арифметике точных чисел, в частности, ассоциативный а+(в-с)=(а+в)-с и дистрибутивный а∙(b-с)=a∙b-а·с законы. В АОТ порядок операций, позволяющий избежать ошибок переполнения и машинного нуля, имеет важное значение для получения правильного результата вычислений. Выявление ошибок переполнения и антипереполнения является задачей, которую необходимо решать при разработке арифметических программ.

Диапазон (ARmin , ARmax) точного представления в АОТ ненулевых дробных R-ичных чисел имеет дискретный характер, т.е. в пределах этого диапазона точно представляется лишь то множество чисел, в записи которых отличные от нуля цифры содержатся только в первых n после запятой разрядах (остальные дополнительные разряды, если предположить их существование, будут содержать нули). На практике приходится представлять в n-разрядном формате любые дробные числа из указанного диапазона, в том числе и те, разряды которых, выходящие за рамки принятого формата, содержат ненулевые цифры (см. понятие плотности рациональных чисел в части 1). Например, десятичная дробь 0,1 в двоичном формате представляется бесконечной периодической двоичной дробью 0,0(0011). При записи этой дроби в ограниченном формате приходится отбрасывать ряд ненулевых цифр, находящихся за пределами первых n двоичных разрядов, и тем самым представлять ее как приближенное число с ограниченной точностью.

Числа с ограниченной точностью порождаются не только в процессе их начального представления в ограниченном формате, создающем погрешность представления, но и при выполнении арифметических операций над точными или приближенными исходными числами (заметим, что результаты измерений всегда представлены приближенными числами). Так, например, в арифметике целых чисел, не имеющей погрешности представления исходных чисел, операция деления порождает неправильные дроби (говорят, что множество целых чисел не замкнуто относительно операции деления), которые в формате целых чисел записываются приближенно целыми числами ограниченной точности. Аналогичные погрешности операций могут иметь место при умножении и делении дробных чисел.

Погрешности представления и погрешности операций имеют одну природу, связанную с округлением чисел. Рассмотрим правила округления и величины, характеризующие точность округленных чисел. Округление точного числа А*, содержащего (n+k) R-ичных разрядов, заключается в ограничении его формата n разрядами. При выполнении этой операции желательно обеспечить наибольшую близость округленного числа АR к округляемому числу АR*. На практике используют обычно два способа округления: отбрасывание и симметричное округление. Способ отбрасывания – это просто исключение дополнительных k разрядов округляемого числа из формата без какой-либо коррекции части числа, остающейся в n разрядах. Симметричное округление определяется следующими выражениями соответственно для дробных и целых чисел:

 

AR= ±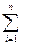ai10R-i , если an+1<R/2 ; AR= ±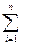ai10R-i + 10R-n, если an+1≥R/2 (8)

AR= ±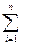ai10Ri , если a-1<R/2 ; AR= ±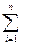ai10Ri , если a-1≥R/2 (9)

При симметричном округлении значение первой из отбрасываемых цифр округляемого числа используется для решения вопроса о коррекции части числа в оставшихся n разрядах. На практике способ симметричного округления для случая an+1=R/2 (a-1=R/2) иногда дополняют правилом Гаусса, в соответствии с которым коррекция оставшейся части числа производится, если цифра an (a0) четная.

Определим абсолютную ошибку округления ΔАR как разность значений округляемого и округленного чисел, а относительную ошибку округления δАR как модуль отношения абсолютной ошибки к значению округляемого числа:

ΔАR= АR* - АR ; δАR= |ΔАR / АR*| (10)

Поскольку в большинстве случаев точное значение округляемого числа неизвестно, то неизвестны и точные величины ошибок в (10). Определим граничную абсолютную Δг и относительную δг ошибки округления следующим образом:

|ΔАR |≤ Δг ; δг= Δг /|АR | (11)

Замена |АR*| на |АR| не вносит в выражение (11) существенной погрешности в значение δ, если Δг<<|АR | . На практике используют по возможности минимальное значение граничной ошибки. Очевидно, что граничная абсолютная ошибка любых R-ичных чисел, представленных в n-разрядном формате, имеет значение Δг= 10R-n Δг=1 соответственно для дробных и целых чисел при способе округления с отбрасыванием и в 2 раза меньшее значение при симметричном округлении. Способ отбрасывания порождает всегда округление числа с недостатком». Поэтому его называют еще несимметричным округлением. Симметричный же способ в зависимости от значения первой отбрасываемой цифры порождает как числа с недостатком», так и числа с избытком», что в процессе многочисленных округлений при вычислениях приводит к компенсации ошибок и повышению точности результата.

В арифметике с фиксированной запятой все числа представляются с одинаковой граничной абсолютной ошибкой. Величина же граничной относительной ошибки зависит от модуля округленного числа и возрастает от максимального числа к минимальному. Малые числа, близкие к машинному нулю, могут иметь высокую относительную ошибку, т.е. имеют низкую точность. Если такие числа участвуют в промежуточных вычислениях, точность результата будет того же порядка. Поэтому при программировании вычислений важно обеспечить требуемую точность представления как исходных чисел, так и промежуточных результатов. Это достигается правильным выбором порядка операций и значности чисел.

Понятие значности имеет важное значение для достижения требуемой точности вычислений. Значность определяет не общее количество цифр в изображении числа, а только количество значащих цифр, т.е. всех верных цифр числа, кроме нулей, стоящих слева в изображении числа. Например, числа 12,3; 0,123; 0,00123 имеют одинаковую значность – по три значащих цифры. Цифры в записи приближенного числа принято считать верными, если граничная абсолютная погрешность представления этого числа не превосходит единицы или половины единицы его младшего разряда. В силу этого определения все цифры округленного числа являются верными, хотя фактически могут не совпадать с соответствующими цифрами точного числа. Значность чисел определяет граничную относительную ошибку их представления: чем выше значность, тем меньше эта ошибка и, следовательно, тем выше точность числа.

В арифметике с фиксированной запятой (в отличие от арифметики с плавающей запятой, см. ниже) повышение значности приводит одновременно к существенному увеличению диапазона представимых чисел, т.е. точность и диапазон чисел оказываются тесно связанными друг с другом. Повышение значности в микропроцессорах с фиксированной разрядностью достигается за счет, как правило, побайтного увеличения формата чисел (байт является структурной единицей, требующей минимальных программных затрат для своей обработки).

В заключение рассмотрим кратко арифметику с плавающей запятой. Эта арифметика снимает ряд проблем, которые существуют в арифметике с фиксированной запятой: увеличение диапазона представления чисел (увеличение разрядности) при сохранении их ограниченной значности, неопределенность прогнозирования вычислений и их масштабируемость и другие. Арифметика с плавающей запятой обеспечивает раздельное представление диапазона и точности чисел (порядка и мантиссы), реализуя их автоматическое масштабирование в процессе вычислений.

Числа с плавающей запятой имеют следующую общую форму представления:

AR=RmARф, m=var (12)

где Rm – характеристика числа, m – целочисленный порядок, ARф – мантисса числа (правильная дробь), определяемая выражением:

ARф= ±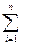aiR-i =±, а1а2…аn, R-n≤|ARф|≤ 1-R-n или ARф=0 (13)

В мантиссе запятая фиксирована перед ее старшим цифровым разрядом, но фактическое положение запятой в представлении числа определяется независимо от мантиссы порядком m и изменяется в зависимости от его величины и знака. Если мантисса меньше единицы, но больше и равна R-1, то такую мантиссу и число с плавающей запятой называют нормализованным. Признаком нормализованности абсолютной величины числа является наличие в старшем цифровом разряде мантиссы ненулевой цифры. Все остальные числа, не удовлетворяющие указанному условию, называют ненормализованными. Например, число 102∙0,1234 нормализовано, а число 103∙0,01234 – ненормализовано. Преимущества нормализованных чисел: а) они определяются единственным образом, б) обеспечивают максимально возможную точность представления чисел в выбранном n-разрядном формате, в) не тратят разряды на изображение незначащих нулей. В нормализованном виде можно представить любое число, отличное от нуля. Для представления же нуля используют несколько вариантов: 1) ARф=0 и m – произвольно, 2) ARф произвольно, m=mmin, 3) ARф=0, m=0, 4) ARф =0, m=mmin.

Машинное представление формата чисел с плавающей запятой, в отличие от формата чисел с фиксированной запятой, содержит помимо разряда знака и n разрядов цифровой части числа – мантиссы, дополнительно разряд знака и k цифровых разрядов порядка. Диапазон нормализованных чисел практически не зависит от разрядности мантиссы, а определяется в основном величиной основания системы счисления и разрядностью порядка. Точность представления чисел с плавающей запятой определяется теми же формулами, что и для чисел с фиксированной запятой. Граничная абсолютная ошибка этих чисел в отличие от чисел с фиксированной запятой непостоянна и зависит не только от разрядности мантиссы и метода ее округления, но и от величины порядка. Граничная же относительная ошибка представления чисел с плавающей запятой не зависит от величины порядка, определяется разрядностью мантиссы и практически одинакова для любых чисел, как малых, так и больших (этот вывод справедлив только для нормализованных чисел). Таким образом, в формате числа с плавающей запятой диапазон и точность чисел отделены друг от друга: разрядность мантиссы определяет точность представления чисел, а разрядность порядка – их диапазон. Арифметические операции над числами с плавающей запятой выполняют действия как над мантиссами, так и над порядками, причем те и другие представляются в виде знаковых чисел.

Рассмотренные способы и форматы машинного представления рациональных чисел показывают, что требуемую точность представления чисел (результатов измерений) и их обработки можно достичь, в отличие от аналоговых представлений, за счет достаточно простых средств.

Хранение и передача чисел в цифровых системах

В цифровых системах числа не только подвергаются той или иной арифметической обработке, но хранятся в цифровой памяти и передаются по линиям или каналам связи между разными частями системы для выполнения в них различных операций. Как обеспечить требуемую точность арифметической обработки, ясно из предыдущего подраздела. Рассмотрим вопросы обеспечения требуемой точности в операциях машинного хранения и передачи чисел.

Исходное число, поступающее в цифровую систему, или промежуточное (конечное) число, образующееся в системе в результате арифметической обработки, имеет определенную разрядность n (пусть это двоичная разрядность нормализованной мантиссы числа, представленного в формате с плавающей запятой), которая определяет точность машинного представления числа (очевидно, что относительная погрешность представления точного числа в рассматриваемом случае не превышает 2-n). При представлении приближенного числа (например, результата измерения), точность которого не превышает 2-k, k<n, лишние» разряды (n-k) обеспечивают хранение приближенного числа по точности с запасом» с целью исключения потери значности (точности) приближенного числа в процессе арифметической обработки, если последняя будет иметь место. Для конечного же результата арифметической обработки точность его представления, в общем случае, не может быть выше точности исходного числа, т.е. должна иметь не более k разрядов. Это требование называют золотым правилом приближенных вычислений».

Таким образом, в цифровых системах, обрабатывающих числовые данные результатов измерений, точность машинного представления (хранения) этих данных на входе и выходе системы должна соответствовать точности этих данных, т.е. быть не ниже ее. Точность представления промежуточных данных зависит от вида и количества выполняемых арифметических операций и может быть определена стандартными способами вычислительной математики. При хранении чисел в цифровой твердотельной памяти современных цифровых систем следует учитывать высокую стабильность во времени такого хранения, обеспечивающего сохранение данных без изменения практически на протяжении всего срока службы этой памяти. Вместе с тем, для повышения достоверности хранения числовых данных (особенно в случае технического отказа памяти) целесообразно периодически производить репликацию хранимых данных в резервные хранилища как внутри цифровой системы, так и вне ее.

Передача данных в цифровых системах производится по цифровым интерфейсам, к которым, в частности, относятся интерфейсы физического уровня RS232, RS485, CL и многие другие. Передача производится по цифровым протоколам, имеющим, как правило, многоуровневую архитектуру (в простейшем случае – дополнительно к физическому уровню используется лишь один канальный уровень). На каждом уровне передачи числовых данных обеспечивается их защита от искажений за счет применения контрольных разрядов и кодов. В процессе приема данных обеспечивается их контроль на наличие ошибок, а также используются различные другие методы достоверизации данных. В том случае, когда измерительные данные накапливаются длительное время в точке измерения (в цифровой памяти СИ), то одним из наиболее эффективных методов обеспечения их достоверности при передаче в другие части цифровой системы является метод повторных запросов и сравнения результатов приема данных от этих запросов (очевидно, например, что если результаты двух или более запросов одних и тех же числовых данных совпали, то можно говорить о высокой достоверности передачи данных).

Отметим, что операции арифметической обработки, хранения и передачи чисел обладают по отношению к аналогичным операциям аналоговых и дискретных систем высокой стабильностью во времени (их характеристики со временем практически не изменяются) и высокой достоверностью, которую, как и точность вычислений, не сложно увеличить за счет дополнительной программной обработки. Если для СИ метрология вводит понятие межповерочного интервала, что связано с меняющейся во времени метрологической стабильностью этих средств, то для цифровых систем их метрологическая стабильность постоянна во времени и поэтому не требует периодических поверок. Для цифровых систем возможет технический (выход из строя), но не метрологический отказ, который характерен для аналоговых и дискретных ИС в связи с постепенной деградацией их аналоговых элементов. Для цифровых систем, если отлаженная программа арифметической обработки или передачи данных работает, то она работает всегда и одинаковым образом, пока работает само техническое средство. Программы, а в цифровых системах все виды обработки выполняются программным путем, не ломаются» (хотя недоотлаженные программы могут работать с ошибками).

 Основные понятия метрологии цифровых измерений

Введем новые понятия метрологии цифровых измерений, используя в максимальной степени устоявшиеся понятия традиционной метрологии, приведенные в РМГ 29-99 [10].

Определение (1). Цифровой результат измерения физической величины – числовое значение величины, полученное путем ее измерения, представленное в позиционной системе счисления в виде рационального числа определенного формата с известной точностью и доверительной вероятностью.

Примечания

1 В современных технических системах используются преимущественно двоичная, восьмеричная, шестнадцатеричная и десятичная (или двоично-десятичная) системы счисления и два формата представления рациональных чисел: с фиксированной и с плавающей запятой (точкой).

2 Цифровой результат измерения может регистрироваться в цифровом регистре, в цифровой памяти (базе данных), на цифровом табло, на цифровой печати, на других аудио- и видеосредствах отображения и документирования данных.

Определение (2). Цифровое измерение физической величины – измерение, результат которого представлен в цифровом виде (цифровой результат).

Примечания

1 Цифровому измерению физической величины противопоставляется нецифровое измерение, к которому относятся аналоговые и дискретные измерения, результаты которых представляются в виде аналоговых сигналов, кодов или отсчетов соответствующей шкалы.

2 Любое измерение оканчивается там и тогда, где и когда появляется цифровой результат измерения, независимо от его дальнейшего использования.

3 Цифровое измерение – это всегда прямое измерение (в строгом смысле понятия измерения измерение всегда прямое). Понятие косвенного измерения в метрологии цифровых измерений для цифровых операций отсутствует, так как операции преобразований цифровых результатов измерений не являются измерением, а относятся к операциям неизмерительного назначения (например, хранения, передачи, вычисления и т.п.).

Определение (3). Цифровое средство измерений (ЦСИ) – СИ, выполняющее цифровое измерение.

Примечание - Цифровому СИ противопоставляется нецифровое СИ, которое выполняет нецифровые измерения.

Определение (4). Цифровой измерительный канал (ЦИК) – цепь последовательно соединенных СИ, образующих путь прохождения измерительной информации от входа цепи к выходу и предназначенных для измерения одной физической величины с представлением результатов ее измерений на выходе ИК в цифровом виде.

Примечания

1 Цифровому ИК противопоставляется нецифровой ИК, содержащий нецифровые СИ.

2 В состав ЦИК входит в качестве выходного устройства цифровое СИ, а в качестве исходных и промежуточных – нецифровые СИ. В простейшем случае ЦИК содержит одно цифровое СИ.

Определение (5). Цифровая измерительная система (ЦИС) – совокупность цифровых ИК и иных технических средств неизмерительного назначения, объединенных единым алгоритмом функционирования, предназначенная для измерений, а также выполнения иных операций неизмерительного назначения с целью определения значений одной или нескольких физических величин или их функций.

Примечания

1 Цифровой ИС противопоставляется нецифровая ИС, в которой все ИК или их часть являются нецифровыми. В цифровой ИС все ИК являются цифровыми.

2 Цифровая ИС в простейшем случае содержит один ЦИК и одно техническое средство неизмерительного назначения, конструктивно обособленное от ИК.

3 К техническим средствам неизмерительного назначения относятся средства, не выполняющие измерений. Такими средствами являются компьютер (в том случае, если он не реализует с помощью встроенных в него технических средств аналого-цифровых и дискретно-цифровых измерительных преобразований входных сигналов), цифровой накопитель (цифровая память), монитор, принтер, модем, каналы и линии связи и другие устройства.

Определение (6). Метрология цифровых измерений (цифровая метрология) – наука о цифровых измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.

Примечания

1 Цифровая метрология отличается от традиционной метрологии тем, что имеет дело только с цифровыми измерениями. Она может рассматриваться как новое направление традиционной метрологии, имеющее с ней как сходство, так и отличия. Появление этого направления метрологии связано с массовым распространением современной цифровой технологии во все области практики, включая измерения.

2 Традиционная метрология, частично входящая в цифровую метрологию, распространяет свою сферу влияния только до уровня получения цифрового результата измерения, т.е. в рамках СИ или ЦИК. В их отношении сохраняют применимость все традиционные метрологические понятия и положения, включая понятие метрологического контроля.

3 За пределами цифрового результата измерения кончается действие традиционной метрологии, так как с появлением этого результата заканчивается сам процесс измерения. Дальнейшие преобразования этого результата относятся не к области измерений, а к области цифровых информационных технологий (вычислительной техники, программирования, техники связи и т.п.).

4 Цифровая метрология, в отличие от традиционной метрологии, рассматривает все дальнейшие технологические процессы преобразования цифрового результата измерений как операции неизмерительного характера. Поэтому технические средства, выполняющие эти операции, не рассматриваются как СИ, хотя к ним и предъявляются определенные требования по точности и достоверности выполнения соответствующих неизмерительных операций.

Определение (7). Цифровой контроль технических средств – совокупность работ, в ходе выполнения которых устанавливаются или подтверждаются точностные характеристики технических средств неизмерительного назначения, используемых в составе цифровых измерительных систем.

Примечания – К цифровому контролю относятся цифровая экспертиза, цифровая поверка и цифровая аттестация технических средств неизмерительного назначения.

Определение (8). Точностная характеристика технического средства – характеристика, определяющая точность и достоверность цифровых преобразований, выполняемых техническим средством.

Примечания

1 Точностные характеристики зависят от назначения и состава цифровых преобразований соответствующего технического средства. Технические средства могут подразделяться по составу цифровых преобразований на вычислительные (компьютер, контроллер), хранения (память), отображения (табло, дисплей, монитор), документирования (принтер), передачи (линии и каналы связи) и т.п. и (или) их комбинации.

2 Точностная характеристика вычислителя определяет точность и достоверность вычислительных операций, включая форматы представления чисел, методы их округления и контроля правильности операций.

3 Точностная характеристика средства хранения определяет его разрядность, методы контроля записи, чтения и хранения чисел и их временную стабильность.

4 Точностная характеристика средства отображения или документирования определяет форматы представления чисел и методы их округления при выводе чисел из памяти для отображения или документирования.

5 Точностная характеристика средства передачи определяет скорость, задержку и надежность приема/передачи чисел, включая методы обнаружен6ия, контроля и исправления ошибок.

Определение (9). Цифровая экспертиза технических средств – анализ и оценивание экспертами-метрологами на основании соответствующей документации достаточности точностных характеристик технических средств неизмерительного назначения, используемых в составе цифровых измерительных систем.

Примечание – Результатом цифровой экспертизы технических средств является экспертное заключение соответствующей метрологической службы.

Определение (10). Цифровая поверка технических средств – испытание технических средств на соответствие их реальных точностных характеристик характеристикам, заявленным в соответствующей технической документации.

Примечания

1 Для технических средств неизмерительного назначения достаточна первичная поверка, связанная с их цифровой аттестацией. Необходимость в периодических поверках (как для средств измерений) отсутствует.

2 Цифровая поверка должна проводиться согласно соответствующей методике цифровой поверки, которая должна входить в комплект технической документации технического средства неизмерительного назначения, используемого в составе цифровой измерительной системы.

3 При цифровой поверке могут использоваться как автоматические способы генерации чисел заданной точности (путем применения генераторов чисел, подключаемые к техническому средству по цифровому ин6терфейсу), так и ручные способы (путем записи чисел в память технического средства через клавиатуру).

Определение (11). Цифровая аттестация технических средств – признание метрологической службой узаконенным для применения технических средств неизмерительного назначения в составе конкретных цифровых измерительных систем.

Примечания

1 Цифровая аттестация включает в себя цифровую экспертизу и при необходимости первичную поверку соответствующих технических средств.

2 Результатом цифровой аттестации технических средств является соответствующее свидетельство, выдаваемое метрологической службой.

Введенные основные понятия цифровой метрологии примем за основу предложений по метрологической аттестации цифровых ИС и их разновидности – цифровых АСКУЭ.

 Об аттестации цифровых АСКУЭ

Типовая структурная схема цифровой АСКУЭ приведена ниже на рис.2 [5].

Эта схема содержит три уровня: а) первый, или нижний уровень, на котором (при необходимости) устанавливаются масштабные преобразователи – измерительные трансформаторы тока и напряжения и электронные электросчетчики, б) второй, или промежуточный уровень, на котором (при необходимости) устанавливается устройство сбора и передачи данных - УСПД, в) третий, или верхний уровень, на котором (при необходимости) устанавливается компьютер с программным обеспечением АСКУЭ. Такая модель цифровой АСКУЭ в наибольшей мере соответствует современным структурам реальных цифровых АСКУЭ.

Вместе с тем, возможны варианты этой схемы, в которых, например, в одном случае, на первом уровне используются электронные электросчетчики непосредственного включения по току и напряжению (при напряжении не выше 0,4 кВ и токе не выше 100 А), не требующие применения измерительных трансформаторов тока и напряжения. Во втором случае на втором уровне может отсутствовать УСПД (или наоборот применяться два последовательно соединенных УСПД: ведущее и ведомое), а счетчики подключаются по цифровым интерфейсам к компьютеру верхнего уровня и т.п. Можно представить и схему будущей цифровой АСКУЭ, в которой функции счетчиков перенесены на уровень цифровых измерительных трансформаторов тока и напряжения. В этом случае отпадает необходимость в счетчиках, а цифровые выходы измерительных трансформаторов подключаются непосредственно к УСПД или при его отсутствии – к компьютеру.

В любом варианте в цифровой АСКУЭ присутствуют две группы технических средств: цифровые ИК и средства неизмерительного назначения. К первым относятся такие средства измерений и учета, как измерительные трансформаторы и электронные электросчетчики, а ко вторым – УСПД, компьютеры с программным обеспечением АСКУЭ, линии и каналы связи. Первые выполняют аналоговые и цифровые измерения, а вторые – только цифровые операции неизмерительного характера: хранения, передачи, обработки, отображения и документирования данных учета.

Особенностью АСКУЭ любого вида является выполнение операций синхронного измерения количества электроэнергии в территориально распределенных точках учета, в которых устанавливаются электронные электросчетчики, имеющие встроенные часы и календарь. Эти часы должны синхронизироваться от единого источника точного времени. Такая синхронизация может выполняться как параллельно и независимо для каждого электросчетчика, например, путем приема счетчиком радиосигнала точного времени, так и путем передачи команд установки времени на счетчики по каналам связи через компьютер и УСПД. Возникает вопрос: не становятся ли средства неизмерительного назначения, такие, например, как УСПД, компьютер или канал связи, средствами измерения времени из-за необходимости передачи сигналов точного времени и синхронизации измерений электроэнергии? Ведь УСПД и компьютер также имеют встроенные часы и календарь, которые используются для инициирования выполнения различных операций с привязкой их к меткам времени (например, часовой или суточной меткам)?

Отметим, что все процессы измерения электроэнергии, в том числе с привязкой к сигналам времени, производятся исключительно в электронных электросчетчиках, которые относятся к СИ со всеми вытекающими отсюда последствиями. УСПД и компьютеры обрабатывают далее только цифровые результаты измерений счетчиков, в том числе с привязкой их ко времени счетчиков (а не ко времени УСПД или компьютера), т.е. УСПД и компьютер, несмотря на наличие своих встроенных часов, не выполняют операций измерений ни электроэнергии во времени, ни самого времени. Их встроенные часы носят не измерительный, а вспомогательный, справочный характер. Они могут, вообще говоря, существенно отличаться по своим значениям от часов счетчиков и это не вызовет ошибок в вычислениях электроэнергии, а только создаст неудобства. Поэтому требования к точности хода часов УСПД и компьютеров в АСКУЭ носят не метрологический, а общий характер.

В случае передачи команд точного времени для синхронизации часов счетчиков через канал связи, УСПД и компьютер последние вносят в процесс передачи определенную задержку, которая может повлиять на точность хода часов счетчиков. Эта задержка может быть малой или большой, но известен рутинный алгоритм ее компенсации (поправки), который сводит ее на нет». И в отношении передачи сигналов точного времени указанные средства не удается представить как СИ.

Таким образом, и с учетом выполнения в цифровых АСКУЭ операций синхронного измерения электроэнергии сохраняется ранее введенное разделение всех технических средств в АСКУЭ на СИ и средства неизмерительного назначения. В соответствии с указанной структурой цифровой АСКУЭ методика ее метрологической аттестации должна состоять из двух частей: метрологической аттестации ЦИК и цифровой аттестации технических средств неизмерительного назначения. Первая часть методики должна базироваться на типовых методиках аттестации ИС, а вторая – на положениях цифровой метрологии, приведенных выше, и методах современных цифровых информационных технологий.

 Заключение

В настоящей работе представлены результаты нового подхода к метрологии цифровых ИС и цифровых АСКУЭ. По существу предложено и обосновано новое направление в метрологии ИС, которое отделяет процессы измерения от всех иных дополнительных процессов неизмерительного характера (передачи, хранения, обработки, отображения и документирования цифровых данных). На пути становления цифровой метрологии предстоит еще преодолеть психологическую инерцию многих метрологов, привыкших относить к измерениям и СИ все, что находится рядом с ними. Такой устарелый подход вносит только путаницу в метрологию ИС, создает иллюзию обеспечения единства измерений и ведет к необоснованным материальным, финансовым и временным затратам общества. В связи с появлением метрологии цифровых измерений необходимо будет в дальнейшем пересмотреть и уточнить ряд базовых понятий метрологии, в частности, таких как измерение, косвенное измерение, средство измерения и других. Использование метрологии цифровых измерений для создания методик метрологической аттестации цифровых АСКУЭ позволит упростить и упорядочить процессы создания и эксплуатации таких систем, снизив существенно расходы общества на их метрологический контроль.

Литература

1 Гуртовцев А.Л. Современные принципы автоматизации энергоучета в энергосистемах. - Промышленые АСУ и контроллеры, №4,2003.

2 Гуртовцев А.Л., Забелло Е.П. Приборный учет электрической энергии. Система новых взглядов. - Энергетика и ТЭК, № 3,4, 2003.

3 Гуртовцев А.Л. Правила приборного учета электроэнергии. Глобальный проект белорусских энергетиков. - Новости электротехники, № 6,2004.

4 Концепция приборного учета электрической энергии в Республике Беларусь. - Энергетика и ТЭК, № 12,2005, № 1, 2006.

5 Гуртовцев А.Л. . О метрологии цифровых АСКУЭ и границах метрологической экспансии. - Электрика, №10, 2006.

6 Гуртовцев А.Л. Современные принципы приборного учета электроэнергии. Опыт Беларуси. - Сборник докладов десятой научно-практической конференции-выставки Метрология электрических измерений в электроэнергетике», 26-30 марта 2007 г., Москва.

7 Нормативно-правовая и нормативно-техническая база метрологии электрических измерений в электроэнергетике/ Составители: Комкова Е.В., Калашник Л.Н., Туркина О.В – Сборник докладов десятой научно-практической конференции-выставки Метрология электрических измерений в электроэнергетике», 26-30 марта 2007 г., Москва.

8 ГОСТ 8.009-84 ГСИ. Нормируемые метрологические характеристики средств измерений.

9 ГОСТ Р 8.596-2002 ГСИ. Метрологическое обеспечение измерительных систем. Основные положения.

10 РМГ 29-99 ГСИ. Метрология. Основные термины и определения.

11 МИ 1317-2004 ГСИ. Результаты измерений и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров.

12 МИ 2439-97 Рекомендация. ГСИ. Метрологические характеристики измерительных систем. Номенклатура. Принципы регламентации, определения и контроля.

13 МИ 2440-97 Рекомендация. ГСИ. Методы экспериментального определения и контроля измерительных систем и измерительных комплексов.

14 МИ 2539-99 Рекомендация. ГСИ. Измерительные каналы контроллеров, измерительно-вычислительных, управляющих, программно-технических комплексов. Методика поверки.

15 МИ 2891-2004 ГСИ. Рекомендация. Общие требования к программному обеспечению средств измерений.

16 МИ 3000-2006 ГСИ. Системы автоматизированные информационно-измерительные коммерческого учета электрической энергии. Типовая методика поверки.

17 РД 34.11.206-94 Методические указания. Информационно-измерительные системы. Методика обработки экспериментальных данных метрологической аттестации

18 РД 34.11.202-95 Методические указания. Измерительные каналы информационно-измерительных систем. Организация и порядок проведения метрологической аттестации.

19 РД 34.11.333-97 Учет электрической энергии и мощности на энергообъектах. Типовая методика выполнения измерений количества электрической энергии.

20 РД 34.11.334-97 Учет электрической энергии и мощности на энергообъектах. Типовая методика выполнения измерений количества электрической мощности.

21 РД 153-34.0-11.204-97 Методика приемки из наладки в эксплуатацию измерительных каналов информационно-измерительных систем.

22 РД-34.11.114-98 Автоматизированные системы контроля и учета электроэнергии и мощности. Основные нормируемые метрологические характеристики. Общие требования.

23 РД 153-34.0-11.117-2001 Основные положения. Информационно-измерительные системы. Метрологическое обеспечение.

24 ГОСТ 8.437-81 ГСИ. Системы информационно-измерительные. Метрологическое обеспечение. Основные положения.

25 МИ 219-80 ГСИ. Информационно-измерительные системы. Организация и порядок проведения метрологического надзора.

26 МИ-202-80 ГСИ. Методика. Метрологические характеристики измерительных систем. Принципы регламентации и контроля. Основные положения .

27 МИ 222-80 ГСИ. Методика расчета метрологических характеристик измерительных каналов информационно-измерительных систем по метрологическим характеристикам компонентов.

28 МИ 2002-89 ГСИ. Рекомендация. Государственная система обеспечения единства измерений. Системы информационно-измерительные. Организация и порядок проведения метрологической аттестации.

29 Закон Республики Беларусь от 20 июля 2006 г. № 163 -З "Об обеспечении единства измерений".

30 СТБ 8004-93 Система обеспечения единства измерений Республики Беларусь. Метрологическая аттестация средств измерений

31 МИ 200-80 Методика контроля метрологических характеристик измерительных информационных систем встроенными средствами контроля. Основные положения.

32 ГОСТ 26.203-81 Комплексы измерительно-вычислительные. Признаки классификации. Общие требования.

33 ГОСТ 4.199-85 Система показателей качества продукции. Системы информационные электроизмерительные. Комплексы измерительно-вычислительные. Номенклатура показателей.

34 МИ 1999-89 Методические указания. Государственная система обеспечения единства измерений. Системы измерительные информационные. Общие требования к метрологическому обеспечению

35 МИ 2168-91ГСИ. Рекомендация. Системы измерительные информационные. Методика расчета метрологических характеристик измерительных каналов по метрологическим характеристикам линейных аналоговых компонентов.

36 ГОСТ 22315-77 Средства агрегатные информационно-измерительных систем. Общие положения.

37 ГОСТ 22316-77 Средства агрегатные информационно-измерительных систем. Общие требования к организации взаимодействия средств при построении систем.

38 Гуртовцев А.Л., Гудыменко С.В. Программы для микропроцессоров. – Минск, Вышэйшая шк., 1989.

Справка

Статья опубликована в журнале

Современные технологии автоматизации (СТА), № 1, №2, 2008 (Россия).

По итогам 2008 г. удостоена 2-ой Премии в конкурсе СТА “Лучшая статья года”.