Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования

Портнягин Н. Н., Пюкке Г. А.,

2.2.3. Построение совокупности аналитических выражений функций передачи каналов диагностирования

Этап формирования массива основных диагностических признаков начинается с приведения ОД к многополюсной системе. Все узлы диагностируемой электрической цепи рассматриваются как внешние полюсы, потенциально возможные для использования при проведении диагностических процедур. Записывается система узловых уравнений

G^(у)  U₀ = I₀ ,

где G^(у) - укороченная матрица узловых проводимостей; U₀ – матрица-столбец узловых напряжений; I₀ - матрица - столбец суммы токов источников тока и источников  тока,  преобразованных  из  источников ЭДС,  подключенных к

 i – му узлу. Используя понятие обобщенной ветви I = I + J; U = U – Е, и систему узловых уравнений : АI+АJ=0 , где А  - матрица инциденций;

I – матрица-столбец токов ветвей; J – матрица-столбец токов источников тока; Е – матрица-столбец ЭДС источников ЭДС; U – матрица-столбец полюсных напряжений, можно получить выражение G^(у) удобное к применению при машинной обработке данных: АI = – АJ; но I = G^(у) U, где G^(у)  – диагональная матрица проводимостей ветвей. Тогда: А G^(у) U = – АJ, но U = U+Е, а U = А^t U₀ ; то U = А^t U₀ + Е; и  АYA^t = - A( J + YE ), где: -А( J + YE ) = I₀ ,  Соответственно: AYA^t = Y_узл . Необходимо  отметить, что для построения всего массива коэффициентов передачи сигналов целесообразно использовать топологические методы: метод формирования миноров определителя матрицы узловых проводимостей и метод напряжений ветвей дерева. Согласно первому методу весь массив коэффициентов передачи сигналов многополюсной системы подразделяется на три подмножества М₁, М₂, М₃, имеющие следующие коэффициенты передачи K_s – k , K_fg-lm , K _s – l m и  K _{f g – k}. Для получения аналитических выражений основных диагностических признаков записывается выражение для напряжения внешнего i - го полюса многополюсной системы: U_i = Δ_i / Δ , где Δ -определитель матрицы G^(у);  Δ_i  – определитель полученный из Δ  путем замены i-го столбца столбцом полюсных токов (  i ₁ ,  i ₂ , …..i _{n – 1} ) ^t . Разлагается определитель Δ_i по элементам i-го столбца:  U_i = i₁ Δ_1i / Δ + i ₂ Δ _{2 i} / Δ + ………+ i _s Δ _{s i} / Δ + …………+ i _n Δ _{n i} / Δ. Тогда при возбуждении соответствующего входа (например на полюсе s) в цепи возникает только один полюсный ток i_s  и общее уравнение обращается в частное: U _i = i _s Δ _{s i} / Δ, соответственно: U _k = i _s Δ _sk / Δ ;U _s = i _s Δ _ss / Δ . Взяв отношение напряжений, получим:

1. Коэффициент передачи по напряжению К _{s - k}  от входа s  к выходу k, инцидентных опорному полюсу равен: K_s - k ,= U _k / U _s  =  ( i _s Δ _s k / Δ ) / (i _sΔ _s s / Δ ) = Δ _s k / Δ_ss , где Δ _{s k} - определитель, полученный из определителя Δ  вычеркиванием s-й строки и k-го столбца; Δ _{s s} – соответственно, s-й строки и s- го столбца.

2. Коэффициент передачи по напряжению от входа fg к выходу lm, неинцидентных нулевому полюсу: K_fg-lm = (U_l – U_m) / (U_f – U_g) = Δ _{( f + g ) ( l + m )}  / Δ  _{( f + g ) ( f + g )} , где Δ _{( f + g ) ( l + m )}  - определитель у которого строка f  перенесена в строку g, а столбец l перенесен в столбец m; Δ _{( f + g ) ( f + g )}  – определитель,  у которого строка  f перенесена в строку g, а столбец f перенесен в столбец g.

3. Коэффициент передачи по напряжению от входа s инцидентного нулевому полюсу к выходу lm неинцидентному нулевому полюсу:

K _{s – l m} = (U _l – U _m ) / U _s = (Δ _{s l} – Δ _{s m} ) / Δ _{s s} = Δ _{s ( l + m )}  / Δ  _{s s}  . 

4. Коэффициент передачи от входа fg,  неинцидентного нулевомуполюсу, к выходу k,  инцидентному нулевому полюсу:

K _{f g – k} = U _k / (U _f – U _g ) = Δ _{( f + g ) k} / (Δ _{( f + g ) f} – Δ _{( f + g ) g}  ) =  Δ _{( f + g ) k} / Δ _{( f + g ) ( f + g )} .

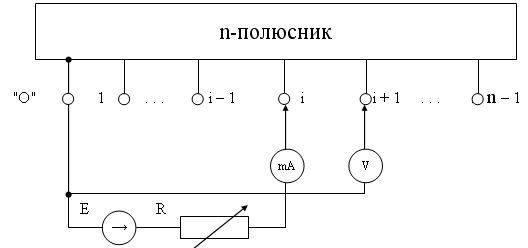
Если диагностируется электрическая цепь с априори неизвестной топологией, то G^(у) может быть получена практически с использованием элементов теории планирования эксперимента. Для ее формирования в исследуемом многополюснике (Рис. 2.6)  между узлами 0  и 1, n-1  поочередно включается регулируемый источник электроэнергии и каждый раз устанавливается значение входного задающего тока равное единице. Производя при каждом очередном включении замеры напряжений между узлами 0 и 1, n-1, можно составить систему уравнений для потенциалов, искусственно сформировав справа единичную диагональную матрицу: G^(у) U^(у) = 1 G^(у) U^(у) [ U^(у) ] ^-1 = 1 [ U^(у) ] ^-1 G^(у) = [ U^(у) ] ^-1 , т.е. для получения G^(у)достаточно обратить полученную экспериментально матрицу узловых напряжений U^(у). На основании полученной матрицы узловых проводимостейG^(у) формируется множество М диагностических признаков. Если ОД содержит многополюсные компоненты, то матрица G^(у)  объекта диагностирования может быть получена способом наложения матриц многополюсных компонент, содержащихся в ОД, на матрицу объекта диагностирования, а ее элементы выражены через полюсные проводимости составляющих многополюсных компонент [29].

 .

Рис. 2.6. Схема коммутаций при формировании матрицы узловых проводимостей

Рассмотренная процедура получения исходной матрицы узловых проводимостей основана на представлении всех узлов в виде полюсов. Наличие полюсов, токи которых равны нулю, позволяет изменять порядок матрицы узловых проводимостей цепи в зависимости от размера выбранной СЕ, определяемого глубиной поиска дефекта.

Следует отметить, что использование тестового диагностирования электрической цепи, представленной совокупностью пассивных элементов, при отсутствии рабочих сигналов и источника рабочего питания, существенно упрощает процедуру формирования множества прямых диагностических признаков т.к. при таком подходе  элементы электронных цепей (биполярные, полевые транзисторы, тиристоры  и т.д.) не рассматриваются как управляемые источники энергии, что существенно упрощает расчет и последующее диагностирование.