Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.1.2. Гравитационное поле
Одной из основных количественных характеристик гравитационного поля, создаваемого массой М – источником гравитационного поля, служит его напряжённость – векторная величина 
(рис. 1.2), равная отношению силы 
гравитационного поля к массе m, испытывающей воздействие этой силы – пробной массе.
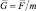– векторная форма равенства;
G = F/m – скалярная форма равенства.
То есть, напряжённость гравитационного поля можно воспринимать как силу этого поля, воздействующую на единицу пробной массы. В свою очередь, согласно второму закону Ньютона:
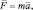
или F = ma,
где 
и а – вектор ускорения и абсолютное значение ускорения пробной массы соответственно. Поэтому
,
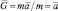или G = ma/m = а.
Таким образом, под действием сил гравитационного поля свободная материальная точка приобретает ускорение, равное напряжённости этого поля.
Сила взаимодействия между массами подчиняется закону всемирного тяготения И. Ньютона:
Между всякими двумя материальными точками действуют силы взаимного притяжения, которые прямо пропорциональны массам точек (m1, m2) и обратно пропорциональны квадрату расстояния (r) между ними:
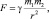
где γ – гравитационная постоянная (γ = 6,67∙10–11 Н∙м2/кг2).
Значит, напряжённость гравитационного поля создаваемая массой m1 может определяться равенством:
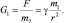
Если источником гравитационного поля является m2, то m1 – пробная масса:
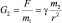
или в векторной форме:
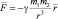[4];
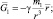
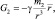
где 
– радиус-вектор, направленный от массы, воспринимаемой как источник гравитационного поля к пробной массе.
Потенциальная энергия взаимодействия (Еп) масс m1 и m2 определяется равенством:
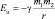[5].
Если напряжённость – отношение силы взаимодействия к пробной массе – является силовой количественной характеристикой источника гравитационного поля, то отношение потенциальной энергии взаимодействия Еп к пробной массе m2 является энергетической количественной характеристикой источника гравитационного поля m1, и называется Ньютоновским гравитационным потенциалом (φ):
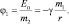
В случае, когда в качестве источника гравитационного поля рассматривают m2, масса m1 воспринимается как пробная:
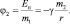
Несмотря на то, что Земля своим гравитационным полем притягивает к себе Луну, ночное светило на Землю не падает. Это происходит потому, что Луна не покоится, а движется с постоянной скоростью вокруг Земли в направлении, перпендикулярном ускорению луны, направленном к Земле. В результате приближение Луны к Земле, вызванное ускорением 
, компенсируется удалением, обусловленным перпендикулярной скоростью 
, что и приводит к неизменности абсолютного значения расстояния между Землёй и Луной. Если приближённо считать, что луна движется вокруг Земли по строго круговой орбите, то:
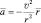
или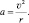 
При этом, вектор 
называется центростремительным ускорением, а противоположный вектор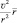 
называют центробежным ускорением. Соответственно, для объекта, движущегося по окружности, произведение 
называется центростремительной силой, а вектор, определяемый равенством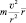 
– центробежной силой. Центростремительная сила гравитационного поля воздействует на пробную массу, а центробежная сила воздействует на связь между источником гравитационного поля и пробной массой. Скорость v тела, движущегося по окружности, нередко называют линейной скоростью, с тем, чтобы не путать её с угловой скоростью (
), абсолютное значение которой определяется равенством
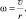
Варианты представления размерности угловой скорости, рассчитанной по приведённой формуле, выглядят следующим образом:
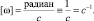
Скорость вращения, составляющая один оборот за секунду, в указанных единицах измерения равна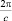 
. Направление угловой скорости можно определять по правилу буравчика. Поскольку, согласно закону Всемирного тяготения
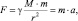
где а – ускорение пробной массы m, то:
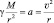
или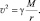 
Таким образом, мы получили зависимость скорости вращения космического объекта от массы центра этого вращения и расстояния до него.
Вам известно, что подобно тому, как Луна вращается вокруг Земли, Земля вращается вокруг Солнца. Но и само Солнце вращается вокруг центра нашей галактики, называемой Млечный Путь. При этом, если вращение Луны вокруг Земли или Земли вокруг Солнца подчиняется последнему уравнению, то вращение Солнца вокруг центра Млечного Пути этому уравнению не подчиняется. Скорость вращения Солнца оказывается существенно большей, чем должна быть при той массе, которая наблюдается в нашей галактике. Подобное явление было обнаружено и для других звёзд, и для других галактик. То есть, оказалось, что массу галактик представляют не только звёзды, планеты, кометы и прочие наблюдаемые тела, но и материя, неизвестной природы никак не наблюдаемая. Она получила название «тёмная материя»
Тёмная материя – это неизвестное вещество, участвующее только в гравитационном взаимодействии.
Кроме того, выяснилось, что между массами, помимо сил притяжения, действуют и силы отталкивания, проявляющиеся на очень больших «космических» расстояниях. В настоящее время достоверно установлено, что Вселенная не просто расширяется, а расширяется с ускорением. То есть, расстояние между галактиками увеличивается во времени с возрастающей скоростью. Обнаруженное ускорение свидетельствует о воздействии на галактики какой-то силы, существовании Во Вселенной неизвестной ранее энергии, называемой «тёмная энергия».
Тёмная энергия – это энергия отталкивания между массами, проявляющаяся на больших «космических» расстояниях.
Примеры решения задачи
Задача
Оценить массу Земли, если известно, что её средний радиус 6371 км, а вблизи поверхности ускорение свободного падения составляет 9,8 м/c2.
|
Дано: |
Решение
|
|
М – ? |
|
;
;M = 9,8∙63712∙106/6,67∙10–11 ≈ 6,0∙1024 кг.
Ответ: M ≈ 6,0∙1024 кг.
Задачи для самостоятельного решения
1. Оцените абсолютное значение силы притяжения своего тела к земле, если ускорение свободного падения (g) равно 9,8 м/c2.
2. Рассчитайте силу притяжения между Землёй и луной, а также между Землёй и солнцем, если среднее расстояние до луны составляет 384 467 км, а до солнца 149,6 миллиона километров. Масса луны 7,35∙1022 кг, а масса солнца 2∙1030 кг. Оцените напряжённость гравитационного поля, создаваемого луной в точке расположения Земли и напряжённость гравитационного поля, создаваемого солнцем в этом же месте.
3. Оцените абсолютные значения:
– Ньютоновского гравитационного потенциала земли у её поверхности;
– потенциальной энергии взаимодействия Земли и своего тела.
4. Запишите в виде формулы зависимость φ от G.
5. Рассчитайте линейную скорость вращения планеты вокруг звезды, если радиус вращения составляет 1011 м, а центростремительное ускорение 2,25∙103 м/c2. Оцените абсолютное значение угловой скорости вращения этой планеты вокруг своей звезды. Выразите астрономический год этой планеты в единицах земных суток.
6. Оцените массу тёмной материи дисковидной галактики, диаметр которой составляет 9,5∙1020 м, а суммарная масса всех звёзд и планет 4,0∙1044 кг. Одна из звёзд этой галактики, расположенная от центра на расстоянии радиуса (4,75∙1020 м), вращается вокруг этого центра со скоростью 1,7∙107 м/c. С какой линейной скоростью вращалась бы эта звезда в отсутствие тёмной материи? Рассчитайте наблюдаемую работу, совершаемую силами тёмной энергии при дальнейшем удалении рассматриваемой галактики на расстояние в 1000 км от наблюдателя с ускорением 3,5∙10–24 м/c2. Ускорение считать постоянным.
1. Какие величины являются количественными характеристиками гравитационного поля?
2. Сформулируйте закон всемирного тяготения.
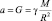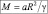