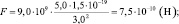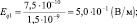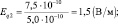Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.1.3. Электрическое поле
Электрическое поле характеризуется величиной, которую принято называть «напряжённость электрического поля» (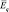
):
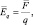(1.1.)
где 
– сила, воздействующая на пробный заряд q. Поскольку сила – величина векторная, то напряжённость – тоже векторная величина, являющаяся мерой силы, воздействующей на заряд (рис. 1.3). При использовании абсолютного значения силы (F) в уравнении (1.1.), частное будет представлять собой модуль напряжённости (Еq). Если источником электрического поля, воздействующего на заряд, является другой заряд, то F и 
будут определяться основным законом электростатики (законом Кулона), который гласит, что сила отталкивания двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению зарядов q1 и q2 и обратно пропорциональна квадрату расстояния r между ними:
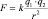– скалярная форма записи закона Кулона;
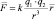– векторная форма записи закона Кулона,
где F – абсолютное значение силы отталкивания; k – коэффициент пропорциональности (k = 9∙109 Н∙м2/Кл2); r – расстояние между зарядами; 
– радиус-вектор, проведённый от источника электрического поля к точечному пробному электрическому заряду: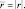 
Если заряд q1 воспринимается как источник электрического поля, тогда заряд q2 называется пробным зарядом, а напряжённость электрического поля (Еq1 и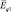 
) определяется равенствами:
– скалярная форма записи напряжённости электрического поля
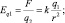(1.2)
– векторная форма записи напряжённости электрического поля
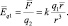(1.3)
Если в качестве источника электрического поля воспринимается заряд q2, то пробным зарядом является q1. В этом случае напряжённость электрического поля (Еq2 и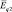 
) определяется равенствами:
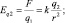
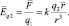
Согласно (1.2) модуль силы, действующей на пробный заряд (q2), можно представить произведением: F = q2∙Еq1, подобно тому как сила, воздействующая гравитационным полем Земли на массу m описывается равенством: Fm = mg. Развивая аналогию, можно утверждать, что подобно тому как потенциальная энергия взаимодействия (Wm) тела с Землей, поднятого над поверхностью на высоту h, определяется равенством: Wm = mgh, потенциальная энергия взаимодействия (W) пробного заряда q2 с источником электрического поля, удаленным от пробного заряда на расстояние r, рассчитывается по формуле:
W = q2Eq1r.
Так как q2∙Eq1 = F, то
W = F∙r.
Отношение W к величине пробного заряда называется потенциалом электростатического поля (φ)
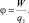
В системе СИ [φ] = Дж/Кл; 1 Дж/Кл ≡ 1 В (1 вольт).
Согласно (1.3) и последним двум равенствам
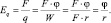(1.4)
А поскольку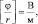 
то в системе СИ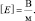 
Из (1.4) вытекает, что
φ = Еq∙r.
Потенциал, в отличие от напряжённости является скалярной величиной, характеризующей энергию электростатического поля. Разность потенциалов между двумя точками электростатического поля называется напряжением (U):
U = φ1 – φ2,
где φ1 – потенциал точки, расположенной на меньшем расстоянии от источника электрического поля по сравнению с точкой потенциала φ2. Напряжение, создаваемое в разных точках пространства зарядом q можно рассчитывать по формуле:
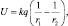
где r1 и r2 расстояния от различных точек пространства до заряда.
Действительно, обозначив через E′, W′, F′ соответственно напряжённость, потенциальную энергию и силу, создаваемую зарядом на расстоянии r1, а через E″, W″, F″ – на расстоянии r2, можем записать:
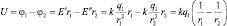
или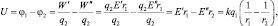 
или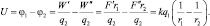 
Примеры решения задач
Задача 1
Во сколько раз сила отталкивания (Fo) превышает силу притяжения (Fп) двух протонов, обладающих массой по 1,67∙10–27 кг и зарядом по 1,60∙10–19 Кл.
|
Дано: q1 = q2 = 1,6∙10–19 Кл m1 = m2 = 1,67∙10–27 кг |
Решение
|
|
Fo /Fп – ? |
|
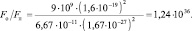
Ответ: сила отталкивания превышает силу притяжения в 1,24∙1036 раз (Fo /Fп = 1,24∙1036).
Задача 2
Рассчитать абсолютное значение (модуль) силы отталкивания двух точечных положительных зарядов, один из которых 0,5 нКл, а другой 1,5 нКл и находится на расстоянии 3,0 м от первого. Определить для этого расстояния:
– модуль напряжённости, создаваемый первым зарядом и модуль напряжённости, создаваемый вторым зарядом;
– координаты вектора напряжённости, создаваемого первым зарядом в точке (1; 2; 2) м;
– потенциальную энергию взаимодействия этих зарядов;
– потенциал электростатического поля, создаваемого вторым зарядом в точке нахождения первого заряда.
Вычислить напряжение, создаваемое первым зарядом, между точками, находящимися от него на расстоянии 2 см и 4 см.
|
Дано: q1 = 5,0∙10–10 Кл q2 = 1,5∙10–9 Кл r = 3,0 м
r1 = 2,0∙10–2 м r1 = 4,0∙10–2 м |
Решение:
W = F∙r; Подставив в полученные равенства значения величин, приведённых в «дано», получим: |
|
F – ? Eq1 – ? Еq2 – ?
W – ? φ – ? U – ? |
|
– ?
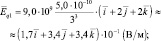
W = 7,5∙10–10∙3 = 2,25∙10–9 (Дж);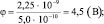 
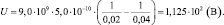
Ответ: F = 7,5∙10–10 Н; Еq1 = 5,0∙10–1 В/м; Еq2 = 1,5 В/м;
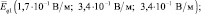
W = 2,25∙10–9 Дж; φ = 4,5 В; U = 1,125∙102 В
Задачи для самостоятельного решения
1. Рассчитать абсолютное значение силы отталкивания двух точечных положительных зарядов, один из которых 2 мкКл, а другой 3 мкКл и находится на расстоянии 3,7 м от первого. Определить для этого расстояния:
– модуль напряжённости, создаваемый первым зарядом и модуль напряжённости, создаваемый вторым зарядом;
– координаты вектора напряжённости, создаваемого вторым зарядом в точке (1; 2; 3) м;
– потенциальную энергию взаимодействия этих зарядов;
– потенциал электростатического поля, создаваемого первым зарядом в точке нахождения второго заряда.
Вычислить напряжение, создаваемое вторым зарядом, между точками, находящимися от него на расстоянии 4 мм и 8мм.
2. Определить величину зарядов, притягивающихся друг к другу на расстоянии 5 см с силой 705,6 Н, если известно, что модули этих зарядов равны.
1. Какой величиной характеризуется электрическое поле?
2. Сформулируйте закон Кулона.
3. Что такое напряжение и потенциал?
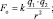
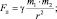
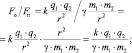
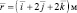
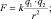
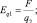
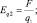
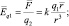
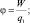
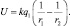
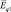