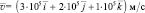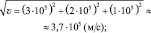Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.1.4. Магнитное поле
Магнитное поле характеризуется величиной  , которую принято называть «вектор магнитной индукции» (рис. 1.6).
, которую принято называть «вектор магнитной индукции» (рис. 1.6).
Вектор магнитной индукции – это условная мера силы, действующей на движущийся заряд.
Вектор магнитной индукции является псевдовекторной величиной, потому что в направлении, им обозначаемом, нет никакого движения или изменения. Однако, подобно тому как, зная температуру (Т) тела можно определить кинетическую энергию молекул (Ек), составляющих его[6] с помощью вектора магнитной индукции можно определить направление и величину силы, действующей на движущийся заряд. Направление силы определяется правилом левой руки:
«Если левую руку расположить так, чтобы четыре пальца ладони были направлены по движению положительно заряженной частицы, а вектор магнитной индукции входил в ладонь, то отставленный на 90° большой палец покажет направление действующей на частицу силы» (рис. 1.9).
Модуль этой силы (Fл), определяется равенством:
Fл = q∙v∙B∙sinα, (1.5)
где q, v, B – абсолютные значения заряда, скорости движения заряженной частицы, вектора магнитной индукции соответственно; α – минимальный положительный угол[7], образуемый векторами скорости и магнитной индукции. Сила, определяемая равенством (1.5) называется силой Лоренца. Согласно (1.5):
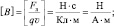

Математически правило левой руки записывается с помощью векторного произведения[8]:
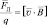
или 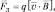
где q – алгебраическая[9] величина движущегося заряда.
Направление самого вектора магнитной индукции определяют правилом, которое называют правилом правого винта или правилом буравчика:
Если направление движения положительного заряда совпадает с направлением поступательного движения буравчика (правого винта), то направление вращения ручки буравчика (шляпки правого винта) совпадает с направлением вектора магнитной индукции (рис. 1.6). При этом, абсолютное значение вектора магнитной индукции, определяется формулой:
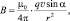
где μо = 4π∙10–7 Гн/м – магнитная постоянная (1 Гн ≡ 1 Тл∙м2/A); r – модуль радиус-вектора  , проведённого из движущегося заряда, в рассматриваемую точку поля; v – абсолютное значение вектора скорости движения; α – угол между векторами
, проведённого из движущегося заряда, в рассматриваемую точку поля; v – абсолютное значение вектора скорости движения; α – угол между векторами  и
и  . Вместо правила буравчика можно использовать строгую математическую запись:
. Вместо правила буравчика можно использовать строгую математическую запись:
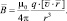
Наряду с понятием «вектор магнитной индукции» нередко используют в расчётах такую величину, как «напряжённость магнитного поля» (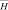 ),
),
которая для условий вакуума вычисляется по следующим уравнениям:
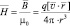
или 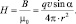
Линия, касательные к которой в любой точке являются вектором магнитной индукции называется магнитной линией. С помощью магнитных линий рис. 1.6 можно преобразовать в рис. 1.10.
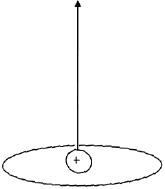
Рис. 1.10 Магнитные линии, создаваемые движущимся зарядом
Следует отметить, что хотя магнитное поле является вихревым, однако, если траектория движения потока заряженных частиц представляет собой спираль с большим количеством колец, плотно прижатых друг к другу (соленоид), то внутри этой спирали магнитное поле можно считать практически однородным. То есть вектор магнитной индукции одинаков по направлению и по модулю внутри соленоида, на протяжении всей его длины (рис. 1.11).
Стрелки на спирали символизируют направление движения положительно заряженных частиц. Стрелки, выходящие из соленоида и входящие в соленоид символизируют направление вектора магнитной индукции. Именно этим и обусловлены свойства магнитов, внутри которых непрерывно текут одинаково ориентированные замкнутые токи электронов (рис. 1.12).
При этом не следует забывать, что поскольку электроны являются отрицательно заряженными частицами, то на самом деле они движутся в направлении противоположном тому, которое считается направлением движения заряженных частиц и указанному на рис. 1.11, 1.12.

Рис. 1.12. Схема строения магнита
Примеры решения задач
Задача 1
Определить координаты и модуль силы Лоренца, воздействующей на движущийся точечный заряд 2 нКл, вектор скорости которого имеет координаты (3∙107; 2∙107; 1∙107) м/c, а координаты вектора магнитно й индукции (0,1; 0,2; 0,3) Tл.
|
Дано: q = 2∙10–9 Кл;
|
Решение
|
|
Fл – ? |
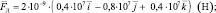
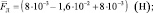
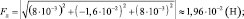
Ответ: 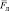 (8∙10–3 Н; –1,6∙10–2 Н; 8∙10–3 Н); Fл ≈ 1,96∙10–2 Н.
(8∙10–3 Н; –1,6∙10–2 Н; 8∙10–3 Н); Fл ≈ 1,96∙10–2 Н.
Задача 2
Рассчитать координаты и модуль силы Лоренца, воздействующей на движущийся точечный заряд 2 нКл, вектор скорости которого имеет координаты (3∙107; 2∙107; 1∙107) м/c, а координаты вектора магнитной индукции (0,15; 0,10; 0,05) Тл. Чему равен угол между направлениями вектора магнитной индукции и вектора скорости движения заряженной частицы?
|
Дано: q = 2 нКл;
|
Решение
Выполняя действия, аналогичные действиям предыдущей задачи, получим:
Следовательно:
|
|
Fл – ? α – ? |
Fл = 0 (Н).
Нулевое значение силы Лоренца свидетельствует о том, что sin α = 0, то есть, векторы  и
и  коллинеарны – лежат на одной прямой. Поскольку, значения координат обоих векторов больше 0, то эти коллинеарные векторы равнонаправлены, то есть α = 0.
коллинеарны – лежат на одной прямой. Поскольку, значения координат обоих векторов больше 0, то эти коллинеарные векторы равнонаправлены, то есть α = 0.
Ответ: Fл (0 Н; 0 Н; 0 Н); Fл = 0 Н; α = 0.
Задача 3
Для точки с координатами (1; 1; 1) м рассчитать координаты и модуль вектора магнитной индукции, создаваемого зарядом 0,1 мкКл, движущимся со скоростью, координаты которой (3∙105; 2∙105; 1∙105) м/c.
|
Дано: q = 1∙10–7 Кл
|
Решение
Поскольку
|
|
B – ? |
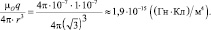
Поэтому:
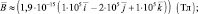
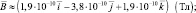
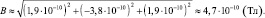
Ответ:  (1,9∙10–10 Тл; – 3,8∙10–10 Тл; 1,9∙10–10 Тл); В ≈ 4,7∙10–10 Тл.
(1,9∙10–10 Тл; – 3,8∙10–10 Тл; 1,9∙10–10 Тл); В ≈ 4,7∙10–10 Тл.
Задача 4
Какова длина радиус-вектора, проведённого от заряда, рассмотренного в предыдущей задаче, к точке, в которой абсолютное значение вектора магнитной индукции составляет 4,6 мТл, если этот радиус-вектор перпендикулярен направлению движения заряда?
|
Дано: q = 1∙10–7 Кл
B = 4,6∙10–3 Тл α = 90° |
Решение
|
|
r – ? |
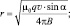
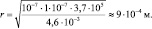
Ответ: r ≈ 9∙10–4 м
Задачи для самостоятельного решения
1. Определить направление (северное, южное, западное, восточное) и абсолютное значение силы Лоренца, действующей на электрон (–1,6∙10–10 нКл), движущийся в вакууме с севера на юг со скоростью 3∙103 км/c в магнитном поле с напряжённостью 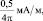 направленном на электрон снизу под углом к вектору скорости его движения, составляющим:
направленном на электрон снизу под углом к вектору скорости его движения, составляющим:
а) 90°
б) 45°
в) 30°
2. Определить направление (северное, южное, западное, восточное) и абсолютное значение вектора магнитной индукции, создаваемого протоном (1,6∙10–10 нКл), движущимся со скоростью 3∙103 км/c сверху вниз, в точке,
а) расположенной западнее протона на расстоянии r = 3 см от него и образующей с протоном радиус-вектор, составляющий с вектором движения протона плоский угол β1 = 90°;
б)) расположенной в плоскости угла β1, но образующей с протоном радиус-вектор, составляющий с вектором движения протона угол β2 = 45°;
в) β3 = 30°;
г) β4 = 0°;
д) β5 = 150°.
3. Определить координаты и модуль силы Лоренца, воздействующей на движущийся точечный заряд 1∙10–7 Кл, вектор скорости которого имеет координаты (2∙106; 1∙105; 3∙105) м/c, а координаты вектора магнитной индукции (0,1; –0,2; 0,1) Тл.
4. Определить координаты и модуль силы Лоренца, воздействующей на движущийся точечный заряд 0,5∙10–8 Кл, вектор скорости которого имеет координаты (6∙105; –4∙105; 8∙105) м/c, а координаты вектора магнитной индукции (–0,3; 0,2; –0,4) Тл. Чему равен угол α между направлениями вектора магнитной индукции и вектора скорости движения заряженной частицы?
5. Для точки (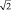 ; 1; 1) м определить координаты и модуль вектора магнитной индукции, создаваемой зарядом 0,3 мкКл, движущимся со скоростью, координаты которой (1∙104; 1∙104; 1∙105) км/c.
; 1; 1) м определить координаты и модуль вектора магнитной индукции, создаваемой зарядом 0,3 мкКл, движущимся со скоростью, координаты которой (1∙104; 1∙104; 1∙105) км/c.
6. Какова длина радиус-вектора, проведённого от заряда, рассмотренного в предыдущей задаче, к точке, в которой абсолютное значение вектора магнитной индукции составляет 3 мТл, если этот радиус-вектор перпендикулярен направлению движения заряда?
1. Какой величиной характеризуется магнитное поле?
2. Сформулируйте правило левой руки и правило правого винта (буравчика).
3. Почему соленоиды проявляют свойства магнитов?

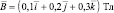
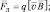
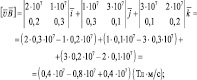
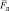 – ?
– ?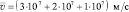
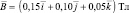
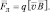
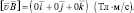
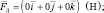
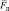 – ?
– ?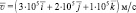
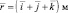
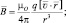
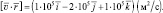
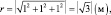 то
то – ?
– ?