Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.1.5. Вращение заряженной частицы в потоке магнитной индукции
Ускорение заряженной частицы под действием силы Лоренца нормальное (
), то есть, направлено перпендикулярно скорости её движения, а значит, изменяет направление движения частицы, но не изменяет значения модуля скорости её движения. Это приводит к тому, что заряженная частица, движущаяся в постоянном магнитном поле начинает вращаться по окружности с радиусом r. Нормальное ускорение определяется формулами:
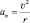– скалярная форма уравнения;
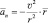– векторная форма уравнения,
где 
– радиус-вектор, проведённый из центра окружности в точку движения – абсолютное значение скорости.
Согласно второму закону Ньютона (F = ma или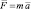 
):
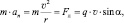
где q, v, B – абсолютные значения заряда, скорости движения заряженной частицы, вектора магнитной индукции соответственно; α – угол, образуемый векторами скорости и магнитной индукции.
Или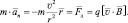 
Из двух последних выражений следует, что
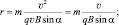(1.6)
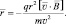(1.7)
То есть, заряженная частица с массой m и зарядом q, движущаяся со скоростью 
в постоянном магнитном поле, обладающем вектором магнитной индукции В, будет вращаться по окружности с радиусом, определяемым формулой (1.6). Направление движения вращающейся частицы, естественно, всё время меняется, поэтому и направление соответствующего радиус-вектора также непрерывно меняется и определяется равенством (1.7).
Примеры решения задач
Задача 1
Определить радиус окружности, по которой со скоростью 3 м/c вращается заряженная частица 2 мкКл массой 0,1 мг, находящаяся в магнитном поле, вектор магнитной индукции которого перпендикулярен направлению движения этой частицы и составляет 0,4 Тл.
|
Дано: v = 3 м/c q = 2∙10–6 Кл m = 1∙10–7 кг B = 0,4 Тл |
Решение На основании (1.6) можем записать
Поскольку по условию задачи вектор магнитной индукции перпендикулярен направлению движения заряженной частицы, то sin α = 1. Поэтому в данном случае |
|
r – ? |
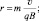
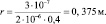
Ответ: r = 0, 375 м.
Задача 2
Установить координаты радиус-вектора заряда 5 мкКл, вращающегося в магнитном поле по окружности радиусом 0,5 м и обладающего массой 0,3 мг, для момента времени, при котором координаты скорости приобрели значения (1; 2; 3) м/с. При этом 
(0,3; 0,2; 0,1) Тл.
|
Дано: q = 5∙10–6 Кл r = 5∙10–1 м m = 3∙10–7 кг
|
Решение На основании (1.7) можем записать
Поскольку v2 = 12 + 22 + 32 = 14 (м2/c2), то
|
|
|
– ?Поэтому:
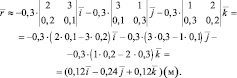
Ответ: 
(0,12 м; –0,24 м; 0,12 м).
Задачи для самостоятельного решения
1. Определить массу заряда 0,4 мкКл, вращающегося со скоростью 5 м/c по окружности диаметром 0,1 м, которая перпендикулярна магнитному полю с В = 0,4 Тл.
2. Установить координаты радиус-вектора заряда 0,3 мкКл, вращающегося в магнитном поле по окружности радиусом 0,7 м и обладающего массой 0,9 мг, для момента времени, при котором координаты скорости приобрели значения (3; 1; 2) м/с.
При этом 
(0,5; 0,7; 0,9) Тл.
Почему заряженная частица, движущаяся в постоянном магнитном поле, вращается по окружности?
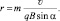
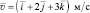
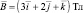
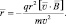
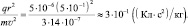