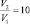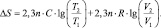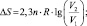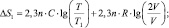Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.1.9. Элементы термодинамики
Термодинамика – это раздел физики, изучающий закономерности движения теплоты и внутренней энергии макроскопических тел.
Физические системы, в которых рассматриваются закономерности движения теплоты и внутренней энергии макроскопических тел называются термодинамическими системами. В известном уравнении состояния идеального газа Менделеева – Клапейрона:
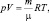
где p – давление; V – объём; m – масса; μ – молярная масса; R – универсальная газовая постоянная (R ≈ 8,31 Дж/(моль∙К); Т – абсолютная температура, произведение pV имеет размерность энергии. Однако, реальные газы, помимо энергии, определяемой произведением pV, обладают целым набором других видов энергии:
– энергией массы каждой молекулы (Е0 = mc2);
– кинетической энергией молекул (Ек = mv2/2);
– потенциальной энергией взаимодействия молекул (Еп);
– энергией ядерного взаимодействия между нуклонами атомов (ЕЯ);
– энергией взаимодействия между электронами и ядрами (ЕЭ) и т. д.
Их совокупность называют внутренней энергией (U).
Сумму U + pV называют энтальпией и, как правило, обозначают буквой Н:
Н = U + pV. (1.11)
Для жидких и твёрдых веществ Н = U.
Энтропия
Согласно первому закону термодинамики:
Изменение внутренней энергии системы (U) при переходе её из одного состояния в другое равно сумме работы внешних сил (А) и количества теплоты (Q), переданного системе:
∆U = А + ∆Q.
Если внешние силы никакой работы не совершают, то
∆U = ∆Q.
При этом, как известно:
∆Q = cm (T2 – T1) = ∆Tcm,
где с – удельная теплоёмкость системы; m – масса; T1 – первоначальная температура; T2 – конечная температура. Поскольку температура T идеального газа пропорциональна средней кинетической энергии (Ек) его молекул:
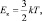
где k – постоянная Больцмана (k = 1,38∙10–23 Дж/К), то можно утверждать, что внутренняя энергия увеличивается за счёт превращения подводимого тепла в кинетическую энергию молекул.
Если наоборот, вся подводимая теплота расходуется на преодоление внешних сил, которые при этом, совершают отрицательную работу (например, при расширении газа с неизменной температурой в воздушном шаре под лучами солнца):
∆Q = –А,
то внутренняя энергия системы при этом не изменится:
∆U = 0,
но, тем не менее, состояние системы станет другим. Молекулы газа после его расширения получат возможность более свободно перемещаться в пространстве – возрастёт беспорядок их движения. При этом часть энергии газа потеряет возможность производить работу (обесценится), так как некоторая работа по расширению газа окажется уже произведённой. В этом случае говорят, что возросла ЭНТРОПИЯ (S) газа, являющаяся мерой его беспорядка и обесцененной энергии. Количественное изменение этой энтропии (∆S) определяется отношением подведённого количества теплоты (∆QЭ) к абсолютной температуре:
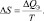 (1.12)
(1.12)
Таким образом, [S] = Дж/К.
Для абсолютного значения энтропии:
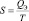 .
.
При этом величину QЭ называют энтропийной энергией:
QЭ = T∙S.
Другим примером возрастания энтропии и энтропийной энергии при постоянной температуре может служить превращение воды в пар при 100 °С. Или превращение льда в жидкость при температуре 0 °С.
Изменение температуры любой системы также приводит к изменению энтропии. Для идеального газа зависимость изменения энтропии от изменения температуры и объёма выглядит следующим образом:
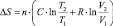 (1.13)
(1.13)
или в дифференциальной форме:
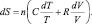
Энергия Гельмгольца и энергия Гиббса
Внутреннюю энергию (U) иногда делят на две части:
U = F + TS, (1.14)
где TS – энтропийная энергия; F – сумма всех остальных составляющих внутренней энергии, которая называется энергией Гельмгольца.
На основании (1.11) и (1.14) энтальпию (Н) можно представить суммой трёх составляющих:
H = F + TS + pV.
Если ввести обозначение
F + pV = G, то H = G + TS,
где величина G называется свободной энергией или энергией Гиббса
G = H – TS.
Для изотермических процессов:
∆G = ∆H – T∆S.
Критерии возможности самопроизвольного протекания процесса
Согласно одной из формулировок второго закона термодинамики: энтропия замкнутой системы[10], при любых происходящих в ней процессах не убывает[11]:
∆S ≥ 0.
Если процесс необратим[12], то ∆S > 0, если обратим[13], то ∆S = 0.
Таким образом, критерием возможности протекания процесса в замкнутой системе может служить знак изменения энтропии. Процесс возможен только в том случае, если знак изменения энтропии неотрицателен.
Действительно, трудно представить себе систему, в которой происходило бы упорядочение без обмена энергией с внешней средой. Например, перемешивание двух различных газов приводит к возрастанию беспорядка (энтропии), значит, такой процесс самопроизвольно протекать может. Обратный же процесс разделение перемешанных газов означает упорядочение, то есть, уменьшение энтропии, следовательно, такой процесс самопроизвольно протекать не может. Однако в открытых (незамкнутых) системах энтропия может убывать. Например, вода при 0 °С, отдавая свою внутреннюю энергию внешней среде, превращается в лёд. Критерием возможности протекания процесса в незамкнутой системе может служить знак изменения энергии Гиббса. Процесс в незамкнутой системе возможен только в том случае, если знак изменения энергии Гиббса неположителен:
∆G ≤ 0,
то есть
∆Н – Т∆S ≤ 0,
если ∆G < 0, процесс необратим, если ∆G = 0 процесс обратим. Например, для процесса замерзания воды при 0 °С справедливо равенство Н = Т∆S, то есть уменьшение внутренней энергии системы равно уменьшению её энтропийной энергии. Выделяющееся тепло представляет собой исключительно энергию упорядочения молекул воды в структуру льда.
∆Н – Т∆S = 0;
∆G = 0.
Это значит, что скорости процессов замерзания воды и таяния образующегося льда в этих условиях равны друг другу за счет того, что выделяющееся при кристаллизации тепло опять расходуется на плавление.
Согласно одной из формулировок третьего закона термодинамики: при абсолютном нуле температуры энтропия равна нулю[14].
То есть, при Т = 0 К, S = 0.
Следует подчеркнуть условность приведённой формулировки. На самом деле оценить значение энтропии при 0 °К невозможно в принципе. Однако было доказано, что при абсолютном нуле изотермические процессы протекают без изменения энтропии. Таким образом, значение энтропии любой системы при 0 °К наименьшее, относительно которого можно измерять все изменения этой величины. Хотя и условно, но практически очень удобно, это наименьшее значение энтропии считать равным нулю.
Примеры решения задач
Задача 1
Определить на сколько изменится энтропия и энтропийная энергия одного моля идеального газа если его объём увеличить в 10 раз при постоянной температуре равной 25 °С?
|
Дано: n = 1 моль
|
Решение
Поскольку T2 = T1, то ∆S = 2,3∙1∙8,31∙lg 10 ≈ 19,1 Дж/К; |
|
∆S – ? ∆QЭ – ? |
∆QЭ = Т∆S;
∆QЭ = 298∙19,1 = 5691,8 Дж.
Ответ: ∆S ≈ 19,1 Дж/К; ∆QЭ ≈ 5,7 кДж.
Задача 2
Оценить на сколько изменится энтропия замкнутой системы, состоящей из двух одинаковых объёмов водорода с температурой 7 °С и 57 °С, содержащих по 2 грамма газа, если после перемешивания температура общего объёма составила 32 °С. Молярную теплоёмкость водорода считать равной 20,8 Дж/моль∙K и независимой от температуры.
|
Дано: m = 2 г ≡ 2∙10–3 кг Т1 = 7 °С ≡ 280 K V Т2 = 57 °С ≡ 330 K Т = 32 °С ≡ 305 K C = 20,8 Дж/моль∙K М = 2∙10–3 кг/моль |
Решение В данном случае общее возрастание энтропии обусловлено изменением энтропии двух составляющих системы, равные объёмы V каждой из которых удваиваются, то есть становятся равными 2. ∆S = ∆S1 + ∆S2;
|
|
∆S – ? |
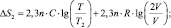
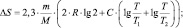
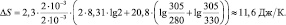
Ответ: ∆S ≈ 11,6 Дж/К.
Задачи для самостоятельного решения
Задача
1. Замкнутая система состоит из двух идеальных газов, разделенных перегородкой (рис. 1. 18).
Рис. 1.18. Газы, разделённые перегородкой
Первый газ в количестве 2 моль занимает объём 3 м3, а второй газ в количестве 3 моль занимает объём 2 м3. На сколько изменится энтропия системы после удаления перегородки? На сколько изменится энтропийная энергия, если процесс перемешивания газов проводить при 25 °С?
2. Определить количество газа занимающего при 25 °С объём 3 л и оказывающего на стенки занимаемого им сосуда давление 105 Па?
1. Сформулируйте три закона термодинамики.
2. Дайте определения следующих понятий: внутренняя энергия, энтальпия, энтропия, энтропийная энергия, энергия Гельмгольца, энергия Гиббса.
3. Каковы критерии возможности самопроизвольного протекания процесса для замкнутых и открытых систем?