Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.2.8. Специальная теория относительности
Для СТО А. Эйнштейн сформулировал два постулата:
1. Все процессы природы протекают одинаково во всех инерциальных системах отсчёта.
2. Скорость света в вакууме одинакова для всех инерциальных систем отсчёта. Она не зависит ни от скорости источника, ни от скорости приёмника светового сигнала.
Кроме того, были разделены понятия «время» и «интервал времени». Поэтому и мы, в рамках СТО под временем t будем подразумевать показания синхронизированных часов в конкретный момент, а интервал времени Δt, пусть, означает расстояние, преодолеваемое концом минутной (часовой, секундной) стрелки, измеряемое в минутах (часах, секундах). Например, взглянув на различные часы с одинаковыми положениями стрелок (синхронизированные), мы фиксируем время. А, заметив расстояние, которое пройдёт свободный конец минутной стрелки в течение 10 минут, мы фиксируем интервал времени, равный 10 минут (Δt = 10 минут).
Опираясь на приведённые постулаты и математические преобразования координат в движущихся системах отсчёта, разработанные Х.А. Лоренцем, А. Эйнштейн пришёл к выводу о несовпадении течения времени в движущемся и покоящемся объектах (системах отсчёта). Например, если космический корабль (S) движется относительно неподвижной космической станции (S0) со скоростью v, то:
(1.15)
где t0 – время, фиксируемое наблюдателем в неподвижной станции по своим часам (часам станции S0); t – время, фиксируемое тем же
наблюдателем по синхронизированным часам космического корабля S; х0 – расстояния между станцией и кораблём, наблюдаемой со станции; с – скорость света. Как видно из уравнения, соотношение между t0 и t в рассматриваемых объектах зависит не только от скорости их движения v относительно друг друга, но и от расстояния между ними. Причём, соотношение между расстоянием х0 и этим же расстоянием, но наблюдаемым из движущегося объекта (х), выглядит следующим образом:
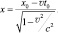(1.16)
Если в уравнении (1.15) расстояние х0 представить тождеством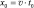 
, то можно получить равенство:
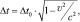(1.17)
где Δt0 – интервал времени, наблюдаемый неподвижным наблюдателем по часам неподвижной системы; Δt – тем же наблюдателем по часам движущейся системы. Из 27.3 следует, что неподвижный наблюдатель увидит замедление течения времени в движущемся объекте.
Подставив в уравнение (1.15) значение х0 из выражения (1.16) получим, что при t0 = 0 (в полночь на космической станции) часы на удаляющемся от станции космическом корабле будут восприниматься наблюдателем космической станции как отстающие:
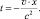
То есть, отставание часов на космическом корабле будет наблюдаться не только из-за медленного в нём течения времени, но также из-за удаленности космического корабля от станции. Более того, часы синхронизированные и расположенные в противоположных концах космического корабля будут восприниматься наблюдателем с неподвижной станции как рассинхронизированные, т. е., показывающие разное время, поскольку будут находиться на разном расстоянии от наблюдателя. Такое явление получило название «Относительность одновременности». Действительно, для членов экипажа удаляющегося космического корабля все их синхронизированные часы показывают одно и то же время одновременно, а для наблюдателей из космической станции – чем дальше часы по направлению движения, тем сильнее они отстают от часов станции. Причём, если космический корабль приближается к станции, то наблюдатель станции будет воспринимать часы космического корабля спешащими вперёд (рис. 1.27)
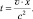
Рис. 1.27. Схема отклонения синхронизированных часов:
1 – стрелка часов неподвижной космической станции;
2 – стрелка часов космического корабля, удаляющегося от станции;
3 – стрелка часов космического корабля, приближающегося к космической станции
Важной частью СТО стал также вывод об уменьшении размеров тел вдоль направления их движения:
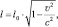(1.18)
где l0 – длина неподвижного тела; l – длина этого же тела, движущегося со скоростью v, относительно неподвижного наблюдателя в направлении измеряемой длины.
Интересно отметить, что последнее уравнение математически совпадает с уравнением (1.17), хотя физический смысл его совсем иной.
Помимо сказанного, А. Эйнштейн сформулировал закон сложения скоростей, близких к скорости света, согласно которому:
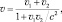
где v1 – скорость движения объекта относительно неподвижного наблюдателя (например, скорость космического корабля относительно космической станции) (рис. 1.28); v2 – скорость движения другого объекта (например, другого космического корабля) относительно того же наблюдателя; v – скорость движения этих объектов относительно друг друга.
Если v1 << с и v2 << с, то v = v1 + v2. То есть, закон сложения скоростей, применяемый в механике Ньютона, оказывается частным случаем более общего закона сложения скоростей специальной теории относительности. Уравнение сложения скоростей специальной теории относительности превращается в уравнение сложения скоростей механики Ньютона при скоростях намного меньше скорости света. Причём этот вывод оказался справедливым по отношению ко многим уравнениям СТО. Действительно, при v << с уравнение (1.18) превращается в равенство l = l0, уравнение (1.17) в тождество Δt = Δt0, уравнение (1.15) в равенство t = t0.
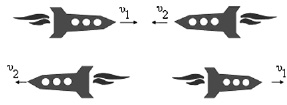
Рис. 1.28. Иллюстрация закона сложения скоростей объектов,
движущихся в противоположных направлениях
В рамках СТО А. Эйнштейн вывел также уравнение, устанавливающие зависимость между массой (m) и энергией (E), заключённой в ней:
E = mc2.
И, всё-таки, наиболее парадоксальным выводом СТО до сих пор считается относительность времени, описываемая уравнением (27.3).
При этом, поскольку время оказалось относительным, то все события в рамках рассматриваемой теории рассматриваются не относительно времени, а относительно инвариантного интервала s, определяемого по формулам:
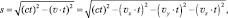
где vх, vy, vz – проекции скорости v на координатные оси x, y, z. Соответственно:
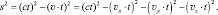(1.19)
Таким образом, все события в СТО измеряются относительно параметра, представляющего собой функцию трёх пространственных координат и времени. То есть, пространство и время рассматриваются как аспекты единого четырёхмерного пространства (континуума), в котором величина сt является четвёртой координатой.
В привычном для нас трёхмерном пространстве Эвклида квадрат длины интервала, преодолеваемого любым объектом, представляет собой сумму квадратов проекций этой длины на координатные оси (сумму квадратов координат):
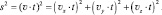
Аналогично рассчитывается квадрат длины для четырёх и более мерного пространства Эвклида – как сумма квадратов всех координат:
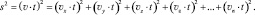
Однако, в СТО, квадрат длины четырёхмерного пространственно-временного континуума представляет собой разницу между квадратом координаты ct и квадратом трёх оставшихся пространственных координатам (уравнение (1.19)). Такое пространство, в отличие от пространства Эвклида, принято называть пространством Минковского. Но поскольку многие сложные уравнения четырёхмерного пространственно-временного континуума могут преобразовываться в привычные уравнения трёхмерного Эвклидова пространства, то в дальнейшем мы будем рассматривать именно последние.
Общепризнанная теория СТО, на самом деле привела к парадоксу, получившему название «Парадокс близнецов». Суть его состоит в том, что течение времени в движущемся объекте должно замедляться и все события, протекающие на нём, восприниматься, как в замедленном фрагменте фильма. Получается, что человек, оставшийся на Земле, может встретить через много лет своего брата-близнеца, летавшего на космическом корабле с около световыми скоростями, значительно моложе себя. Потому что время в таком космическом корабле текло медленнее. Однако, с около световой скоростью летит не только космический корабль относительно Земли, но и наоборот – Земля относительно космического корабля также движется с той же скоростью! А это значит, что космонавт должен воспринимать процессы, протекающие на Земле… подобно замедленному фрагменту фильма точно также как и наблюдатель с Земли, который будет видеть события на космическом корабле замедленными! Тогда кто же из близнецов окажется младше – оставшийся на Земле или вернувшийся из космического путешествия? Окончательное разрешение этот парадокс получил уже в рамках общей теории относительности.