Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Естествознание постнеклассической науки

Шепель О. М.,

§ 1.2.9. Общая теория относительности

Согласно ОТО течение времени замедляется во всех неинерциальных системах, т. е. движущихся с ускорением или находящихся в гравитационном поле.

Например, в гравитационном поле:

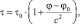
где τ – интервал времени, наблюдаемый в гравитационном поле с Ньютоновским гравитационным потенциалом φ (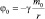 см. § 7); τ0 – интервал времени, наблюдаемый в гравитационном поле с Ньютоновским гравитационным потенциалом φ0 .

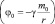А в космическом корабле, движущемся равноускоренно или равнозамедленно, с абсолютным значением собственного ускорения, равным а:

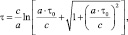
где τ0 – интервал времени ускорения, измеренный в неподвижной системе отсчёта; τ – интервал времени ускорения, измеренный в космическом корабле.

При этом следует подчеркнуть, что если равномерное движение инерциальных систем является относительным – т. е. после перемещения наблюдателя из покоящейся системы в движущуюся, последняя становится покоящейся, а покоящаяся воспринимается как движущаяся – то ускоренное или замедленное движение абсолютно! Это значит, что даже после перемещения наблюдателя из покоящейся системы в неинерциальную, движущуюся с ускорением (замедлением), последняя всё равно останется движущейся с ускорением (замедлением). Принципиальным отличием ускоряющихся (замедляющихся) систем является наличие воздействующей на них силы – система не может ускоряться или замедляться без воздействия внешней силы. Если неподвижный наблюдатель будет видеть замедление времени в такой неинерциальной системе, то наблюдатель из этой неинерциальной системы будет воспринимать ускорение времени у неподвижной системы. Анализ последнего уравнения показывает, что действительно τ < τ0. Следовательно космический путешественник, летящий на сперва ускоряющемся, а потом замедляющемся звездолёте вернётся на землю более молодым, чем состарившийся на Земле его брат-близнец.

Согласно ОТО, за время разгона космический корабль приобретает скорость v, определяемую по уравнению:

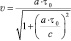(1.20)

и преодолевает расстояние х, рассчитываемое по формуле:

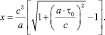
На участках равномерного полёта в течение времени τ′, когда космический корабль опять становится инерциальной системой, замедление времени описывается уравнениями СТО. При этом, если полагать, что до этого звездолёт ускорялся с постоянным ускорением (а) в течение времени τ0, то после подстановки уравнения (1.20) в равенство (1.15) получим выражение:

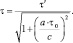(1.21)

Таким образом, космический путешественник вернётся домой более молодым, чем его брат-близнец, оставшийся на Земле, однако, не потому, что летал с очень большими, около световыми скоростями, а из-за ускорений, необходимых для достижения таких скоростей и замедлений, неизбежных при посадках на других планетах и возвращении на Землю.

Кроме того, согласно ОТО гравитационные взаимодействия масс, вызывающие их ускоренное движение по отношению друг к другу суть проявление искривления четырёхмерного пространства Минковского.

Фотон в таком пространстве постоянно меняет своё направление по отношению к направлению первоначальному. Чем больше масса, тем сильнее возле неё пространственная кривизна, воспринимаемая нами как тяготение. Например, луч света далёкой звезды, проходя рядом с солнцем – самым мощным источником гравитационного поля солнечной системы – отклоняется от своего направления на угол, достаточно значительный, чтобы быть измеренным земными наблюдателями (рис. 1.29).

Кроме того, искривление пространства вблизи Солнца приводит к заметной прецессии траектории вращения Меркурия (рис. 1.30) вокруг нашей звезды (отклонению от первоначальной окружности).

Рис. 1.29. Отклонение направления от прямой луча звезды, проходящего возле Солнца

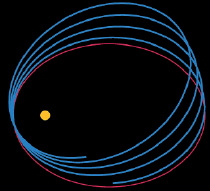
Рис. 1.30. Орбита по Ньютону (красная)
и по Эйнштейну (синие) Мекурия, вращающегося вокруг Солнца

Искривлённый четырёхмерный пространственно-временной континуум называется пространством Римана.

То есть, А. Эйнштейн показал, что свойства гравитационного поля являются свойствами кривизны пространственно-временного континуума. Им было теоретически предсказано, а, затем другими исследователями экспериментально подтверждено, что:

1. Пространство обладает определённой геометрической структурой (в данном случае кривизной)

2. Свойства гравитационного поля являются результатом структурирования (искривления) пространства массой.

Именно факт взаимодействия массы и пространства позволил утверждать возможность существования объект-пространственного взаимодействия (рис. 1.19, стр. 48).

При этом уравнения ОТО переходили в уравнения СТО если пространственно-временной континуум рассматривался как линейная протяжённость. СТО оказалась частным случаем ОТО, реализуемым при искривлённости равной нулю.

В этой ситуации естественно было предположить, что свойства электрического и магнитного полей также являются результатом какого-то структурирования пространства, возможно, более сложного. Нахождение строгого доказательства этого предположения А. Эйнштейн считал ближайшей программой минимум для современной ему физики. Однако, не было предела научной дерзости Великого учёного. Создатель специальной и общей теории относительности мечтал также открыть законы, которые объясняли бы все свойства всех элементарных частиц геометрическими свойствами пространства. Эту задачу он считал программой максимум. Теория, которая позволяла бы решить программу минимум и программу максимум, будучи даже не созданной, получила название «ЕДИНАЯ ТЕОРИЯ ПОЛЯ (ЕТП)». При этом, ОТО стала бы частным случаем, фрагментом ЕТП. Ещё при жизни выдающегося физика, после открытия ядерных взаимодействий (сильных и слабых), создание теории единого поля было существенно осложнено, поскольку новые взаимодействия также следовало объяснять в рамках разрабатываемой теории. Открытие запутанных частиц, взаимодействующих мгновенно, выявило границы применимости постулата ОТО об ограниченности скорости любого взаимодействия скоростью света, так как для запутанных частиц этот постулат оказался неприменим. Свойства запутанных частиц объясненяются только в рамках квантовой теории поля, упомянутой в §  1.2.6
и объясняющей свойства гравитационного поля взаимным обменом гипотетическим гравитонами между элементарными частицами. Удастся ли когда-нибудь объеденить общую теорию относительности и квантовую теорию поля? Это предстоит решать будущим поколения исследователей. Возможно, что именно Вам!

Задачи для самостоятельного решения

1. С какой скоростью относительно друг друга движутся два фотона, летящие в противоположных направлениях?

2. С какой скоростью в противоположных направлениях движутся два объекта относительно друг друга если скорость одного из них равна с, а другого с/n, где n ≥ 1?

3. Скорость течения реки относительно неподвижного острова составляет v, м/c. Определить скорость движения фотона, летящего в направлении течения реки, относительно самой реки и относительно острова.

4. Космический корабль пролетает мимо неподвижной орбитальной станции со скоростью 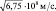Тело командира корабля ориентировано вдоль направления полёта. Определить рост командира космического корабля относительно орбитальной станции, если для экипажа космического корабля рост командира 180 см.

5. Оценить энергию массы своего тела. Выразить её в Дж и кДж.

6. Два космических корабля летят навстречу друг другу. Абсолютное значение скорости одного из них 200 000 км/c, другого 230 000 км/c. Каково абсолютное значение скорости кораблей относительно друг друга?

7. На сколько микросекунд уходят вперёд часы за сутки на космическом корабле GPS-навигации (Global Positioning System – система глобального позиционирования) по отношению к Земным часам (τ1 – τ0 = Δτ1) из-за меньшего гравитационного поля, и на сколько микросекунд они отстают из-за высокой скорости движения корабля (τ2 – τ0 = Δτ2), если он вращается вокруг Земли на высоте 20 200 км над уровнем моря с линейной скоростью 1,3 км/c. На сколько микросекунд, в конечном итоге, изменится время на космическом корабле за сутки (Δτ1 + Δτ2 = Δτ)? Масса Земли 6,0∙1024 кг, средний радиус Земли 6 371 км, гравитационная постоянная 6,67∙10–11 Н∙м2/кг2.

8. Космический корабль летит к звёздной системе Альфа Центавра, удалённой от Земли на расстояние х в 4,3 световых года (св. года). Первую половину пути корабль разгоняется с ускорением а равным 1 св. год/год2, вторую половину пути тормозит с тем же ускорением. Скорость света в данных единицах измерения 1 св. год/год. Равномерного полёта с постоянной скоростью нет (τ′ = 0). Затем корабль разворачивается и повторяет этапы разгона и торможения. Рассчитать:

– время, которое в течение этого полёта пройдёт на Земле (τ0);

– время, которое в течение этого полёта пройдёт на космическом корабле (t);

– максимальную скорость, которую достигнет космический корабль (v);

– значение ускорения космического корабля в системе СИ.

9. Рассчитать те же параметры, для того же космического корабля, двигающегося в том же режиме, но по направлению к Галактике Андромеды, удалённой от Земли на 2,5 миллиона световых лет.

10. Космический корабль отделился от неподвижной космической станции и удаляется от неё, набрав скорость 36 000 км/c. Определить разницу в показаниях синхронизированных на корабле часов, наблюдаемых с космической станции и находящихся друг от друга относительно неподвижного наблюдателя на расстоянии 500 м по направлению движения корабля.

1. В чём состоит особенность подхода А. Эйнштейна к рассмотрению пространства и времени? Каковы постулаты его специальной теории относительности?

2. Какую связь устанавливает общая теория относительности между гравитационным полем и геометрическими свойствами пространства?