Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Предельные теоремы теории вероятностей: учебное пособие

Селиверстова И. Ф.,

1.2. Неравенство (лемма) Маркова

Если случайная величина X не принимает отрицательных значений, то для любого положительного числа ε выполняется соотношение 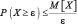или в другой форме:

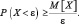
Доказательство:

Пусть X – непрерывная случайная величина с плотностью распределения f(x). Тогда её математическое ожидание

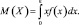
Разобьем отрезок интегрирования [0, ∞) на [0, ε) и [ε, ∞).

Получим

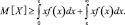
Так как оба интеграла справа положительные, то

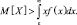
Так как x > ε, то

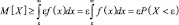
и так как M[X] > 0 (все xi (i = 1, 2, ..., n) неотрицательны), получим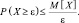

Переходя к противоположному событию

P(X < ε) = 1 – P(X ≥ ε),

получим,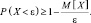

Примеры:

Пример 1. В диспетчерскую ПВРЗ поступают заявки на вызов электриков. В течение часа в среднем поступает 19 вызовов. Какова вероятность того, что в течение часа поступит вызовов:

1. Не менее 40.

2. Менее 22

Решение. Пусть случайная величина X – количество поступающих вызовов X ≥ 0. Её математическое ожидание M[X] = 19. Поэтому в соответствии с неравенством Маркова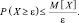

1. Найдем при ε = 40 оценку

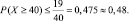
То есть вероятность того, что в течение часа поступит не менее 40 вызовов, не больше 0,48.

2. Так как требуется найти поступление менее вызовов, то

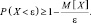
Так как ε = 22, M[X] = 19, то

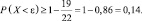
То есть вероятность того, что в течение часа поступит менее 22-х вызовов, не менее 0,14.

Пример 2. Игральная кость подбрасывается один раз. Число выпавших очков есть случайная величина X. Определить вероятность того, что она примет значение меньше 5 и оценить эту вероятность, используя закон больших чисел.

Решение.

Случайная величина X – число выпавших на кости очков, может принимать значения X1 = 1; X2 = 2; X3 = 3; X4 = 4; X5 = 5; X6 = 6.

Пусть событие Ai – выпадение цифры Xi.

Тогда число случаев k, благоприятствующих появлению события Ai, равно единице. Следовательно вероятность события Ai, 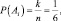события Ai(1, ..., 6) равновозможны и независимы. Составим закон распределения случайной величины X.

Тогда вероятность выпадения числа очков меньше 5 означает вероятность выпадения или одного, или двух или трех или четырех очков, то есть

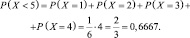
Для сравнения оценим эту величину с помощью неравенства Маркова

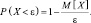
Чтобы найти математическое ожидание M[X], воспользуемся рядом распределения

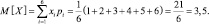
Тогда

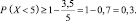
То есть вероятность того, что число выпавших очков примет значение меньше 5, не менее 0,3.

Итак, оценка вероятности, полученная с помощью неравенства Маркова, не противоречит точному значению (0,667 > 0,3).