Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Предельные теоремы теории вероятностей: учебное пособие

Селиверстова И. Ф.,

1.3. Первая теорема Чебышева (обобщенная)

Устанавливает связь между средним арифметическим наблюдаемых значений случайных величин, распределенных в общем случае по разным законам, и её математическим ожиданием.

Теорема: Если X1, X2, ..., Xn, ... независимые случайные величины с различными математическими ожиданиями 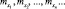и дисперсиями ограниченными сверху одним и тем же числом C 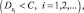то как бы ни было мало положительное число ε, вероятность неравенства 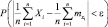будет как угодно близка к единице, если число случайных величин велико. То есть

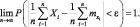
Доказательство.

Пусть X1 – значение X в первом опыте.

X1 – значение X во втором опыте и т. д.

Совокупность X1, X2, ..., Xn – n независимых случайных величин, каждая из которых распределена по своему закону.

Рассмотрим новую случайную величину.

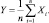
Найдем её математическое ожидание M[]. Для этого воспользуемся свойствами математического ожидания: Постоянный множитель можно вынести за знак математического ожидания; математическое ожидание суммы равно сумме математических ожиданий:

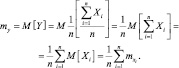
Найдем дисперсию случайной величины Y, пользуясь свойствами дисперсии: постоянный множитель выносится за знак дисперсии, возведенный в квадрат; дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин

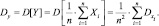
Воспользуемся неравенством Чебышева для случайных величин Y.

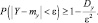
Или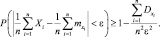

Заменим слева 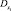большей величиной С, тогда 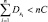и неравенство Чебышева примет вид:

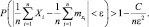
Знака равенства не стало, так как усилилось неравенство. Как бы ни было мало ε, можно выбрать n настолько большим, чтобы выполнялось неравенство: 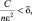где δ – сколь угодно малая положительная величина.

Тогда

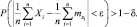
Затем, переходя к пределу при n → ∞, имеем:

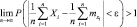(так как ).

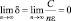Учитывая, что вероятность не может быть больше единицы, окончательно получаем

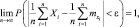
что и требовалось доказать.

В этом случае говорят, что среднее арифметическое случайных величин сходится по вероятности к его среднему математическому ожиданию.

Другими словами, при достаточно большом числе случайных величин, имеющих ограниченные дисперсии, почти достоверно, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет, по абсолютной величине, сколь угодно малым.

Здесь рассматривался случай, когда независимые случайные величины Xi (i = 1, 2) имели различные законы распределения, различные математические ожидания.

На практике часто встречаются случаи, когда случайные величины Xi распределены по одному закону и имеют одно и то же математическое ожидание. Если допустить, что их дисперсии ограниченны, то к ним можно применить теорему Чебышева.