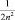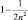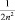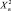Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.4. Вторая теорема Чебышева (называемая иногда законом больших чисел)
При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины X, имеющей конечную дисперсию, сходится по вероятности к её математическому ожиданию, то есть
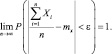
Доказательство. Пусть X1, X2, ..., Xn, ... – независимые одинаково распределенные случайные величины, а значит, они имеют одно и тоже математическое ожидание mx и одну и ту же дисперсию Dx (равномерно ограниченную).
Пусть
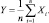
Найдем числовые характеристики случайной величины Y. Опираясь на свойства числовых характеристик, для математического ожидания M[Y] и дисперсии D[Y], получим:
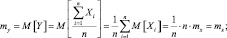
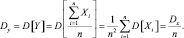
Отсюда следует, что математическое ожидание величины Y не зависит от числа опытов и равно математическому ожиданию случайной величины X.
Дисперсия величины Y неограниченно убывает с увеличением числа опытов и при достаточно большом n может оказаться сколь угодно малой.
Применим к случайной величине Y неравенство Чебышева
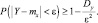
Подставим в него полученные значения my и Dy
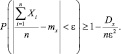
Каково бы ни было ε > 0, при увеличении n правая часть полученного неравенства стремится к единице.
Переходя к пределу и учитывая, что правая часть не может быть больше единицы, получим
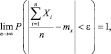
так как вероятность больше 1 быть не может. Что и требовалось доказать.
Суть и практическое значение теоремы Чебышева
Отдельные случайные величины могут иметь значения, далекие от своих математических ожиданий, а их среднее арифметическое, при большом числе случайных величин мало рассеяно и с подавляющей вероятностью принимает значения, очень близкие к среднему значению их математического ожидания.
Нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предсказать, какое значение примет их среднее арифметическое. Происходит это потому, что отклонения каждой из величин от своих математических ожиданий могут быть как положительным, так и отрицательным, а в среднем арифметическом они взаимно погашаются.
Итак, среднее арифметическое достаточно большого числа равномерно распределенных независимых случайных величин (с равномерно ограниченными дисперсиями) утрачивает характер случайной величины.
Для практического применения частного случая теоремы Чебышева, необходимо, чтобы для случайных величин X1, X2, ..., Xn, ... выполнялись условия:
1. Они должны быть попарно-независимы. Это условие выполняется, если результат каждого измерения не зависит от результатов остальных измерений.
2. Они должны иметь одно и то же математическое ожидание. Это выполняется, если нет систематических ошибок при измерении. В этом случае все математические ожидания равны истинному значению mx.
3. Их дисперсии должны быть равномерно ограниченны. (Не превышать числа С).
В этом случае вероятность 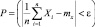 как угодно близка к единице, то есть при достаточно большом числе измерений почти достоверно, что их среднее арифметическое как угодно мало отличается от истинного значения измеряемой величины.
как угодно близка к единице, то есть при достаточно большом числе измерений почти достоверно, что их среднее арифметическое как угодно мало отличается от истинного значения измеряемой величины.
Но увеличивая число измерений, нельзя достичь сколь угодно большой их точности. Точность измерений не будет превышать точность самого прибора.
Важное практическое значение теоремы Чебышева состоит в том, что по сравнительно небольшой случайной пробе (выборке), можно судить о качестве всей генеральной совокупности однородного материала. Например, при поступлении на завод большой партии однотипных электроламп о сроке службы каждой из них судят по небольшим партиям, количество ламп в которых достаточно велико, что позволяет, согласно закону больших чисел, судить о средней продолжительности горения одной лампы. То есть, закон больших чисел имеет статистическое толкование для последовательности независимых одинаково распределенных случайных величин.
Примеры:
Пример 1. Пусть случайная величина X имеет среднее значение mx = 200 м, а среднее квадратическое отклонение σ = 5 м (Dx = 25 м2). Проведено 10000 измерений случайной величины X. Найти вероятность того, что модуль отклонения среднего арифметического значения измеренных величин 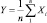 от среднего значения (mx) будет больше чем ε = 0,5, то есть найдем
от среднего значения (mx) будет больше чем ε = 0,5, то есть найдем
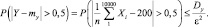
Решение. n = 10000; my = mx = 200; ε = 0,5; Dx = 25.
Пусть
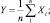
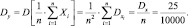
Тогда
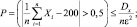
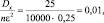
то есть
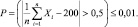
Если пренебречь вероятностью таких маловероятных событий, то можно сказать, что при 10000 измерений их среднее арифметическое наверняка будет отклонятся в ту или другую сторону не более, чем на 50 см. Чтобы достигнуть еще большей близости 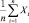 к mx, например, 10 см, то надо положить ε = 0,1 и тогда
к mx, например, 10 см, то надо положить ε = 0,1 и тогда
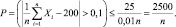
Чтобы получить вероятность менее 0,01, надо взять n = 250000. Как бы мало ни было ε правую часть можно сделать очень малой. Для этого надо взять n достаточно большим.
Пример 2. Последовательность независимых случайных величин X1, X2, ..., Xn, ... задана законом распределения
|
Xn |
–nα |
0 |
Nα |
|
pi |
|
|
|
Применима ли к заданной последовательности теорема Чебышева?
Решение. Чтобы к последовательности случайных величин можно было применить теорему Чебышева надо, чтобы выполнялись условия: взаимная независимость случайных величин, конечность их математического ожидания, они должны иметь равномерно ограниченные дисперсии. Проверим их выполняемость.
– Так как случайные величины независимы, то они и подавно попарно независимы.
– Найдем математическое ожидание:
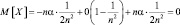
каждая случайная величина имеет конечное (равное 0) математическое ожидание.
– Найдем дисперсию n случайных величин D[X] = M[X2] – M2[X].
Составим закон распределения 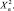
|
|
n2α2 |
0 |
n2α2 |
|
pi |
|
|
|
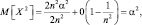
тогда
D[X] = M[X2] – M2[X] = α2 – 0 = α2,
то есть дисперсии заданных случайных величин равномерно ограниченны числом α2.
Все три условия выполняются, следовательно, к заданной последовательности применима теорема Чебышева.
Пример 3. Среднее квадратическое отклонение каждой из 2500 независимых случайных величин не превосходит 3. Оценить вероятность того, что абсолютная величина отклонения средней арифметической этих случайных величин от средней арифметической их математических ожиданий не превзойдет 0,3.
Решение: Воспользуемся теоремой Чебышева
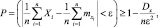
где Gx = 3; (Dx = 9) n = 2500; ε = 0,3, тогда
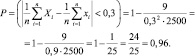
Пример 4. Пассажиры, летящие самолетом, сдают багаж в багажное отделение самолета. Оценить количество пассажиров, сдавших багаж, если с вероятностью 0,95 модуль отклонения среднего веса багажа от его нормы отличается не более, чем на 2 кг. Среднее квадратическое отклонение веса среднего багажа составляет 6 кг.
Решение: P = 0,95; ε = 2 кг; Gx = 6; Dx = 36 кг2.
Пусть случайная величина Xi вес багажа, сданного одним пассажиром.
Воспользуемся неравенством Чебышева:
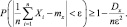
Так как
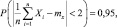
то 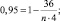
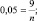
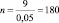 пассажиров.
пассажиров.