
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.5. Теорема Бернулли. Практическое занятие по теме «Предельные теоремы в схеме Бернулли»
Хронологически, она стоит первой среди теорем закона больших чисел и положила начало математической науке. Доказана Я. Бернулли, швейцарским математиком, весьма сложным способом. Простое доказательство дано П.Л. Чебышевым как следствие из его же теоремы.
Суть теоремы: она устанавливает связь между относительно частотой (W) появления события А в независимых испытаниях и вероятностью (p) наступления этого события в каждом опыте.
Пусть производится n независимых опытов, в каждом из которых может появится или нет некоторое событие А, вероятность появления которого в каждом опыте равна p.
Тогда теорема Бернулли утверждает: при неограниченном возрастании числа n независимых опытов, в каждом из которых событие А появляется с вероятностью p, частота (W) события А, сходится по вероятности к его вероятности p, то есть
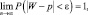
где ε – сколь угодно малое число.
Доказательство.
Пусть X1 – число появлений события А в 1-м опыте, X1 – во 2-м, …, Xn – в n-м. В каждом опыте событие А может появится или не появится. То есть каждая величина Xi (i = 1, 2, ..., n) есть дискретная случайная величина с двумя возможными значениями 0 и 1. Её ряд распределения имеет вид
|
Xi |
0 |
1 |
|
pi |
q |
P |
Где q = 1 – p.
Проверим условия выполняемости теоремы Чебышева для этой случайной величины.
1. Случайные величины X1, X2, ..., Xn взаимно-независимы, так как испытания независимы.
2. Все они имеют одинаковое математическое ожидание
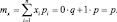
3. Дисперсии их ограниченны.
Действительно
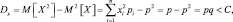 (С – const).
(С – const).
Найдем С. Для этого найдем наибольшие значения которые принимают p и q:
Пусть
y = pq = p(1 – p) = p – p2,
тогда y′ = 1 – 2p = 0 то есть 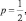 следовательно и
следовательно и 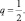
Чтобы убедиться, что это максимальное значение найдем вторую производную y″ = –2 < 0, следовательно, 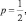
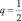 – максимальные значения, тогда можно считать
– максимальные значения, тогда можно считать 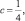 то есть
то есть 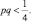
Таким образом, можно воспользоваться теоремой Чебышева
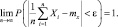
В нашем случае mx = p.
Покажем, что 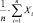 равна относительной частоте появления события А в испытаниях.
равна относительной частоте появления события А в испытаниях.
Действительно, каждая из величин Xi (i = 1, 2, ..., n) при появлении события А в соответствующем испытании принимает значение, равное единице, а в тех испытаниях, в которых событие А не появляется, принимает значение равное нулю. Поэтому их сумма
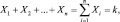
где k – число появлений события в n испытаниях
Значит 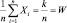 – относительная частота появления события А.
– относительная частота появления события А.
Тогда
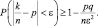
Окончательно получаем
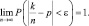
Следовательно 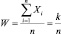 сходится по вероятности к общему математическому ожиданию этих случайных величин, то есть вероятность неравенства
сходится по вероятности к общему математическому ожиданию этих случайных величин, то есть вероятность неравенства 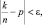 стремится к 1.
стремится к 1.
Заметим что с ростом числа испытаний 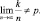 Речь идет о вероятности того, что при достаточно большом числе испытаний относительная частота
Речь идет о вероятности того, что при достаточно большом числе испытаний относительная частота  появления события А будет как угодно мало отличаться от постоянной вероятности p наступления события А в каждом опыте.
появления события А будет как угодно мало отличаться от постоянной вероятности p наступления события А в каждом опыте.
Поясним различие: 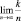 означает, что начиная с некоторого n = N выполняется неравенство
означает, что начиная с некоторого n = N выполняется неравенство 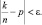 Стремление
Стремление  к p по вероятности, при n → ∞ означает, что для отдельных значений n неравенство может не выполнятся. Итак, теорему Бернулли можно записать
к p по вероятности, при n → ∞ означает, что для отдельных значений n неравенство может не выполнятся. Итак, теорему Бернулли можно записать 
Теорема Бернулли утверждает устойчивость частоты при постоянных условиях опыта, когда частота p появления события А в каждом опыте одинакова.
Замечание.
Более общий случай, когда условия опытов не одинаковы, и вероятности p1, p2, ..., pn наступления события А в каждом опыте различны, описывается теоремой Пуасcона.
