Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.7. Задачи (закон больших чисел)
1. В цехе производят резиновые манжеты для тормозной системы магистрального локомотива в количестве 400 шт. Вероятность брака при изготовлении одной манжеты p = 0,2. Пользуясь неравенством Чебышева, оценить какова вероятность того, что число бракованных манжет будет заключено в пределах от 70 до 90 штук?
2. Вероятность отклонения случайной величины X от её математического ожидания M[X] по модулю меньше, чем 0,6. Оценить значение ε, если дисперсия Dx = 0,06.
3. На грузовой двор за время Т поступают n порожних вагонов. С вероятностью p = 0,25 каждый из них требует очистки. С помощью неравенства Чебышева оценить число вагонов поступающих на грузовой двор, если вероятность того, что число вагонов, требующих очистки отличается от их математического ожидания по модулю, не более, чем на ε = 10, равна 0,008.
4. Стрелок делает 3 выстрела по мишени. Вероятность того, что он поразит мишень с одного раза, равна 0,7. Составить ряд распределения числа попаданий стрелком в мишень и оценить с помощью неравенства Чебышева, вероятность того, что отклонение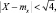 
где mx – математическое ожидание числа поражений мишени.
5. В цехе на трех станках производят заготовки для болтов. Средняя производительность одного станка 350 штук за смену. Оценить, с помощью неравенства Маркова вероятность того, что наудачу выбранный станок производит не более 500 заготовок для болтов.
6. Среднее количество грузовых поездов, проходящих за сутки через станцию А, равно 20. Оценить вероятность того, что в течение суток через эту станцию пройдет не менее 30 поездов.
7. Стрелок стреляет по мишени 4 раза. Вероятность поражения мишени при одном выстреле p = 0,7. С помощью неравенства Маркова оценить вероятность того, что мишень будет поражена:
а) не менее 3-х раз;
б) менее 4-х раз.
8. Последовательность независимых случайных величин Xi (i = 1, 2, 3, ..., n), задана законом распределения
|
Xi |
–1 |
0 |
1 |
|
pi |
|
|
|
Определить, применима ли к этой последовательности теорема Чебышева.
9. Случайная величина Xi (i = 1, 2, 3, ..., n), распределена по закону N(m; σ2) = N(0; 5). Для повышения точности замера, проведено 20 измерений. Какова вероятность того, что ошибка измерений не превзойдет 1 мк.? Определить эту ошибку, если закон распределения неизвестен, а D[X] = 4 мк2 (применить неравенство Чебышева)
10. В цехе штампуют клеммные болты для крепления рельсов. Длина каждого болта имеет среднее квадратическое отклонение 3 мм. За время Т цех изготавливает 2500 болтов. Найти вероятность того, что абсолютная величина отклонения среднего арифметического этих случайных отклонений от среднего арифметического их математических ожиданий по модулю, не превысит 0,3.
11. Сколько надо приобрести заготовок для изготовления коленчатых валов, чтобы, с вероятностью не менее 0,96, гарантировать отклонение средней арифметической брака заготовок, от математического ожидания их брака, по модулю, не более чем на 2 шт., если ранее установлено, что среднее квадратическое отклонение появления бракованной заготовки равно 3.
12. Сколько надо отобрать изделий, чтобы с вероятностью не меньшей 0,85 доля стандартных изделий отличалась от вероятности p = 0,9 каждого изделия удовлетворять стандарту по абсолютной величине не более, чем на 0,03.
13. Для монтажа схемы электрической передачи на постоянном токе электровоза было приобретено 1000 резисторов одного номинала. Вероятность брака для каждого резистора равна 0,04. Какова вероятность того, что в партии из 100 резисторов выявиться отклонение от установленной вероятности брака по абсолютной величине меньше, чем на 0,01.
14. На участке железнодорожного пути АВ в течение месяца проходит 1000 составов. Вероятность одному составу потерпеть аварию равна 0,01. Какова вероятность того, что отклонение относительной частоты аварии от вероятности аварии для одного состава по абсолютной величине не превысит 0,2?
15. На склад предприятия поступила большая партия изделий. Для проверки их качества проводятся независимые испытания. Сколько надо их провести, то есть, какую выборку изделий из партии надо взять, чтобы вероятность отклонения по модулю частоты появлений брака в выборке от вероятности каждого изделия оказаться бракованным, составляющей не более 0,07, превысила 0,76. Вероятность появления брака в отдельном испытании изделия p = 0,7.
16. На железнодорожном вокзале кассир обслуживает в течение месяца 10000 пассажиров. Вероятность допустить ошибку при оформлении билета (событие А) равна 0,3. Оценить вероятность того, что при оформлении 10000 билетов отклонение частоты события А от вероятности ошибки при оформлении одного билета по абсолютной величине не превысит 0,01.
Ответы к задачам:
1. 
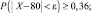
2. ε = 0,15;
3. n = 529;
4. 
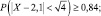
5. P(X ≥ 500) ≤ 0,33;
6. P(X ≥ 30) ≤ 0,67;
7. а) P(X ≥ 3) ≤ 1;
б) P(X < 4) ≥ 0,3;
8. Да;
9. a)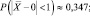 
б)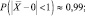 
10. 
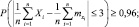
11. n = 57;
12. n = 667;
13. 
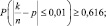
14. 
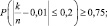
15. n = 179;
16. 