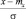Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Предельные теоремы теории вероятностей: учебное пособие

Селиверстова И. Ф.,

2. Центральная предельная теорема. Практическое занятие по теме «Центральная предельная теорема»

Второй группой предельных теорем является центральная предельная теорема. Все её формы относятся к установлению условий, при которых возникает самый распространенный в случайных явлениях нормальный закон распределения, который при увеличении числа опытов n является предельным для других законов.

Нормальное распределение возникает, когда суммируются большое число независимых случайных величин, сравнимых по порядку своего влияния на рассеивание суммы.

Практически центральной предельной теоремой можно пользоваться, когда имеется сумма небольшого числа случайных величин. При суммировании независимых случайных величин, сравнимых по своему рассеиванию, с увеличением числа слагаемых закон распределения суммы очень скоро становится приблизительно нормальным. Из практики следует, что в приближенных оценках при числе слагаемых порядка десяти (часто меньше) закон распределения суммы может быть заменен нормальным.

Примером применения центральной предельной теоремы служит нахождение ошибки в измерениях. Она является суммой малых ошибок, возникающих из-за действия случайных факторов (температура, влажность, состояние прибора, состояние наблюдателя и т. д.)

Другим примером может служить рассеивание снарядов при стрельбе. На траекторию движения снаряда воздействует много независимых факторов, влияние каждого из которых невелико. Это влияние атмосферного давления, изношенности орудия, точность наводки и т. д.

В обоих случаях имеет место приблизительно нормальный закон распределения случайной величины.

В общей форме задача была поставлена и исследована П.Л. Чебышевым, но условия были довольно ограниченными. При весьма общих условиях она была доказана в 1900 году учеником П.А. Чебышева академиком А.М. Ляпуновым. Для некоторых частных условий её доказали еще в 18 веке А. Муавр и П. Лаплас. Теорема Ляпунова занимает важнейшее место.

Теорема Ляпунова (без доказательства):

Пусть X1, X2, ..., Xn, ... последовательность независимых случайных величин с математическим ожиданием M[Xi] = mx. Если дисперсии этих случайных величин 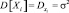конечны и отличны от нуля, то при достаточно больших n закон распределения суммы X1 + X2 + ... + Xn будет сколь угодно близок к нормальному закону распределения.

По условию теоремы случайные величины независимы, поэтому

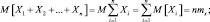
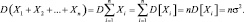
То есть, при больших n закон распределения суммы 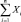близок к нормальному N(nmx, nσ2). Параметры его nmx и nσ2 возрастают с увеличением n. Поэтому удобно рассматривать нормированные суммы 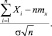Такие суммы при n → ∞ имеют закон распределения N(0, 1).

То есть

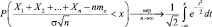
(по определению F(x) = P(X < x)). Для нормального распределения

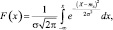
а для нормированного

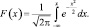
Замечание:

Существуют варианты для слагаемых с разными распределениями, для слабо зависимых величин и так далее. Но во всех вариантах суть одна:

Если случайная величина может быть представлена в виде суммы большого числа независимых (или слабо зависимых) случайных величин, каждая из которых мала по сравнению с суммой, то эта величина имеет закон распределения близкий к нормальному.

На практике центральная предельная теорема решает вопросы о вероятности наступления события А в процессе испытаний k – раз или о вероятности его наступления в интервале (k1, k1).

Прежде, чем получить их математическое содержание вспомним свойства нормального закона распределения случайных величин.

Он описывается функцией распределения F(x) случайной величины X. Функция распределения F(x) действительной переменной x определяется вероятностью того, что случайная величина X примет значение меньшее x, то есть

F(x) = P(X < x).

Заметим, что функция F(x) отражает общий способ задания случайной величины (дискретной и непрерывной)

Общие свойства, функции распределения F(x)

1. Значения F(x) принадлежат отрезку [0, 1], 0 ≤ F(x) ≤ 1, так как (0 ≤ P(A) ≤ 1), то есть, если все значения случайной величины принадлежат отрезку (a, b), то F(x) = 0 при X ≤ a (невозможное событие) и F(x) = 1, при X ≥ b (достоверное событие).

Расширяя пределы (a, b) до (–∞, +∞), получим F(–∞) = 0; F(+∞) = 1.

2. F(x) – функция неубывающая, то есть F(x2) > F(x1), если x2 > x1. На языке вероятностей это означает

P(X < x2) = P(X < x1) + P(x1 ≤ X < x2).

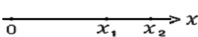
То есть случайная величина X попадает в промежуток, расположенный левее x1 или в промежуток [x1, x2), так как события несовместны. Тогда

P(x1 ≤ X < x2) = P(X < x2) – P(X < x1).

Значит

P(x1 ≤ X < x2) = F(x2) – F(x1).

Для интервала (a, b), формула примет вид

P(a ≤ X < b) = F(b) – F(a) при a < b.

Так как

P(a ≤ X < b) > 0,

то F(b) – F(a) > 0 или F(b) > F(a), что означает, что F(x) – неубывающая.

Так как вероятность для непрерывной случайной величины принять определенное значение равна 0, то

P(a ≤ X < b) = P(a < X < b) = = P(a < X ≤ b) = P(a ≤ X ≤ b).

Например:

P(a < X ≤ b) = P(a < X < b) + P(X = b),

но P(X = b) = 0.

Следовательно,

P(a < X ≤ b) = P(a < X < b)

и если X ∈ (a, b), то при X ≤ a; F(x) = 0, а при X ≥ b, F(x) = 1.

Рассмотрим полученное ранее соотношение

P(a ≤ X < b) = F(b) – F(a).

По формуле Ньютона – Лейбница

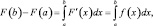
где f(x) = F′(x).

Так как

P(a ≤ X < b) = P(a < X < b)

то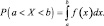

Если интервал симметричный (–a, a), то

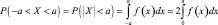
(в силу четности f(x)).

Зная f(x) можно найти F(x):

F(x) = P(X < x) = P(–∞ < X < x),

тогда (полагая a = –∞, b = x и учитывая, что

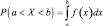
получим

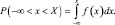
Итак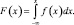

Нормальный закон распределения характеризуется плотностью вида

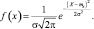
Тогда функции общего нормального распределения имеет вид

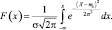
Переходя к центрированной случайной величине 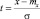при замене пределов интегрирования

для нормированного распределения случайной величины получим

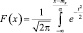– причем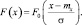

Найдем вероятность попадания нормально распределенной случайной величины X с параметрами N(mx, σ) в интервал (a, b)

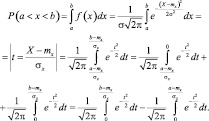
Функция 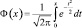называется функцией Лапласа (для нее составлены таблицы, так как интеграл 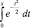в элементарных функциях не берется). С помощью этой формулы можно найти

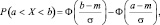
тогда