
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.1. Локальная и интегральная теоремы Муавра-Лапласа
Переходя к случайным величинам определяющим k-число появлений события А в n независимых испытаниях, в каждом из которых вероятность появления события А равно p, получим формулы для Pn(k) и Pn(k1 ≤ k ≤ k2). Для этого надо, исходя из характера распределения каждой случайной величины, найти математическое ожидание и дисперсию для суммы k появлений события А.
M[k] = nmk = np;
D[k] = nDk = npq;
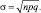
Тогда случайная величина k распределена также, как нормально распределенная случайная величина X с N(np, npq) для которой
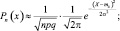
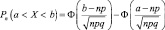 ;
;
и 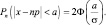
И можно записать
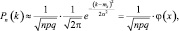
где 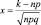 (для φ(x) составлены таблицы. Приложение 2)
(для φ(x) составлены таблицы. Приложение 2)
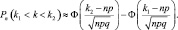
Формулы для Pn(k1) и Pn(k2 < k < k1), составляют содержание, соответственно, локальной и интегральной теорем Муавра-Лапласа.
Для вероятности отклонения случайной величины k от её математического ожидания получим
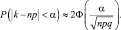
Разделим 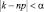 на n, и обозначим
на n, и обозначим 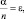 получим
получим
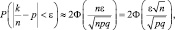
т. е. 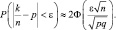
Примеры
Пример 1. Из 8 тяговых двигателей 3 не выдерживают перегрузки и выходят из строя. Какова вероятность того, что 5 из них выйдут из строя: Расчет провести, применяя:
1) локальную теорему Муавра – Лапласа;
2) по формуле Бернулли.
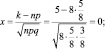
Решение: n = 8; 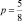 – вероятность тяговому двигателю выдержать нагрузку
– вероятность тяговому двигателю выдержать нагрузку 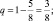 k = 5.
k = 5.
1) Воспользуемся локальной теоремой Муавра – Лапласа
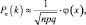
где 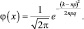 Найдем
Найдем
 φ(0) = 0,3989.
φ(0) = 0,3989.
Тогда
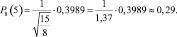
2) Воспользуемся формулой Бернулли
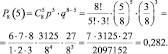
Пример 2. На участке АВ железнодорожного пути проводится контроль зазора между рельсами. Вероятность того, что зазор окажется с отклонением от нормы, в среднем равна 0,2. Какова вероятность того, что из 900 зазоров не отклонится от нормы:
а) 700 зазоров;
б) 750 зазоров.
Решение:
n = 900; p = 0,8; q = 0,2;
а) k1 = 700;
б) k1 = 750.
a) k1 = 700. По локальной теореме Муавра – Лапласа
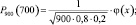
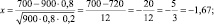
φ(–1,67) = φ(1,67) = 0,0989,
так как, по свойству функции плотности, φ(–x) = φ(x)
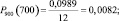
б) k2 = 750 Аналогично (а), получим:
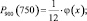
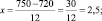
φ(x) = 0,0488,
тогда 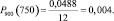
Пример 3. Ателье выпускает специальные костюмы для дорожных рабочих. Они выборочно проходят ОТК. Вероятность обнаружения брака для одного костюма равна 0,5. Сколько костюмов (k), с вероятностью 0,0456, отобранных наудачу из партии 100 костюмов, могут оказаться с браком?
Решение:
n = 100; Pn(k) = 0,0456; p = 0,2; q = 1 – p = 0,8.
Воспользуемся локальной теоремой Муавра – Лапласа
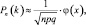
где 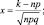
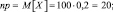
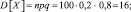
G[X] = 4.
Тогда 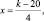 а
а 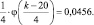
То есть,
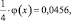
отсюда φ(x) = 4∙0,0456 = 0,1826.
По таблицам приложения 2 для φ(x) = 0,1826 находим значение x = 1,25.
Тогда
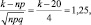
следовательно, k – 20 = 5, то есть k1 = 20 + 5 = 25, но φ(x) = φ(–x), тогда следовательно k – 20 = –5, k1 = 15.
Итак, с вероятностью 0,0456, могут оказаться бракованными от 15 до 25 костюмов.
Пример 4. Стрелок поражает мишень с вероятностью 0,7. Найти вероятность того, что при 40 выстрелах он поразит мишень:
а) не менее 30 раз;
б) от 20 до 30 раз.
Решение: Выстрелы по мишени – события независимые. Пусть Xi (i = 1, ..., 40) – поражение мишени при i-м выстреле. Тогда 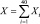 – число всех поражений мишени при 40 выстрелах. Математическое ожидание поражения при одном выстреле
– число всех поражений мишени при 40 выстрелах. Математическое ожидание поражения при одном выстреле 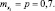 Для суммы попаданий в мишень M[X] = np = 40∙0,7 = 28. Аналогично для дисперсии
Для суммы попаданий в мишень M[X] = np = 40∙0,7 = 28. Аналогично для дисперсии
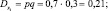
D[X] = nDx = npq = 40∙0,21 = 8,4 – для суммы поражений
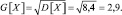
Математическое ожидание и дисперсия конечны. Следовательно, условия для применения формулы Муавра – Лапласа, выполнены.
Воспользуемся формулой:
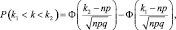
где k – число выстрелов по мишени.
а) k1 = 30; k2 = 40. Тогда:
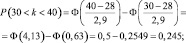
б) k1 = 20; k2 = 30. Тогда:
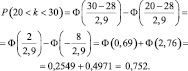
Пример 5. В университет поступили 1000 абитуриентов. Вероятность не сдать первую сессию для каждого из них равна 0,2. Найти вероятность того, что отклонение относительной частоты не сдавших студентов от вероятности каждого студента не сдать сессию по модулю не больше, чем 0,01.
Решение: Пусть X – число студентов, не сдавших сессию p = 0,2; n = 1000; ε = 0,01.
Воспользуемся формулой:
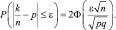
Получим:
Пример 6. Среди 1000 рабочих, занятых на строительных работах 514 имеют среднее образование. Пусть случайная величина X – число рабочих, имеющих среднее образование. Определить интервал возможного числа этих рабочих (случайной величины X), симметричный относительно математического ожидания этой величины, в который она попадает с вероятностью 0,997.
Решение: Пусть 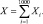 Наудачу выбранный рабочий может иметь, а может и не иметь среднего образования. Пусть Xi – рабочий имеет среднее образование с вероятностью
Наудачу выбранный рабочий может иметь, а может и не иметь среднего образования. Пусть Xi – рабочий имеет среднее образование с вероятностью 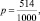 тогда
тогда
q = 1 – p = 1 – 0,514 = 0,486.
Математическое ожидание случайной величины Xi: 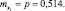
Дисперсия
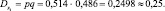
Для случайной величины X, имеем
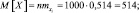
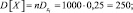
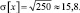
Применим центральную предельную теорему для случайной величины X, имеющей нормальное распределение, то есть:
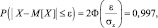
тогда 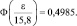 По таблицам приложения 3 для Φ(x) = 0,4985, найдем
По таблицам приложения 3 для Φ(x) = 0,4985, найдем 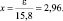 Тогда
Тогда
ε = 2,96∙15,8 = 46,77 ≈ 47.
Искомый интервал будет:
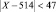 или 514 – 47 < X < 514 + 47,
или 514 – 47 < X < 514 + 47,
то есть 467 < X < 561 или (467; 561).
С большой вероятностью (P = 0,997), можно утверждать, что число рабочих со средним образованием будет находится в пределах от 467 до 561 человека.
Пример 7. Вдоль железной дороге на участке АВ высаживают лесозащитные полосы. Для этого было использовано 500 саженцев различных деревьев. Вероятность прижиться в новом грунте каждому саженцу равна 0,9. На какую величину отклонится частота прижившихся деревьев от вероятности прижиться одному дереву по модулю, если вероятность этого отклонения P = 0,997.
Решение:
n = 500; p = 0,9; q = 1 – 0,9 = 0,1; P = 0,995.
Найти ε.
Пусть 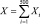 – количество прижившихся деревьев. Воспользуемся интегральной формулой Муавра – Лапласа:
– количество прижившихся деревьев. Воспользуемся интегральной формулой Муавра – Лапласа:
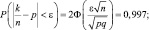
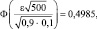
следовательно, 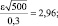 тогда
тогда 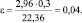
Пример 8. Контроль исправности прибора занимает время от 4 до 10 минут. Контролеру предстоит проверить 46 приборов. Временной интервал контроля [4, 10] для каждого прибора равновероятен. Найти вероятность того, что контролер справится с работой за 6 часов (360 мин).
Решение: Пусть Xi – время проверки i-го прибора. Тогда X = X1 + X2 + ... + X500. То есть минимальное время проверки прибора составит 46∙4 = 184 мин. Надо найти P(X ≤ 360), то есть P(184 ≤ X ≤ 360). Так как все Xi равновозможны на [4, 10], то случайная величина Xi имеет равномерный закон распределения. Тогда числовые характеристики Xi
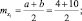
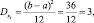
следовательно, для 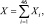 где Xi – независимая случайная величина, получаем
где Xi – независимая случайная величина, получаем
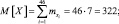

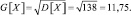
Так как Xi – независимые случайные величины, имеющие конечные математические ожидания 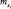 и дисперсию
и дисперсию 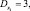 то по центральной предельной теореме случайная величина X имеет закон распределения близкий к нормальному N(M[X]; σ2) = N(322; 138).
то по центральной предельной теореме случайная величина X имеет закон распределения близкий к нормальному N(M[X]; σ2) = N(322; 138).
Тогда для нахождения P(X ≤ 360) воспользуемся формулой:
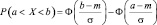
и таблицей функций Лапласа (Приложение 3). Получим
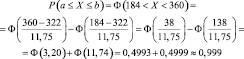
(где а =184 – минимальное время проверки прибора).
Пример 9. На товарный двор в течение 30 минут под погрузку прибывает в среднем 15 машин. Погрузка производится круглосуточно. Поток машин пуассоновский. Определить доверительные границы количества прошедших погрузку машин при заданной надежности 0,95.
Решение. Пусть Xi – среднее число машин, прошедших погрузку в течение каждого из 24 часов, а 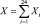 – общее число машин прошедших погрузку за сутки. Тогда
– общее число машин прошедших погрузку за сутки. Тогда  а
а
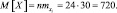
Так как поток пуассоновский (простейший), т. е. обладающий свойствами стационарности, отсутствия последействия, ординарности, то
М[X] = D[X] = 720.
Воспользуемся приближенной формулой:
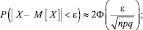
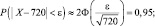
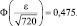
По приложению 3 находим 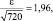 откуда
откуда
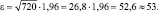
Тогда 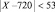 или
или 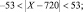 720 – 53 < X < 720 + 53 или 667 < X < 773.
720 – 53 < X < 720 + 53 или 667 < X < 773.
Итак, количество машин, прошедших погрузку, при заданной надежности 0,95 находится в интервале (667; 773).
