
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2. Задачи (Центральная предельная теорема)
1. В составе поезда дальнего следования едут 700 пассажиров. В билет включен страховой взнос 100 у.е.
П
Вероятность наступления несчастного случая для каждого пассажира равна 0,03. При этом пассажиру выплачивается 1000 у.е. Найти вероятность того, что при выполнении рейса железная дорога потерпит убытки.
2. 85 % локомотивов безотказно работают в течение гарантийного срока. Найти вероятность того, что среди контролируемых 100 локомотивов не менее 80 проработают безотказно в течение гарантийного срока.
3. На вагоноремонтном заводе на каждую 1000 работающих приходиться 800 мужчин. Найти вероятность того, что доля мужчин из 200 наудачу отобранных рабочих будет отличаться от вероятности того, что работник оказался мужчиной по абсолютной величине не более чем на 0,05.
4. Завод выпускает тележки для колесных пар. Из них 5 % бракованные. Наудачу выбирают 50 тележек. Найти вероятность того, что число небракованных тележек окажется в пределах от 45 до 48.
5. Найти вероятность того, что в результате 1000 бросаний монеты число выпадений герба будет в интервале [475, 525].
6. Юрист консультирует клиента от 5 до 15 минут. Ему придется проконсультировать 40 человек. Считая для каждого клиента равновозможными все значения времени консультации от 5 до 15 минут, оценить вероятность того, что юристу на это потребуется не меньше 6 часов.
7. Поезда метро идут с интервалами 2 минуты. Каждый из пассажиров независимо от других приходит на платформу в случайный момент времени и ожидает ближайшего поезда. В поезд зашло 75 пассажиров. Найти приближенно вероятность того, что их суммарное время ожидания, превысило 1 час.
8. Вагонные буксы проходят стендовые испытания, причем 80 % из них соответствуют стандарту. Сколько надо отобрать букс, чтобы с вероятностью, равной 0,995 можно было надеяться, что доля стандартных букс будет отличаться от вероятности изготовления стандартной буксы в обе стороны (по модулю) не более, чем на 0,06?
9. При поверке качества транзисторов установлено, что 80 % из них служат не меньше гарантийного срока. Наудачу выбирают 500 транзисторов. Найти вероятность того, что отклонение по абсолютной величине доли транзисторов с гарантийным сроком службы от вероятности одному транзистору выдержать испытания на гарантийный срок, будет не больше 0,04?
10. Складываются случайные величины Xi, где i (1, ..., 21). Они равномерно распределены в интервале [0, 2]. Написать приближенное выражение плотности распределения суммы этих случайных величин. Найти вероятность того, что их сумма будет заключена в пределах от 15 до 17. Найти вероятность того, что случайная величина X, примет значение равное 10.
11. Поезд следует мимо светофора. Вероятность того, что при приближении каждого поезда он сработает, равна 0,99. Найти вероятность того, что при прохождении 1000 поездов, он сработает в 995 случаях.
12. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность его появления в каждом испытании равна 0,2.
13. В управление железной дороги отправили 1000 компьютеров. Вероятность повреждения одного из них при транспортировке равна 0,001. Какое число компьютеров может быть повреждено при их транспортировке с вероятностью 0,054?
14. Из 1000 колесных пар, гарантийный срок вырабатывают 990. Исследуется 4000 колесных пар на соответствие гарантийному сроку службы. На какую величину по модулю отклонится частота, выдержавших гарантийный срок колесных пар, от вероятности выдержать его для одной пары, если эта граница должна быть гарантированна с вероятностью 0,9954?
15. Пассажир опаздывает на поезд с вероятностью 0,06. Какова вероятность того, что среди 800 пассажиров число опоздавших составит от 46 до 50 человек.
Ответы к задачам:
1. P(70 ≤ k ≤ 700) ≈ 0,0082;
2. P(80 ≤ k ≤ 100) = 0,919;
3. 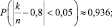
4. P(45 ≤ k ≤ 48) ≈ 0,573;
5. P(457 ≤ k ≤ 525) ≈ 0,8858;
6. P(X ≤ 360) = P(200 ≤ X ≤ 360) = 0,9856;
7. P(X > 60) = P(60 < X ≤ 150) = 0,9986;
8. n = 351;
9. 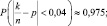
10. a) 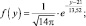
б) P(15 ≤ Y ≤ 17) ≈ 0,0614;
в) P(k = 10) ≈ 0,049;
11. P1000(995) ≈ 0,035;
12. P400(80) ≈ 0,0498;
13. k = 3;
14. ε ≈ 0,033;
15. P800(46 < X < 50) ≈ 0,23.
