Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ГИБРИДНОЕ МОДЕЛИРОВАНИЕ МУЛЬТИАГЕНТНЫХ ПРОЦЕССОВ ПРЕОБРАЗОВАНИЯ РЕСУРСОВ

Аксенов К. А., Гончарова Н. В.,

3.3.2. Реализация механизма логического вывода на основе языка Transact-SQL

Как отмечено в работе [6], «чтобы системы с базами знаний, основанные на фреймовых системах, извне выглядели интеллектуальными, при их проектировании необходимо предусматривать применение в составе системы присоединенных процедур. Иначе их трудно будет отличить от обычных программ обработки данных». В данном разделе решается задача обоснования реализации механизма логического вывода на основе языка Transact-SQL.

Рассмотрим решение примера «классической» задачи на основе подхода, изложенного в разделе 2.4.2. Пример описан в [119] и демонстрирует следующие аспекты фреймов: значения по умолчанию, демоны, множественное наследование.

В данном примере рассматривается предметная область оценки недвижимости – необходимо провести оценку примерной стоимости на рынке земельных участков, полная информация о которых отсутствует. Большинство участков имеет, как правило, форму выпуклых прямоугольников, поэтому можно оценить стоимость участков, предполагая, что те, о которых идет речь, также имеют подобную форму, если только нет конкретной информации об обратном. Предположим, что цепочка «КВАДРАТ à ПРЯМОУГОЛЬНИК à ПАРАЛЛЕЛОГРАММ à ТРАПЕЦИЯ à ЧЕТЫРЕХУГОЛЬНИК à МНОГОУГОЛЬНИК» представляет знания о плоских геометрических фигурах, которые можно использовать для логических рассуждений о форме участков. Каждый узел в этой цепи имеет связанную с ним структуру записей (фрейм), формат которой приведен ниже [119].

NAME (ИМЯ):

Number of sides (Количество сторон):

Length of sides (Длины сторон):

Size of Angles (Углы):

Area (Площадь):

Price (Цена):

Практически все слоты фрейма Многоугольник придется оставить незаполненными, поскольку ничего нельзя сказать о сторонах и углах типичного многоугольника. Однако для слота Количество сторон в качестве значения по умолчанию можно установить 4, поскольку подавляющее большинство земельных участков имеет форму четырехугольника. Таким образом, все земельные участки, информация о форме контура которых отсутствует, будут полагаться четырехугольными. Слот Площадь также нельзя заполнить, но известно, как вычислить площадь многоугольника, располагая другой информацией о нем. Любой n-сторонний многоугольник можно разбить на п – 2 треугольника, вычислить их площади и затем просуммировать результаты. Программу, реализующую эту процедуру, можно подключить к слоту Площадь. Процедуры, подключенные к структуре данных и запускаемые на выполнение при появлении запроса или обновлении информации в структуре, называют демонами. Те демоны, которые по запросу вычисляют некоторые значения, называются демонами по требованию (IF-NEEDED) [119].

Полезно также иметь демон, который при заполнении слота Площадь сразу вычислял бы цену участка. Эта процедура относится к другому типу демонов – демонам добавления (IF-ADDED) – и подключается также к слоту Площадь. Теперь при обновлении или установке значения слота Площадь автоматически будет вычислена цена участка, а результат будет помещен в слот Цена.

Перейдем к следующему уровню в иерархии фреймов. Для фрейма Четырехугольник совершенно очевидно нужно установить значение 4 в слот Количество сторон. Это значение будет наследоваться фреймами на каждом из последующих уровней иерархии. Вычислять площадь и цену всех фигур, представленных фреймами последующих уровней, можно тем же способом, что и для многоугольника. Поэтому описанные выше демоны также могут быть унаследованы всеми последующими фреймами. Но для четырехугольника можно примерно оценить площадь, даже не располагая информацией о значениях внутренних углов контура, а зная только длины сторон. Вполне приемлемые результаты можно получить с помощью следующего эвристического способа: среднюю длину стороны для одной пары противолежащих сторон умножить на среднюю длину стороны для другой пары. Этот метод даст существенную ошибку только для четырехугольников, не являющихся выпуклыми, а такое встречается очень редко [119].

Эта эвристика может быть реализована в виде демона по требованию, подсоединенного к слоту Площадь фрейма Четырехугольник. Такой демон должен выполнять следующее:

– если имеется информация о величинах углов четырехугольника и длинах сторон, то необходимо вызывать демон фрейма Многоугольник и выполнять точное вычисление площади;

– если имеется только информация о длинах сторон четырехугольника, то следует выполнять вычисление по приближенному эвристическому методу;

– если отсутствует любая информация о параметрах четырехугольника, никаких вычислений выполнять не нужно.

Фреймы, представляющие все последующие разновидности четырехугольников, наследуют значение из слота Количество сторон фрейма Четырехугольник. Но в каждом из этих фреймов можно реализовать свою процедуру вычисления площади, лучше учитывающую особенности именно данного вида фигур. Например, площадь трапеции можно вычислить как произведение высоты на среднюю длину оснований, а фреймы прямоугольника и квадрата могут унаследовать эту процедуру у параллелограмма, площадь которого равна произведению основания на высоту [119].

Ниже приводятся листинги скриптов создания хранимых процедур, вычисляющих площади параллелограмма, прямоугольника и треугольника.

/*---------------------------------------------------------------------------*/

/*---------------------------------------------------------------------------*/

/*

Параллелограмм – четырехугольник, у которого стороны попарно параллельны.

-------------------------------------

--вычислить площадь параллелограмма

--@a-длина одной стороны,

--@b – длина следующей стороны,

--@aa – угол между сторонами @a и @b в градусах,

--@S-результат (площадь)

*/

CREATE PROCEDURE sp_Parallelogram (@a DECIMAL(6,2), @b DECIMAL(6,2), @aa FLOAT, @S DECIMAL(6,2) OUT)

AS

SELECT @S = @a*@b*SIN(@aa*PI()/180)

GO

/*---------------------------------------------------------------------------*/

/*---------------------------------------------------------------------------*/

/*

Прямоугольник – четырехугольник, у которого все углы прямые.

------------------

вычислить площадь прямоугольника,

где@a – длина одной стороны,

@b – длина следующей стороны,

@s – результат, площадь.

*/

CREATE PROCEDURE sp_Restangle (@a DECIMAL(6,2), @b FLOAT, @S DECIMAL(6,2) OUT)

AS

SELECT @S = @a*@b

GO

/*---------------------------------------------------------------------------*/

/*---------------------------------------------------------------------------*/

/*

Треугольник – многоугольник с тремя сторонами.

--

площадь треугольника

@a, @b – 2 смежные стороны

@ab – угол между ними, в градусах

@s-результат

*/

CREATE PROCEDURE sp_Treangle (@a DECIMAL (6,2), @b DECIMAL (6,2), @ab DECIMAL(6,2), @s DECIMAL (6, 2) OUT)

AS

SELECT @S = 0.5*@a*@b *sin (@ab * pi()/180)

GO

/*---------------------------------------------------------------------------*/

/*---------------------------------------------------------------------------*/

Ниже приводится хранимая процедура вычисления стоимости площади многоугольника:

/*---------------------------------------------------------------------------*/

/*---------------------------------------------------------------------------*/

CREATE PROCEDURE sp_Area (

@TypeOfFigure VARCHAR(50), --типфигуры

@NumberOfSides SMALLINT = 4, -- количество сторон, по умолчанию четырехугольник

@LengthOfSides VARCHAR(255) = ‘’, --длины сторон, разделенные спец. символом ‘!’ в м2, указываются в последовательности друг за другом

--н-р ‘6.2!7.8!8.1!9.3!’

@SizeOfAngless VARCHAR(255) = ‘’, --углы в градусах, начиная с угла между первой и второй стороной указанной в параметре @LengthOfSides

--н-р, ‘30!40!50!’

@StrOfTreangle VARCHAR(255) = ‘’, --при расчете площади многоугольника – метод разбиения на треугольники, необходимо задать

--стороны и угол между ними, в формате ‘сторона1:сторона2:угол между ними:!’сторона1:сторона2:угол между ними:!

@PriceOfM MONEY = 0,--стоимость метра квадратного

@Price MONEY = 0 OUT) --стоимость участка

AS

DECLARE @tblOfSides TABLE (ID INT, VAL FLOAT)

DECLARE @tblOfAngless TABLE (ID INT, VAL FLOAT)

DECLARE @tblofTreangle TABLE (ID INT, VAL VARCHAR(100), state TINYINT)

DECLARE @Area FLOAT, @a FLOAT, @b FLOAT, @S DECIMAL (6,2), @aa FLOAT

DECLARE @cnt INT, @id INT

SELECT @Area = 0, @Price = 0, @S = 0

SELECT @cnt = 0

--процедура формирования из строки – табличного представления

INSERT INTO @tblOfSides ([id], val)

SELECT* FROM dbo.FromStrToTable(@LengthOfSides, ‘!’)

INSERT INTO @tblOfAngless ([id], val)

SELECT* FROM dbo.FromStrToTable(@SizeOfAngless, ‘!’)

IF (@NumberOfSides > 4) BEGIN

INSERT INTO @tblOfTreangle (id, val)

SELECT * FROM dbo.FromStrToTable (@StrOfTreangle, ‘!’)

UPDATE @tblOfTreangle SETState = 0

SELECT @cnt = COUNT(*) FROM @tblOfTreangle WHEREState = 0

WHILE @cnt > 0 BEGIN

DELETE FROM @tblOfSides

SELECT TOP 1 @id = id, @LengthOfSides = Val FROM @tblOfTreangle WHEREState = 0

INSERT INTO @tblOfSides

SELECT* FROM dbo.FromStrToTable(@LengthOfSides, ‘:’)

SELECT @a = (SELECT Val FROM @TblOfSides WHERE ID = 1)

SELECT @b = (SELECT Val FROM @TblOfSides WHERE ID = 2)

SELECT @aa = (SELECT Val FROM @TblOfSides WHERE ID = 3)

EXEC sp_Treangle @a, @b, @aa, @s OUT

SELECT @cnt = COUNT(*) FROM @tblOfTreangle WHEREState = 0

SELECT @Area = @Area + @s

UPDATE @tblOfTreangle SETState = 1 WHERE id = @id

END

END

IF (@NumberOfSides = 4) BEGIN

--если тип фигуры не определен, и углы неизвестны, но известны длины -- > то общая формула для четырехугольника:

--средняя длина стороны для одной пары противолежащих сторон умножить на среднюю длину стороны для другой пары

IF (UPPER(@TypeOfFigure) = ‘NONAME’) AND ((SELECT COUNT(*) FROM @TblOfSides) = 4) AND (SELECT COUNT(*) FROM @TblOfAngless) = 0 BEGIN

SELECT @Area = (SELECT AVG(VAL) FROM @TblOfSides WHERE ID IN (1, 3))* (SELECT AVG(VAL) FROM @TblOfSides WHERE ID IN (2, 4))

END

--квадрат

IF (UPPER(@TypeOfFigure) = ‘квадрат’) AND ((SELECT COUNT(*) FROM @TblOfSides) > = 1) BEGIN

SELECT @a = (SELECT Val FROM @TblOfSides WHERE ID = 1)

EXEC sp_Restangle @a, @a, @Area OUT

END

--прямоугольник

IF (UPPER(@TypeOfFigure) = ‘прямоугольник’) AND ((SELECT COUNT(*) FROM @TblOfSides) > = 1) BEGIN

SELECT @a = (SELECT Val FROM @TblOfSides WHERE ID = 1)

SELECT @b = (SELECT Val FROM @TblOfSides WHERE ID = 2)

EXEC sp_Restangle @a, @b, @Area OUT

END

--трапеция

IF (UPPER(@TypeOfFigure) = ‘Параллелограмм’) AND ((SELECT COUNT(*) FROM @TblOfSides) > = 2) AND ((SELECT COUNT(*) FROM @TblOfSides) > = 1) BEGIN

SELECT @a = (SELECT Val FROM @TblOfSides WHERE ID = 1)

SELECT @b = (SELECT Val FROM @TblOfSides WHERE ID = 2)

SELECT @aa = (SELECT Val FROM @TblOfAngless WHERE ID = 1)

EXEC sp_Parallelogram @a, @b, @aa, @Area OUT

END

--трапеция

IF (UPPER(@TypeOfFigure) = ‘ромб’) AND ((SELECT COUNT(*) FROM @TblOfSides) > = 1) AND ((SELECT COUNT(*) FROM @TblOfSides) > = 1) BEGIN

SELECT @a = (SELECT Val FROM @TblOfSides WHERE ID = 1)

SELECT @aa = (SELECT Val FROM @TblOfAngless WHERE ID = 1)

EXEC sp_Parallelogram @a, @a, @aa, @Area OUT

END

END

IF @Area > 0 BEGIN

SELECT @Price = @Area * @PriceOfM

END

SELECT Price = @Price

GO

/*----------------------------------------------------------------*/

/*----------------------------------------------------------------*/

На рис. 3.3–3.5 приводятся примеры вычисления стоимости участков различной формы в QueryAnalyzer (утилита MSSQLServer):

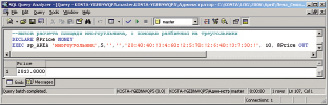
Рис. 3.3. Вызов расчета стоимости площади многоугольника, с помощью разбиения на треугольники

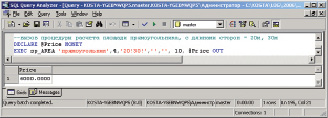
Рис. 3.4. Вызов расчета стоимости площади прямоугольника

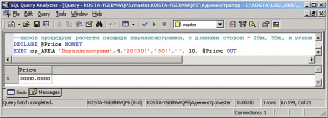
Рис. 3.5. Вызов расчета стоимости площади параллелограмма

В целом можно выделить следующие варианты применения языка Transact-SQL для реализации функции логического вывода в мультиагентной системе преобразования ресурсов:

– механизм вывода (алгоритм) ИА полностью или частично оформлен в виде хранимой процедуры и каждый раз вызывается планировщиком;

– части правил ИА содержат или запросы к БЗ на языке Transact-SQL, или ссылки на хранимые процедуры, которые реализуют функции поиска и/или расчетов (вычислений);

– решение задач поиска и вычислений на фрейм-системе (так как модели реальных МАС преобразования ресурсов имеют большую размерность).