
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

АВТОПРОЕКТИРОВАНИЕ ГОРНЫХ МАШИН В 3D: ПРОЕКТНО-МОДЕЛЬНЫЙ ПОДХОД
Бейсембаев К. М., Жолдыбаева Г. С., Дёмин В. Ф., Малыбаев Н. С., Шманов М. Н.,
1.2.2. Численное моделирование движения многозвенных механизмов
Важным элементом оптимизации кинематических схем является их моделирование на компьютерах. Исследовательские работы должны выполняться на основе программ разработанных авторами, поскольку при корректном исполнении это подразумевает фундаментальные знания движущих процессов в статике и динамике. Кроме того автор уже «видит», какие исследования надо произвести и они логически вытекают из разработки, автору понятны и ограничения пакета, пути его дальнейшего совершенствования. В этом случае использование специализированных зарубежных пакетов существенно расширит возможности авторского, правила его неформального использования (функций стандартного пакета и возможные ошибки обычно не полностью указываются разработчиками). В настоящее время эти функции выполняются пакетом ADAMS. К кинематическим расчётам обычно относят и определение геометрических параметров механизмов, действующих в них сил, причем все эти параметры определяются по траектории движения системы (можно говорить, что определяется аттрактор многозвеньевой системы).
Заметим, что студенту эти методы знакомы из курса теории механизмов и машин и в основном на основе графическо-аналитических методов, когда в многозвенном механизме, определяются независимые группы элементов, статическая определимость которых возможна. Искомые параметры определяются построением плана положений механизма на чертеже, и затем построения по нему плана действующих сил, скоростей и ускорений. Это обусловлено тем, что уже при четырех звеньях аналитическое определение геометрической схемы затруднительно из-за необходимости решения тригонометрических уравнений высокой степени, связывающих параметры механизмов [6–8].
Объектно-ориентированные языки программирования принципиально не отличаются друг от друга (VBA, Delphi, C++) и реализуют близкие алгоритмы, (рис. 1.2–1.5).
В рамках рассматриваемой задачи в различных приложениях решения мало чем отличаются.
Ниже приведён алгоритм численного решения определения геометрических параметров рычажных механизмов, реализованный на VBA. Заметим, что в самих приложениях приобретенных на западе, код решений просмотреть не удаётся, что существенно сдерживает применение пакетов.
Координаты Y шарнира А (рычаг r1) и В (рычаг r2):
Y1 = r1*sin (a1)
Y2 = r2*sin (a2)
Формулы ведены в ячейки листа
Координаты X шарнира А (рычаг r1) и В (рычаг r2):
X1 = r1*cos (a1)
X2 = r2*cos (a2)
Формулы введены в ячейки электронной таблицы (рисунок 1.2), здесь же введены исходные данные, размеры рычагов и величины L, а также величины углов наклона рычага а1, или просто а. Угол а2 в общем не равен углу а1, но определяется им и размерами четырёхзвенника. Очевидно, что связь этих параметров можно построить из уравнения, выражающего величину квадрата L
L2 = (Y2–Y1)2 + (X2–X1)2
Sub ÷ четыр()
‘макрос четырех’ записан 01.02.2009 ()
j = 10
k = 10
i = 10
For j = 10 To 85
For k = 10 To 85
lkv = (Cells(k, 7).Value – Cells(j, 5).Value) ^ 2 + (Cells(k, 8).Value – Cells(j, 6).Value) ^ 2
If (lkv > = 0.72) Then GoTo 10
GoTo 5
10 If (lkv < = 0.74) Then GoTo 155 Next k
Next j
GoTo 2015 Cells(i, 11).Value = lkv
Cells(i, 12).Value = k
Cells(i, 13).Value = j
i = i + 1
GoTo 5
20 End Sub
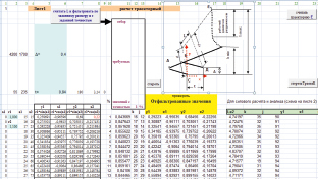
Рис. 1.2. Элементы алгоритма
Это выражение насчитывается, например, для 90 значений углов поворота рычага r1 исходя из введённой таблицы. Точность расчета механизма можно увеличить, если шаг расчета для углов уменьшить, например, до 0,1°. Т.е. для 900 значений угла. Расчёт L2 производится в программе VBA (меню «сервис – макрос», см. текст макроса).
В нём после расчёта величины L2 производится её анализ и значения, удовлетворяющие условие 0,73 >= L2 >= 0,72 (это принятая длина L2), отправляются в соответсвующий столбец К. Значение соответствующих углов наклона рычага r1 а1 рычага r2 а2 соответственно в столбцы L и K (рис. 5 и 4). Понятно, что задавая меньшие значения L2, например, 0.73 и 0. 725, можно как угодно поднять точность вычислений (конечно и уменьшая шаг углов). Чем выше заданная точность, тем меньшее количесво значений, удовлетворяющих условию, будет найдено программой. Запуск макроса осуществляется кнопкой на рис. 1.2. Заметим, что расчет L2 с учётом того, что связь между углами ведётся для всех возможных комбинаций сочетаний а1 и а2. Иначе говоря циклы операторов for организованны так, что значению а1, например, 15°. выбирается а2 – 15°, затем ему же – 16°. Затем ему же 17°. и т. д. до 90°. После чего а1 придается значение 16°, а значения а2 вновь повторяются от 15 до 90°. И т. д. пока не будут насчитаны все 90*90 = 8100 значений, из которых и выбирается требуемое L2, заносимое в столбец К. Интерфейс программы легко приблизить к тем, которые используются в вышеперечисленных ПО, например, используя диалоговые функции типа IputBox(), для внесения исходных данных. В исходном ПО (Autocad) используется язык Lisp, в ANSYS Fortran, но большой разницы в использовании языков нет, тем более, что в этом фрагменте используется небольшое количество операторов языка (4) и наиболее популярный алгоритм цикла и выбора данных, применяемый во многих случаях программирования, знание которого обеспечивает решение достаточно сложных задач. Поэтому цели моделирования могут быть успешно достигнуты.
Далее имея достаточное количество табулированных положений механизма, где все его параметры соответственны, можно получить аттрактор его любой точки. Для этого достаточно использовать уравнение прямой проходящей через две точки, которое для рассмотренных условий выглядит так:
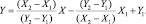 (1.1)
(1.1)
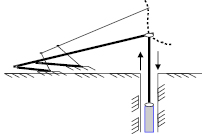
Рис. 1.3. Шарнирно соединённые элементы четырёхзвенника, закрепленные к основанию (заштрихованные элементы)
Подставив в (1) значение точки Е, получим траекторию движения верхняка крепи, если таковым рассматривать данный четырехзвенник. Программа позволит оптимизировать лемнискату Е таким образом, чтобы в рамках рабочего хода механизма лемниската была максимально близка в вертикальной. Имея текст программы и понимая её алгоритм, студент легко определит и возможности оптимизации за счет изменения параметров r1, r2, L, t, Δ.
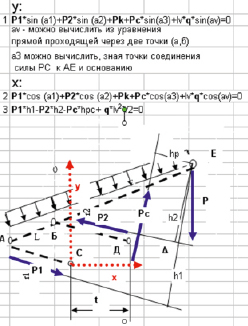
Рис. 1.4. Расчетная схема для анализа
Далее приведено выражение для 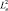 как сумма квадратов соответствующих разницы координат, образующих катеты прямоугольного треугольника.
как сумма квадратов соответствующих разницы координат, образующих катеты прямоугольного треугольника.
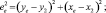 (1.2)
(1.2)
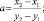 (1.3)
(1.3)
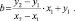 (1.4)
(1.4)
Соединение этих уравнений позволяет получить хе – горизонтальную проекцию крайней точки Е.
Уравнения прямой проходящей через две точки:
у = а∙х + b.
Коэффициенты а и b определить в соответствии с (3) и (4) формулы внесены в таблицу, где их значения для 85 положений механизма рассчитаны. Квадратное уравнение, определяющее квадрат отрезка от точки 2 до крайней точки Е коромысла.
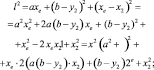
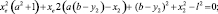
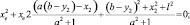
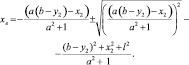
Это позволяет определить оптимальные параметры для рассматриваемых устройств, например, для станка – качалки следует иметь диапазон траектории механизма, где крайняя точка корамысла осуществляет движение близкое к вертикальному. Графики движения по расчётным положениям механизма через 1 градус показывают, что это осуществимо.
На рис. 1.4 представлена схема для проведения силового анализа механизма.и основные уравнения, связывающие параметры сил и геометрии механизма.
Сила Рс моделирует действие гидростойки, которая привязана к конкретным точкам ограждения и основания. Табулирование траектории точки крепления стойки к ограждению также производится на основе (1). Напомним, что после завершения выбора геометрических параметров крепи и получения столбцов данных K, L, M они используются для силового анализа (определения сил Р1, Р2, Р для положений механизма).
Замечание. Предложенная авторская методика применима к классу задач, связанных с оптимизацией четырёхзвеников и выбору параметров механизированных крепей для обеспечения параллельного движения козырька крепи при просадке её гидростоек.
Как было установлено, сочетание технологий Adams с авторским программами позволяет расширить возможности пакета, в частности, на основе представленной выше программы оптимизировать размеры лемнискатного механизма проще и быстрее по времени в 2–3 раза. Это связанно с громоздкостью проектирования с помощью примитивов пакета, когда для ускорения решения необходимо использовать кодирование на достаточно сложном языке при отсутствии литературы для этих целей. Графики на рис. 1.6, полученные при введении исходных данных и нажатии клавиши рис. 1.2 «Считать траекторию» это демонстрирую.