
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ПРОГРАММИРОВАНИЕ, УПРАВЛЕНИЕ И ЦИФРОВЫЕ МОДЕЛИ ЗАБОЕВ ГАЗОУГОЛЬНЫХ ШАХТ
Жетесова Г. С., Бейсембаев К. М., Нокина Ж. Н., Телиман И. В.,
1.3.3. Особенности работы и микромоделирование технологических элементов работы в камере, основных деталей рештаков и става скребкового конвейера
При макроподходе объект рассматривается, снаружи (рис. 1.10), как единое целое. Для макромоделирования горных машин может рассматриваться технология, в которой работает машина, или взаимодействие узлов самой машины. В рамках рассматриваемой базовой схемы работы, поворотного конвейера это будет выполнено для камерной выемки угольных пластов. По существу макромоделирование и имитационное моделирование во многом схожи. Это взаимодействие определяет особенности внешнего нагружения машины или внешних нагрузок действующих на узлы и подузлы, углового (поворотного) конвейера. Ранее на рис. 1.9 была приведена схема работы конвейера при камерной выемке. Для макромоделирования применение пакетов Adams известно, хотя опубликованных в открытом доступе статей по данному направлению не много. В основном пакет использовался для моделирования робототехнических систем, манипуляторов, автомобилей. В нашем случае, задача моделирования распадается на несколько частей: моделирование всей базы конвейера с учетом взаимодействия с зоной установки и моделирование движения скребков по рештаку в зоне поворота. Здесь конвейер следует за проходческим комбайном, разворачиваясь в зоне 5, и при некоторых условиях можно однозначно определить его положение.
Изучение Adams показывает, что такие задачи с трением следует тшательно изучать и тестировать. Одна из расчетных схем на рис. 3.5. Здесь, считаем что рештаки подвижны и представляют собой шарнирные балки на шарнирных опорах. Нагрузка из модели Адамс для опорных зон взаимодействия скребков с бортами рештаков. Задача макромоделирования сводится к взаимодействию скребков с рештаками в зоне поворота. Считаем, что здесь скребок прижат к борту, ближнему к центру поворота и связь с бортом можно моделировать ползунным механизмом. Но поскольку скребок может поворачиваться относительно борта, эту связь производим через дополнительный элемент, который и называем ползуном, соединяем его со скребком поворотной шарнирной связью. Тогда противоположный конец можно считать свободным от внешних связей. На рис. 1.11 схема расчета става поворотного конвейера и её упрощение за счет линеаризации задачи, одновременно показан в аналогичных положениях и макет поворотного узла изготовленный на КарГорМаш-М и подтвердивший адекватность теоретических предположений и работоспособность конструкции. Макет в среднем сечении имеет полость созданную верхним и нижним средними листами и поворотные секторы расположены внутри полости, что предотвращает их цепляние ветвью холостого хода. Показано положение при повороте на 60° и прямолинейное. В этом случае став можно моделировать много пролетной балкой на шарнирных опорах, а затем перейти к расчету максимально нагруженной пары соединенных рештаков, когда может быть использована полная цифровая модель рештака, со всеми конструктивными особенностями в представимых типоразмерах. Как показывают расчеты прочность става при выполнении параметров по разработанному макету будет обеспечена (рис. 1.12, 1.13). При расчете цифровой модели с шарнирным опиранием по крайним проушинам двух связанных шарниром вращения (пальцем) рештаков установлена форма деформации рештаков и получены рекомендации к проектированию. Выявлена и необходимость строгого выполнения заданных режимов движения тягового органа и на холостой ветви, получена возможность расчета расстояния, между средними листами рештаков обеспечивающего жесткость става и максимальным давлением скребков при их подходе в зоне стыков рештаков. Показано, что прочность учетом рис. 1.14–1.17 обеспечивается. Расчёт усилий, в узлах, скоростей и ускорений при движении скребков и цепи основан на решении систем уравнений равновесия, для опорных реакций в узлах и может быть реализован в системе Excel [32], где применяется технология языка VBA, а также на основе известного пакета авто проектирования ADAMS. Его применение в КарГТУ и других организациях для углового конвейера малоизвестно. Ещё меньше сведений о сопоставлении, полученных на его основе результатов с практикой. Модели оборудования будем собирать из твёрдых тел, соединений (шарниры вращения и поступательного движения) и силовых факторов. Предварительно рассмотрим упрощенную схему модели, когда зона поворота представлена в виде дуги окружности (рис. 1.18).
Исходя из геометрии проекция силы на ось Y, действующей на скребок с номером n в шарнире соединения цепей со скребком справа от О2:
Fny = Fn∙sin ((90° + θ) /2 – αn), (1.11)
силы сопротивления части груза G0 на скребке и самого скребка при коэффициенте трения fтр. В направлении к центру поворота от центра массы О2 скребка и груза, приходящегося на него действует сила инерции определяемая вращаением с линейной скоростью v:
Рyi = mпр∙(ds /dt)2 /R2. (1.12)
Его смешению препятствует сила сопротивления Fтрi направленная к центру вращения, которую можно приближенно определить через вес G0 и коэфициент трения fтр. При существующей скорости транспортирования угля из лавы величина силы инерции будет не значительной. В решении неучитывается и трение торца самого скребка о рештак в месте опоры, хотя предполагаем, что прижимающее усилие при небольшом количестве рештаков и длине лавы около 200 м может быть существенной.
Fтр.y = G0∙fтр∙sin (90° – αn), (3.13)
для силы тяги скребка слева от шарнира О2:
Fn′y = Fn′∙sin ((90° – θ) /2 – αn). (3.14)
Рис. 1.10. К основным уравнениям макромоделирования

Рис. 1.11. Схема расчета как многопролетных балок: а: 1 – шарнирные опоры; 2 – опорные реакции скребков; 3 – шарниры соединения; б – упрощенная схема расчета: 4, 5 – шарниры поворотных стяжек; 6 – шарниры соединения рештаков; 7 – стяжка
Тяговое усилие:
F = x1 + x2 + ... + xn + F′; (3.15)
F = y1 + y2 + ... + yn + F′, (3.16)
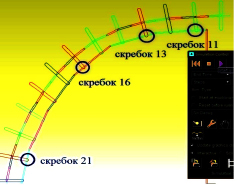
где F′ – часть тягового усилия для приведения в движение прямолинейной части конвейера. Сумма проекций сил действующих на скребки участвующих в повороте на оси Х и Y, а также сумма моментов, например, относительно точки О1 составленная для каждого скребка в общем случае определит выражения для VBA в Excel. В результате определяется нагруженность бортов рештаков и скребков на повороте, что позволит улучшить надёжность проектирования конвейера. Аналогичная задача, но с возможностью конкретизировать конструкцию условиям работы представлена в пакете ADAMS, где рассмотрена группа рештаков, осуществляющих поворот, группа моделируется элементами (Link) в количестве 3–13 штук (рис. 1.19 – симуляция движения), прикреплённых неподвижно к «земле» (ground) секций по поверхности которого движутся скребки по три на рештак. Скребки своим внутренним концом – опорой, контактируют с гранями элементов моделирующих борта рештаков. Движение элементов рассматривается только в пределах каждого рештака, но поскольку они кинематически связаны через модель цепи, то учитывается полная группа рештаков в зоне поворота. Проектирование и испытания модели целесообразно начинать с создания минимального количества скребков, которые затем доводим до полного, что позволяет выявить особенности влияния, на характер движения конструктивных решений, включая неточности компоновки деталей. Скребки находятся в неустойчивом состоянии, поскольку сила тяги приложена к центральной точке возможного вращения скребка, опорные реакции в точках контакта с рештаком направлены по оси скребка и эти факторы не препятствуют колебаниям относительно шарниров. Создание всей поворотной системы не приводит к качественным изменениям в нагрузках.
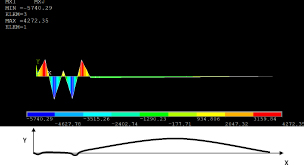
Рис. 1.12. Картина нагружения става: а – изгибающие напряжений; б – картина деформаций
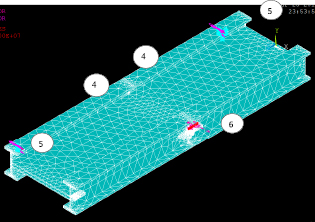
Рис. 1.13. Схема соединения рештаков в макроцифровой модели: 4, 5, 6 – совпадают с позициями на рис. 3.12
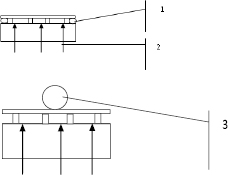
Рис. 1.14. Для оценки напряжений в рештаке: 1 – контактные шарниры; 2 – опорные реакции; 3 – низкомодульное колесо
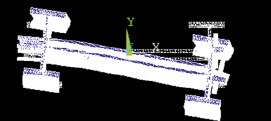
Рис. 1.15. Характер деформации и опасные зоны сечения
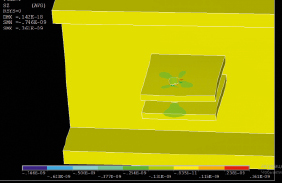
Рис. 1.16. Картина нагружения зоны шарнирного соединения рештаков
Графики опорных усилий при движении скребков под действием тяговой силы имеют периодический характер. Для некоторых скребков имеем значения усилий изменяющих знак, что объясняем колебаниями бȯльшей чем на остальных амплитудах. Моделирование полной зоны поворота показывает, что проекции опорных усилий изменяются от максимума к минимуму и наоборот на каждом скребке. По длине зоны поворота проекции усилий на ось Х изменяются от минимума в зоне разгрузки конвейера до максимума в зоне привязки линейной части конвейера. При этом подходе в зоне стыка состояние скребка отличается от остальных.
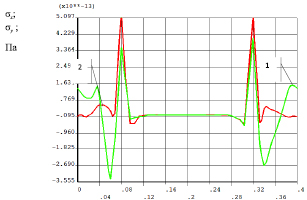
Рис. 1.17. Графики нагружения рештаков: а – напряжения вдоль планки соединения рештаков: 1 – σх; 2 – σу
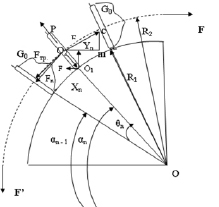
Рис. 1.18. Идеализированная схема нагрузки на поворотные рештаки
Установив элементы и приемы моделирования по пакету Adams стало возможным уточнение элементов движения деталей с учетом их фактически ускоренного и в среднем равномерного движения. При работе скребкового конвейера движение цепи, пульсирующее даже при постоянной скорости вращения звездочки, что связано с изменением мгновенного радиуса набегания цепи, а также вследствие неравномерного характера транспортирования груза. Для приводной массы конвейера mk, диаметра звездочки D – передаточного отношения up, углового ускорения ε среднего пускового момента двигателя, статического приведенного к двигателю момента Мс, и приведенного к двигателю момента инерции всех движущихся масс Jпр усилие в цепи:
Sд.п = mk·D·ε / (2up), (3.17)
ε = (Mп.ср – Мс) /Jпр (3.18)
в ряде случаев удается замерить усилия на головной и концевой звездочках получить графические зависимости их изменения. В среднем, считая изменения тягового усилия цепи при переходе от участка к участку линейным и его можно рассчитать, а полученные значения использовать при моделировании. При этом для различных случаев нагружения и особенностей работы программу раcчета следует подготовить с возможностью изменения этих данных в широких пределах. В ряде случаев рассматривают равномерное движение тягового элемента и груза. При этом учитывают, что в этом случае удается упростить системы уравнений и построение модели. Геометрические размеры на рис. 1.20.
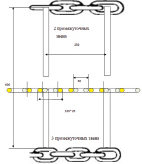
Шаг цепи определяет количество лучей звездочки и основные размеры средней части скребка – ушка, которая может цепляться зубом звездочки. Также как и в обычных конвейерах, ушки скребка и есть звено цепи. И она крепиться к скребку так, что бы произошло зацепление со звездочкой. Здесь приведены два варианты для моделей, когда скребки соединены двумя промежуточными звеньями цепи и тремя.
На рис. 1.21, 1.22 представлены параметры модели (фото с экрана приложения Адамс) и в начале можно рассматривать движение с момента, когда начальная скорость скребков равна 0. Вращение приводной звездочки происходит с постоянной скоростью и движение цепи равномерное после того, как произошло ускорение от 0 до некоторой окружной скорости. В начале можно рассмотреть движение, когда цепь сложена в бухту и на последний элемент наложено усилие натяжения f2, а на первое звено f1. На правые концы скребков наложены, направленные вниз возмущающие нагрузки f3, f4, f5, которые имитируют силу трения скребка о рештак или некоторое возмущающее равновесие усилие, например односторонний перегруз скребков. Моделирование в такой постановке позволяет определить возможные параметры разгона скребков, а затем перейти к задаче равномерного движения. При этом очевидно, что сумма усилий на ось Y при отсутствии ускорения должна быть равна 0.
а б
в
Рис. 1.19. Поэлементное моделирование движения скребков: а – перед началом движения; б – в конце движения; в – полная компоновка; 1 – скребок; 2 – элемент связи скребков; 3 – борт рештака; 4 – направление силы тяги; 5 – связь линейного шарнира; 6 – шарнир вращения элементов связи скребков
а
б
Рис. 1.20. Схема расположения цепи относительно скребка: а – размеры; б: 1 – скребок; 2 – ушко; 3 – промежуточное звено; 4 – жесткая связь скребка и ушка; 5 – шарнирная (вращательная) связь
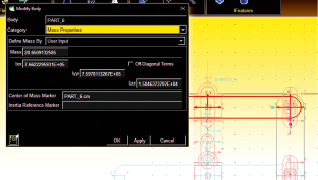
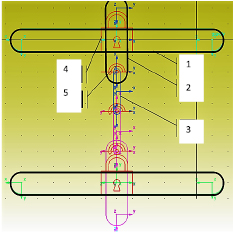
Рис. 1.21. Окно ввода данных
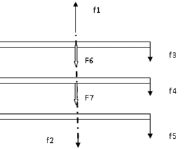
Рис. 1.22. Схема расчета
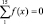 (3.19)
(3.19)
или F1 – f2 + (F3 + F4 + F5)∙3 + f6 + f7 + f8 = 0.
Последовательно увеличивая количество скребков можно установить их влияние на параметры движения.
Вначале рассмотрено движение скребков на прямолинейном участке, но и в этом случае можно оценить влияние конструктивных параметров скребка на возможности колебаний. Так действие силы трения или иноговозмущающего усилия на один из торцов скребка вызывает его угловое смещение, но этому препятствует возникающий при повороте скребка момент от пары сил, возникающих со стороны передней и задней части конвейера на ушки скребка в точках крепления цепи. И чем больший поворот скребка, тем больший восстанавливающий момент действует в системе. Заметим, что в окне ранее представленного рис. 1.21 показаны динамическая характеристика скребка: массы, осевые моментов инерции.
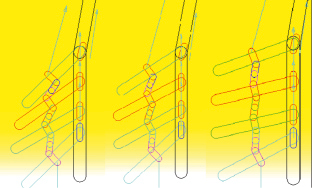
Состояние Userinput позволяет изменить эти значения прямым вводом. При натяжении 400 н наклон меньше (а), при 1000 еще меньше, заметно влияние на последний (верхний скребок) (б). Для положений «а» и «б» груз весом не моделировался и вес скребка 20, 65 Н. На рис. 1.24, 1.25 представлены возможности введения сил натяжения и получения графиков усилий в шарнирах (с номерами 20 и 21), что демонстрирует широкие возможности пакета Adams и для других параметров и элементов модели. Для рис. 1.23, 1.26 для обеспечения движения силу натяжения примем 2544 н (3566 – 1000 = 2566), силу тяги = 4566.
Возмущающая нагрузка увеличена до –280 Н.
а б в
Рис. 1.23. Особенности движения: а – натяжение 400 н; б – 1000 н; в – близкие значения усилий тяги и натяжения
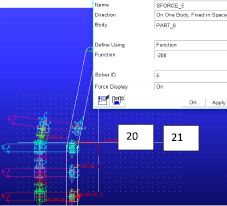
Рис. 1.24. Эксперимент с наклонным рештаком: 20, 21 – поступательный и вращательные шарниры
Судя по результатам (рис. 1.23) движение с наклонным рештаком в большей степени возбуждает автоколебания, но оно остается устойчивым особенно при возрастании силы натяжения (рис. 1.23, в).
Как следует из протокола приемочных испытаний макета поворотного узла конвейера сложности движения тягового органа возрастают при таком увеличении угла поворота рештаков в диапозоне 0, 45, 75 градусов.
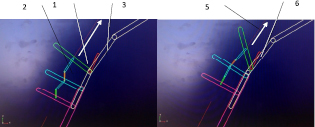
При правильной регулировке усилия натяжения цепи тягового органа винтовыми устройствами с пружинами (поворот до 45°) движение протекает плавно без явных признаков динамики. При максимальном угле около 83–90 градусов возникают ударные нагрузки и интенсивные колебания скребков. И в частности это связано с отклонением от требования при изготовлении макета, так фаски на торцах рештаков не были сняты. И при движении тягового органа в указанном диапозоне на холостой ветви происходят удары скребков об эти необработанные кромки. При углах поворота до 45 градусов зазоры между торцами рештаков непосредственно у шарниров поворота соединяюших скребки не превышают ширины скребка и поэтому ударов не происходит. Но при больших углах и относительно небольшой скорости движения цепь холостой ветви провисает и скребки со стороны зоны раскрытия рештаков проваливаются в зазоры, вызывая соударения, торможение, что повышает величину необходимого крутящего момента. При подходе скребка к стыку рештаков опорное усилие возрастает и соответственно сила трения скребка о борт, что вызывает наклон скребка, который в последующем движении выпрямляется (рис. 1.26).
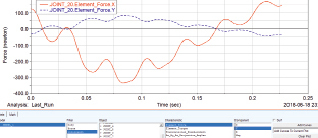
Рис. 1.25. Эксперимент для сил натяжения и тяги 2000 и 4566 Н
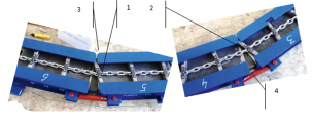
Рис. 1.26. Положение скребков тяглвого органа конвейера в зоне стыка рештаков (фото из фрагментов один момент времени движения тягового органа конвейера): 1, 2 – скребки в наклонном положении; 3 – шарниры вращения соединения рештаков; 4 – стяжки привода для поворота рештаков
Для надежной фиксации этих случаев следует обеспечить жесткое крепление скребков к звеньям цепи, что выполнено за счет предельного уменьшения зазоров и создания возможности прижатия пластины крепления к звену винтами.