
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ПРОГРАММИРОВАНИЕ, УПРАВЛЕНИЕ И ЦИФРОВЫЕ МОДЕЛИ ЗАБОЕВ ГАЗОУГОЛЬНЫХ ШАХТ
Жетесова Г. С., Бейсембаев К. М., Нокина Ж. Н., Телиман И. В.,
3.3. Программирование моделей точности взаимодействия машин и пород в недрах
Проблемы моделирования и программные ошибки. Скважинные методы добычи и воздействия на горный массив предполагают взаимодействие элементов машин с породами и полезными ископаемыми. Так, буровое устройство в скважине используется для установки обсадной крепи распираемой в породы, а непосредственно у забоя может иметь гидро- или пневмоопоры, которые выполняют функции передовой крепи или управления направлением бурения. Моделирование взаимодействия горных машин и рабочей среды требует особой точности расчётов. Модели таких систем сверхъемкие, имеют зоны для исследований, размеры которых отличаются в сотни раз и представляют собой комплекс взаимодействующих программных объектов для описания сдвижений пород, выработки, секций крепи, разрывов между участками забоя у нарушений. Точность расчетов определяется факторами, основная часть которых приведена на рис. 3.2. Краевые ошибки обычно связаны со значениями данных, используемых на границах рассматриваемых процессов. Незаметные в других областях, там они резко усиливают своё влияние, взаимодействуя с областями перехода. Используемые пакеты моделирования основаны на методе конечных элементов (МКЭ – Ansys), а также на линеаризации уравнений динамики – Adams. Они применяются в основных отраслях промышленности, однако не все аспекты их кодирования известны так же, как подробности алгоритмов рассчитываемых процессов, например, построения траекторий трещин. Поэтому исследования для получения «тонких» факторов проводятся на основе своих разработок, а профессиональные пакеты используются в объемах, допустимые границы которых установлены по результатам исследований применимости.
Особенности управления и моделирования нестационарными системами. Задачи геомеханики характерны нестационарностью результатов – поэтому в этих системах определение НДС на основе только теоретической упругой модели в принципе не возможно, а возможно в режиме обратной связи с использованием нескольких расчётных моделей, действующих на некоторых интервалах движения машин и в частности крепей. Идеология этого подхода была приведена в патенте авторов № 1833471, СССР от 07.08.93 и в [15, 17]. Она основана на бифуркационном (многозначном) характере поведения недр, что подтвердилось и для данных пород месторождений нефти и газа. Реализованные модели после накопления повреждений давали картину внезапного роста напряжений. Это можно было объяснить падением точности расчётов в рассматриваемых зонах и проявлением факторов, связанных, например, с накоплением критического уровня повреждений в отдельных узлах, когда система или узел внезапно изменяет форму деформации и, соответственно, НДС. Как оказалось, в сложных системах эти факторы проявляются совместно и требуют резкого повышения точности вычислений. В [8–9, 11] приведено статическое решение задачи, и чем больше моделируемых связей между объектами системы, тем локальней изменение формы при разрушении одной из них. Энергия деформации также изменяется не намного, но по мере достижения критического уровня освобождений от связей создаются возможности глобального изменения формы и энергии системы. В этом случае все действия претерпевающей изменение значительной части системы приходятся на ограниченную зону, что вызывает в ней резкий рост напряжений. Таким образом, и статический подход к расчёту напряжений «подводит» к моменту, когда в теле готовы начаться динамические процессы.
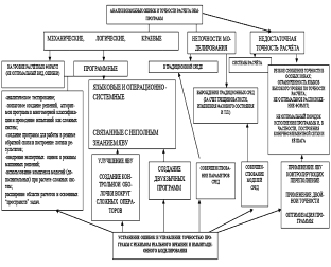
Рис. 3.2. Основные ошибки в программах и моделях
В горном массиве построение траектории трещины имеет особенности, т. к. в нём выражены три вида формоизменения: трещины вдоль и поперек напластования, а также скачкообразное сжатие участков пласта. Для определения конкретного вида разрушения на текущий момент следует установить приоритетный. То есть вычислить формоизменение, наиболее близкое к осуществлению (на которое в текущих условиях будет затрачена минимальная энергия). Программная реализация приоритетного механизма предусматривает существенное упрощение задачи за счёт рассмотрения достаточно коротких участков трещин отслоения, длина которых заранее ограничена (шаг закрепления или размер конечного элемента) и не превышает длину трещины, которая могла быть в реальности. Реализация приоритета формоизменения заключается в установке в расчетной схеме обновленных граничных условий, связанных с потерей текущей связи. Далее вновь продолжается решение и в механизме сравнения энергетических возможностей формоизменений достигается очередной приоритет, который может продолжить текущий процесс или начать новый. Программа создана так, чтобы к ней для проверки можно было привязать разные гипотезы разрушения, но количественные результаты должны координироваться режимом обратной связи с массивом. В каждый текущий момент существуют зоны, где расчеты по принятым положениям о разрушении показывают превышение их оценочных критериев на формоизменение. Приоритет допустимо оценивать уровнем превышения действующего критерия над предельным, и чем он выше, тем выше приоритет. В первых расчётных экспериментах длина отслоения участков устанавливалась исходя из шага закрепления слоёв породы, а при поперечном – учитывалось разрушение по всему сечению слоя. Осадки пласта рассматривались для участка пласта, кратного захвату комбайна (наблюдать которые можно и визуально с выработок оконтуривающих лаву). При применении метода конечных элементов, как и для отслоений, разрушение поперек напластования можно моделировать короткими участками, рассматривая медленно распространяющуюся поперечную трещину, с чередованием с другими формами разрушения. Это позволяет изучить различные состояния массива расчетом и получить их определяющие признаки при натурном разрушении. Само понятие моделирования уже обеспечивает неопределённость получаемого знания и можно говорить о степени точности соответствия натуры и модели (которую можно установить экспериментально при наличии большого практического опыта).
Т = Тн_м·Т0, (3.1)
где Тн_м – соответствие натуры и модели, причём его значение всегда меньше 1 и выражает факт, что знание относительно; Т0 – обычно используемая точность расчёта, определяемая хорошо известными компонентами.
Составление программы для обработки программного массива (матрицы или определителя) сводится к устранению повреждений и перезаписи строк и столбцов, что обычно приводит к уменьшению его ранга. Программирование таких задач можно свести к упорядоченному применению операторов цикла с обеспечением заданных условий для анализа строк и столбцов и перезаписи обновлённой матрицы. Алгоритмирование такой работы позволяет уменьшить количество ветвлений, снизить коэффициент сложности программы [38].