
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.3.4. Коэффициенты активности
Электростатические взаимодействия приводят к значительным отклонениям в поведении системы от идеального. Учесть отклонения от идеального, т.е. предусмотреть влияние электростатических факторов можно с помощью метода активностей: вместо концентраций реагирующих частиц [A] используют величины, называемые активностями aA. Численные значения активностей выбирают таким образом, чтобы форма функциональной зависимости для свободной энергии
GA = GA0 + nRT·ln[A]
сохранялась и для реальных растворов:
GA = GA0 + nRT·ln aA.
Следовательно, активность - это та концентрация, которую имел бы компонент воображаемого идеального раствора, обладающего теми же термодинамическими свойствами, что и данный реальный раствор и имеет размерность (моль/л).
Тогда для общей реакции
aA + bB = cC + dD
с учетом активностей получаем константу равновесия - выражение закона действующих масс:
K0 = aCc·aDd/aAa·aBb,
применимое к любым химическим системам - как идеальным, так и реальным.
Отношение активности частицы к ее равновесной концентрации
gA = aA/[A]
называется коэффициентом активности. Коэффициенты активности ионов в растворах электролитов могут служить мерой электростатических взаимодействий в системе. Для идеальных растворов электростатические взаимодействия пренебрежимо малы, активности приравниваются равновесным концентрациям, тогда g = 1.
Известно несколько методов определения и расчета коэффициентов активности. Поскольку электростатические взаимодействия весьма заметны в растворах электролитов, то остановимся на расчетах коэффициентов активности ионов. Они зависят от ионной силы, вычисляемой по известному уравнению:
I = (1/2)·S[Ai]·zi2,
где zi - заряд иона Аi; S - cумма всех ионов, присутствующих в растворе. Ионная сила учитывает электростатическое влияние всех ионов в растворе. Она имеет размерность концентрации и для растворов сильных I-I электролитов численно равна ей.
Одним из наиболее применяемых методов определения коэффициентов активности индивидуальных ионов является оценка по приближению Дебая-Хюккеля [8]
lggi = -Azi2(I)1/2
в случае, когда I £ 0.01 M, и
lggi = -Azi2(I)1/2/[1+aB(I)1/2],
если I = 0.01-0.1 M, где A и B - константы, зависящие от температуры и диэлектрической проницаемости растворителя (для воды при 298 К А » 0.5 и В » 0.33); а - эмпирическая константа, учитывающая размеры ионов и характеризующая среднее расстояние сближения сольватированных ионов в предположении, что они являются жесткими сферами. Значение а можно приближенно было принято считать постоянным, не зависящим от природы иона и равным ~ (3…5)×10-8 см (хотя с этим трудно согласиться).
В разбавленных растворах (I < 0.1 M) коэффициенты активности ионов меньше единицы, но при I ® 0 величина gi ® 1. Растворы с очень низкой ионной силой (I < 0.0001 M) можно считать идеальными. При высоких ионных силах коэффициенты активности начинают зависеть от природы ионов, а затем и от общего состава раствора. В этих случаях для нахождения коэффициентов активности следует пользоваться конкретными справочными данными. В очень концентрированных растворах (ионная сила больше единицы) коэффициенты активности ионов могут быть намного больше единицы. Причиной этого считается связывание значительного количества растворителя в результате сольватации ионов и, таким образом, в увеличении кажущейся концентрации ионов. При ионных силах от 0.1 до 0.5 М во многих случаях хорошие результаты дают расчеты по уравнению Дэвиса [9]:
lggi = -Azi2(I)1/2/[1+aB(I)1/2]+ CI,
где а и С - константы (подбирают эмпирически для каждого конкретного электролита).
Экспериментально определить коэффициенты активности отдельных ионов невозможно, так как нельзя получить раствор, содержащий ионы только одного сорта. Опытным путем можно было измерить лишь средний коэффициент активности g± ионов электролита AmBn, который связан с коэффициентами активности составляющих его ионов An+ и Bm- следующим образом:
g± = (gAm· gBn)(m+n).
Уравнения Дебая-Хюккеля и Дэвиса пригодны в первом приближении и для расчетов коэффициентов активности незаряженных молекул (неэлектролитов). В этих случаях zi = 0 и в уравнениях Дебая-Хюккеля коэффициент активности неэлектролита равен единице при ионной силе I £ 0.1 М, при больших значениях ионной силы необходимо использовать уравнение Дэвиса, которое для неэлектролитов превращается в lgg = CI. Константа С в этом случае называется солевым коэффициентом, зависящим от диэлектрической проницаемости неэлектролита e. Для веществ с низкойe (газы, сахара, белки) C>0, g > 1. Для таких веществ наблюдается эффект “высаливания”, т.е. уменьшение их растворимости в воде в присутствии электролитов. Для веществ же с высокой e(например, для HCN e = 111) C< 0, g < 1.
Все, что было сказано выше, свидетельствует о непростой ситуации с коэффициентами активности как гидратированных или сольватированных ионов, так и нейтральных молекул (неэлектролитов), для которых до сего времени не было разработано единой, всеохватывающей теории, позволяющей однозначно рассчитывать g. Допускается неоправданно большое число подгоночных параметров при изменениях концентраций одного и того же растворенного вещества и природы растворителя.
Теория гидродинамических флуктуаций в растворах симметричных и несимметричных, сильных и слабых электролитов, предлагаемая нами, дает возможность оценивать коэффициенты активности и отдельных ионов, и недиссоциированных молекул, а также транспортные свойства во всем диапазоне изучаемых концентраций (от 0 до 4-5 моль/л) в любом растворителе.
1.3.4.1. Соотношения между коэффициентами активности и концентрацией растворов электролитов
Коэффициент активности есть мера отклонения реальных (практических, экспериментальных) параметров от идеальных, разработанных в первом приближении для разбавленных растворов неэлектролитов. Величины их в растворах высоких концентраций становятся виртуальными. В самом деле, значения коэффициентов в несколько десятков, то есть отклонений от идеальных параметров в десятки раз, сложно приспособить к законам для практического применения в растворах, где доминируют процессы ассоциации или других межмолекулярных взаимодействий.
Тем не менее, имеется ряд фактических данных о зависимости коэффициентов активности электролитов от моляльности, причем при некоторых концентрациях (от децимоляльных для одних электролитов до нескольких моляльностей для других) наблюдается точка минимума.
До сих пор в литературе нет внятных объяснений и, тем более, обоснований появления этого минимального значения коэффициента активности.
По нашему мнению [10, 11], коэффициенты активности представляют собой вероятность распределения ионных составляющих растворов по Больцману, которая применительно к растворам может быть аппроксимирована следующим образом:
g = exp(-ћw/kБT) (1.22)
g = exp[-(4pzKtzAne2ћ2CiNA/m·1000· kБ2T2)1/2] (1.23)
где w - частота плазмоподобных колебаний «диссоциация-рекомбинация в нейтральные молекулы или ионные ассоциаты» (а) в растворах электролитов [12]
![]() , (а)
, (а)
w = (4pzKtzAne2CiNA/m·1000)1/2;
ћ - постоянная Планка;
zie - заряд иона;
Ci - ионная составляющая электролита (Сi = С·a, С - исходная концентрация электролита, a - степень диссоциации электролита);
NA - число Авогадро;
m - приведенная масса несольватированных ионов электролита, определяемая по формуле: m = 1/mKt + 1/mAn;
kБ - константа Больцмана;
Т - температура по Кельвину.
В данной работе предложено модельное уравнение расчета оптимальных концентраций электролитов, соответствующих минимуму коэффициента активности и рассуждения [13-18].
Показано, что в точке минимума функции
g = f(C) (1.22)
при концентрации С0, характеризующей gmin имеет место равенство ћw = kБT, w = w0 и это характеризует особую точку, в которой происходит изменение знака диэлектрического отклика. При w =w0 и далее при всех w >w0 в растворе электролита образуется новая структура, элементами которой являются ионные ассоциаты. В этой особой точке коэффициент активности g имеет минимально возможное значение. Чтобы сшить решения до и после равенства ћw = kБT , сокращая показатель экспоненты и учитывая универсальные постоянные, приходим к виду:
g = 0.368·exp[-(245.467/T)·(C0/μ)1/2] , (1.23)
а затем − к выражению (4):
g = 0.368·exp{[(C0)1/2-(C)1/2]/(C0)1/2} (1.24)
где С0 - концентрация электролита в точке gmin.
Из уравнений (1.22), (1.23) и (1.24) подстановкой универсальных постоянных и размерности в СГС: kБ = 1.38·10-16, е = 4.8·10-10, ћ = 1.05·10-27, NA = 6.023·1023, масса в ед. СГС равна 1.67·10-24, получаем:
![]()
С0 = 1.02·10-6·m·Т 2/ ![]() (1.25)
(1.25)
Уравнения (1.23) и (1.24) выражают коэффициент активности для неассоциированных ионов электролита, тогда как литературные (экспериментальные) величины g± учитывают в этой точке фактические (реальные) взаимодействия сольватированных ионов с образованием молекулярной формы электролита или ионных ассоциатов по равновесию (а). Поэтому не следует ожидать полного тождества коэффициентов активности, теоретически оцененных по уравнению (1.24), с литературными, но, безусловно, важен характер зависимости коэффициентов активности от концентраций.
В табл.1.3 приведены полученные концентрации для 42 электролитов при gmin.
Таблица 1.3
Значения концентрации электролита C0, моль/л при gmin по уравнению (1.25)
| Ион | Li+ | Na+ | K+ | Rb+ | Cs+ | NH4+ |
| F- | 0.46 | 0.94 | 1.16 | 1.41 | 1.51 | 0.84 |
| Cl- | 0.53 | 1.26 | 1.68 | 2.27 | 2.54 | 1.08 |
| Br- | 0.58 | 1.62 | 2.37 | 3.74 | 4.52 | 1.33 |
| I- | 0.60 | 1.76 | 2.70 | 4.63 | 5.88 | 1.43 |
| NO3- | 0.56 | 1.52 | 2.17 | 3.26 | 3.83 | 1.26 |
| ClO4- | 0.59 | 1.69 | 2.54 | 4.17 | 5.15 | 1.38 |
| CNS - | 0.56 | 1.49 | 2.11 | 3.13 | 3.66 | 1.24 |
Что касается увеличения коэффициента активности g при больших концентрациях электролита, то не было предложено рациональной количественной теории, определяющей концентрации растворов с минимумом g и значительным увеличением его с повышением моляльности. В данной работе дается объяснение этому факту и рассчитаны оптимальные концентрации электролитов, соответствующие минимуму коэффициента активности. Так, за пределами концентрации С0, соответствующей минимуму коэффициента активности, в связи с сокращением длин свободного пробега сольватированных ионов или молекул, превалирующими становятся межионные взаимодействия, приводящие преимущественно к ионным ассоциатам в полярных с низкими значениями диэлектрических проницаемостей растворителях или к молекулярным сольватам в неполярных с низкими значениями диэлектрических проницаемостей растворителях.
Уравнение (1.24) позволяет рассчитывать теоретические значения коэффициентов активности различных электролитов в зависимости от их концентраций. Функция проходит через минимум при С0, повторяя контур зависимости фактических (реальных) g± от моляльности растворов (рис. 1.1 и 1.2).
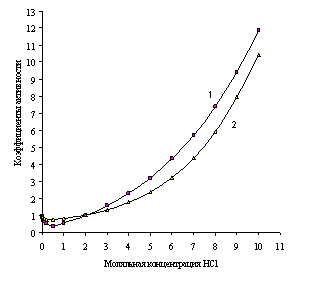
Рис. 1.1. Зависимости рассчитанных (1) и экспериментальных (2) коэффициентов активности от моляльной концентрации водного раствора хлороводородной кислоты
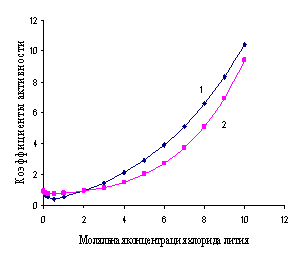
Рис. 1.2. Зависимости рассчитанных (1) и экспериментальных (2) коэффициентов активности от моляльной концентрации водного раствора хлорида лития
На рис. 1.1 и 1.2 показана приемлемость предлагаемой модельной оценки коэффициента активности в связи с достаточно заметным соответствием хода зависимости функций g = f (m) и g± = f (m) для водных растворов хлороводородной кислоты (рис. 1.1) и хлорида лития (рис. 1.2).
В табл. 1.4 в качестве примера представлены экспериментальные (литературные) и рассчитанные по уравнению (1.24) величины коэффициентов активности хлороводородной кислоты и хлорида лития.
Таким образом, в данной работе теоретически обосновываются области концентраций растворов электролитов, в которых наблюдается минимум коэффициентов активности, объясняется феномен доминирования ассоциативных явлений, приводящих к образованию ионных ассоциатов или в зависимости от свойств и природы растворителя − к преимущественному состоянию растворов в виде молекулярных сольватов.
Таблица 1.4
Коэффициенты активности HCl и LiCl, оцененные по уравнению (1.24), в сравнении с экспериментальными в зависимости от концентрации С (моль/1000 г)
| МоляльностьСm , моль/1000 г воды | HCl | LiCl | ||
| g (теор.) | g±(лит.) | g (теор.) | g± (лит.) | |
| 0.001 | 0.9565 | 0.965 | 0.9579 | 0.963 |
| 0.002 | 0.9390 | 0.952 | 0.9407 | 0.948 |
| 0.005 | 0.9051 | 0.928 | 0.9077 | 0.921 |
| 0.01 | 0.8684 | 0.904 | 0.8719 | 0.895 |
| 0.02 | 0.8190 | 0.875 | 0.8237 | 0.865 |
| 0.05 | 0.7291 | 0.830 | 0.7358 | 0.819 |
| 0.1 | 0.6396 | 0.796 | 0.6478 | 0.790 |
| 0.2 | 0.5314 | 0.767 | 0.5412 | 0.757 |
| 0.5 | 0.3679 | 0.757 | 0.3787 | 0.739 |
| 1.0 | 0.5570 | 0.809 | 0.5347 | 0.774 |
| 2.0 | 1.0006 | 1.009 | 0.9445 | 0.921 |
| 3.0 | 1.5686 | 1.316 | 1.4615 | 1.156 |
| 4.0 | 2.2914 | 1.762 | 2.1118 | 1.510 |
| 5.0 | 3.1998 | 2.380 | 2.9207 | 2.020 |
| 6.0 | 4.3273 | 3.220 | 3.9156 | 2.720 |
| 7.0 | 5.7119 | 4.370 | 5.1272 | 3.710 |
| 8.0 | 7.3959 | 5.900 | 6.5895 | 5.100 |
| 9.0 | 9.4273 | 7.940 | 8.3408 | 6.960 |
| 10.0 | 11.8596 | 10.440 | 10.4235 | 9.400 |
